利用n阶完美和幻方构造n2阶完美和幻方
张 婧,刘兴祥,刘娟娟
(延安大学 数学与计算机科学学院,陕西 延安 716000)
关于幻方的研究成果[1-10]已颇为丰富,而一种特殊幻方——完美幻方,又称纯幻方或泛对角线幻方刚刚兴起。本文在充分掌握幻方定义及性质之后,给出完美和幻方的定义,并根据完美和幻方的定义,给出了利用整数阶完美和幻方构造整数的平方阶完美和幻方的一种新的构造方法。
1 预备知识
定义1[1]设矩阵A=(aij)m×n∈Zm×n,m,n∈N*,若矩阵A满足以下条件:
①m=n;
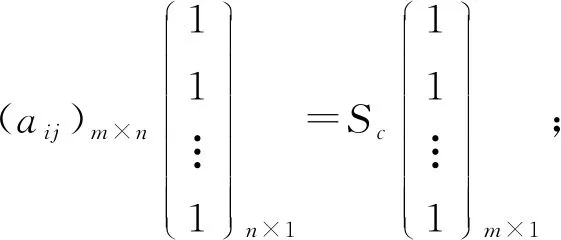
③(11…1)1×m(aij)m×n=Sl(11…1)1×n;
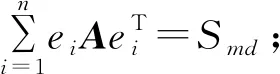
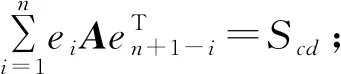
⑥Sc=Sl=Smd=Scd。
则称矩阵A=(aij)m×n为Z上的n阶和幻方,幻和记为S。
定义2[1]设矩阵A=(aij)n×n∈{1,2,…,n2},n∈N*,若矩阵A满足以下条件:

②(11…1)1×m(aij)m×n=Sl(11…1)1×n;
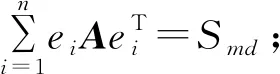
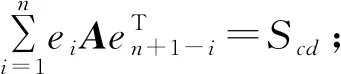
⑤Sc=Sl=Smd=Scd。
则称矩阵A=(aij)m×n为Z上的n阶始元和幻方,幻和记为S。
2 主要结论
定义3 设矩阵A=(aij)n×n∈Zn×n,n∈N*,∀u∈{0,1,…,n-1},记p≡i+u(modn),q≡n+1-u-i(modn),若矩阵A满足以下条件:

②(11…1)1×m(aij)m×n=Sl(11…1)1×n;
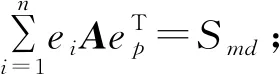
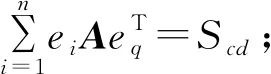
⑤Sc=Sl=Smd=Smd=Scd。
则称矩阵A=(aij)m×n为Z上的n阶完美和幻方,幻和记为S。
定义4 设矩阵A=(aij)n×n∈{1,2,…,n2},n∈N*,∀u∈{0,1,…,n-1},记p≡i+u(modn),q≡n+1-u-i(modn),若矩阵A满足以下条件:

②(11…1)1×m(aij)m×n=Sl(11…1)1×n;
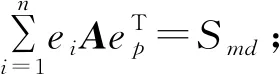
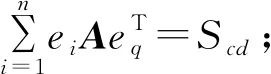
⑤Sc=Sl=Smd=Smd=Scd。
则称矩阵A=(aij)n×n为Z上的n阶始元完美和幻方,幻和记为S。
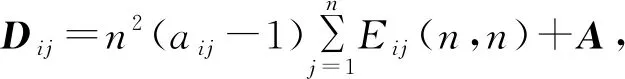
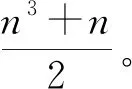
所以矩阵B是完美和幻方,且B=(bij)n2×n2∈{1,2,…,n4},则矩阵B为n2阶始元完美和幻方,证毕。
例:给出5阶完美和幻方A,构造Dij,如下:

则矩阵B为25阶始元完美和幻方,且幻和为7825。
3 小结
我们知道,单偶数阶完美和幻方不存在,所以只能用奇数阶完美和幻方构造奇数阶完美和幻方,或利用双偶数阶完美和幻方构造双偶数阶完美幻方。幻方遵循一定的规律,而完美幻方遵循更强的规律,并且在我们的生活和科研中运用很广,希望有兴趣的学者可以参与其中,使幻方得到更加广泛的应用。

