一般齐次核Hardy-Mulholland型不等式
黄启亮,杨必成,王爱珍
(广东第二师范学院数学系,广东广州510303)
0 引 言

当p=q=2时,式(1)变成著名的 Hilbert不等式。在相同条件下,还有以下具有相同最佳常数因子不等式(参阅文献[1]定理343,置换am(bn)为mam(nbn)):

则有以下Hardy-Hilbert型不等式(参阅文献[1]定理321,置换 am(bn)为 μ-1/qmam(ν-1/pnbn)):
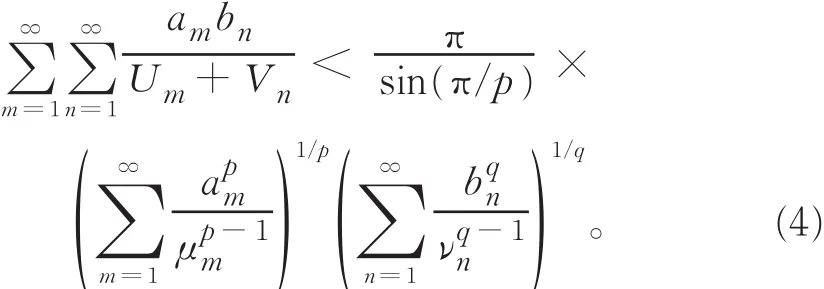
当 μi,νj≡ 1(i,j∈ N)时,不等式(4)变为式(1)。
关于式(1)及式(2)的推广应用,相关成果颇丰[2-6]。文献[7-9]给出了式(4)的引入参量的推广及加强形式。洪勇等[10]考虑了式(1)在一般齐次核推广形式下最佳常数因子联系参数的一个充分必要条件。其他涉及积分及半离散的类似工作可参阅文献[11-15]。
参考文献[10]的工作及类比式(3)和式(4),笔者运用实分析技巧、权函数方法及参量化思想,给出一个含多参数的一般齐次核Hardy-Mulholland型不等式(见引理2),此为式(2)的推广,并讨论其常数因子取最佳值时的联系参数的等价陈述(见定理2),还导出了若干应用特例(见注3及例1)。
1 权系数不等式

引理1定义权系数:

有以下不等式:
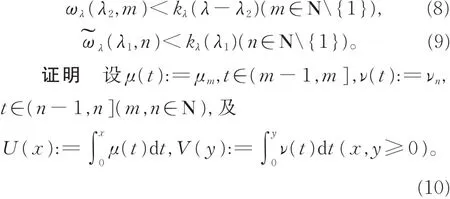
则有

因 V(y)在 (n-1,n](n∈N)严格递增,对于 λ2-y∈(n-1,n](n∈N{1})严格递减。由递减性质(参阅文献[7]引理 1),有

故式(8)成立。

2 引理及主要结果
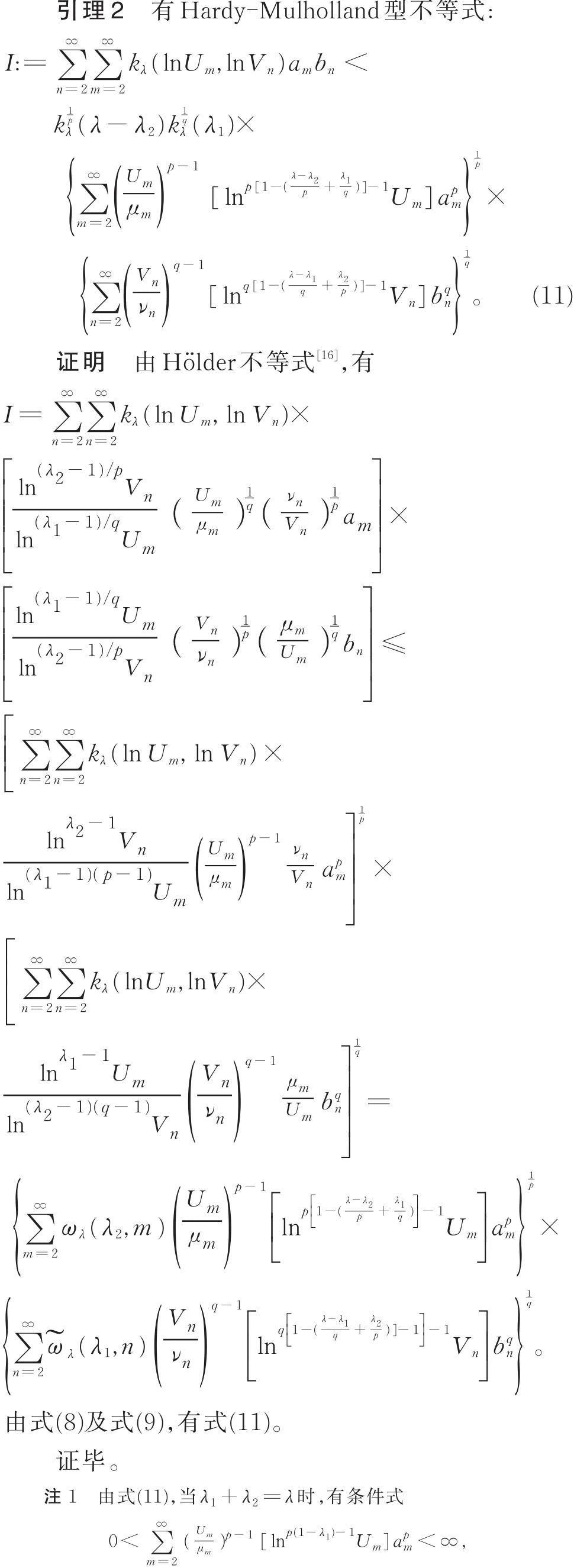

证明任给ε>0,置

若用正常数 M(M ≤kλ(λ1))置换式(12)中的常数因子 kλ(λ1),式(2)仍成立,则有

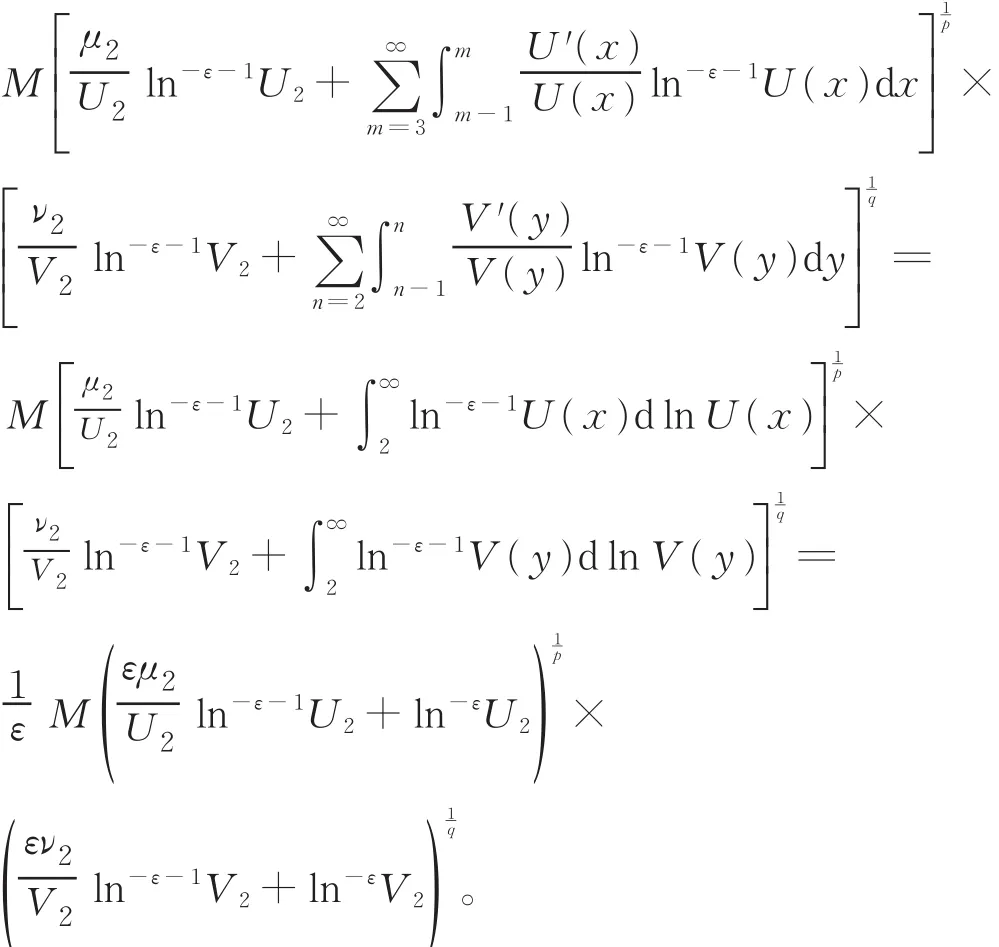
由μm≥μm+1,νn≥νn+1,递减性质及交换积分次序的Fubini定理[17],有


令ε→ 0+,由 Fatou引理[17],有
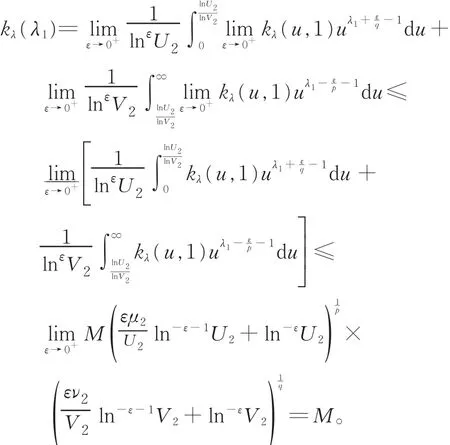
故 M=kλ(λ1)是式(12)的最佳值。
证毕。
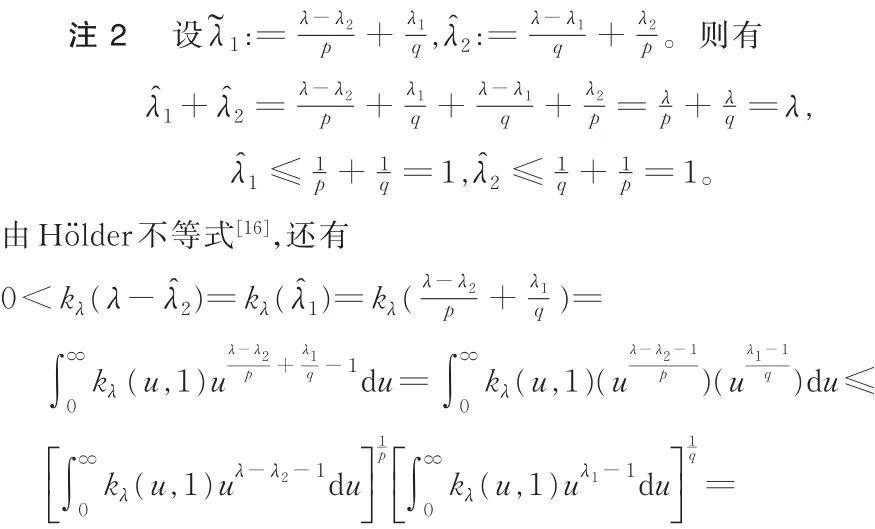

且式(11)右边变形为类似于式(12)的不等式:

证明若式(11)的常数因子为最佳值,则由式(14)及式(12),其唯一的最佳常数因子必可表示为,即有

若陈述(iv)成立,即λ1+λ2=λ,则式(11)导出具有最佳常数因子 kλ(λ1)的式(12)。


(iii)当 p=q=2时,式(15)与式(16)同时变为


