高原地区城市不透水面与地表温度时空分布研究

伍健恒, 孙彩歌, 樊风雷,2*

(1. 华南师范大学地理科学学院， 广州 510631； 2. 西藏大学高原地表遥感监测联合实验室， 拉萨 850000)

不透水表面主要指屋顶、沥青道路和广场等具有不透水性的地表面[1]，是城市的重要组成之一，体现城市化的程度，也是表征城市生态环境质量的重要指标[2]. 目前，城市不透水面数据主要通过遥感影像获得，主要方法包括指数法、光谱混合分析法、直接分类法、决策树模型以及回归模型等[3-4]. 中等分辨率影像结合线性光谱解混的方法能有效提高不透水面提取精度. 在方法层面，线性光谱解混关键在于端元的选择，分为固定端元和多端元选择2种方式. 结合固定端元与V-I-S模型[5]，WU和MURRAY[6]指出不透水面是高反照率地表和低反照率地表的组合，把城市地表类型表达为高、低反照率不透水面地表以及植被、土壤等4类端元并进行光谱混合分解，得到不透水面盖度(Impervious Surface Coverage, ISC). 多端元的光谱混合分析考虑到各像元组分的差异，采用不同的端元组合来分解. FAN和DENG[7]利用光谱参数度量实际地物光谱和标准光谱的相似性，选择最有代表意义的端元进行光谱混合分解. 在应用层面，国内有较多的学者基于线性光谱解混对我国东部城市的不透水面空间格局演变展开研究. 如：利用遥感数据对上海不透水面分布进行估算[8]；结合遥感指数，利用线性光谱解混提取广州不透水面[9]；按等级划分不透水面，分析深圳市不透水表面的时空演变[10]. 总体而言，国内不透水面研究成果主要集中在中国东部沿海地区[11-12]，对于中西部重要城市的不透水面研究关注相对较少.

较多学者以城区与郊区的地表温度为切入点展开城市热岛问题的研究. 传统的气象站点只能获取小区域的点数据，在城市遥感研究中，地表温度主要通过MODIS、AVHRR、ASTER以及Landsat数据获得. 由于MODIS、AVHRR和ASTER数据具有多个热红外波段，学者们提出了相对应的劈窗算法[13-15]；针对Landsat TM/ETM+数据仅有单个热红外波段的特点，覃志豪等[16]提出了高精度的单窗算法；Landsat8拥有2个热红外波段(TIRS10和TIRS11)，但TIRS11波段定标参数存在较大误差，故美国地质调查局不提倡基于Landsat8数据使用劈窗算法[17]，鉴于此情况，学者们提出了与TIRS10波段相适应的大气校正法[18]和单窗算法[19].

近年来，地表特征与城市热环境的关系得到广泛关注. 如：YUAN和BAUER[20]对比NDVI和ISC，发现ISC作为热岛效应指标更具适用性；王美雅等[21]通过线性、对数、指数以及多项式模型，对归一化不透水面指数[22]与地表温度进行回归分析，发现指数函数关系具有最大的相关系数；徐涵秋[23]利用逐步回归的方法，分析地表温度、不透水面、水体以及植被之间的关系，结果表明不透水面与地表温度呈正相关关系，不透水面对地表温度的影响与水体和植被对地表温度影响之和相当. 较多研究关注夏季时的不透水面与地表温度的关系[24-25]，较少关注冬季时的不透水面与地表温度的关系. 本文利用Landsat5和Landsat8影像获取不透水面和地表温度数据，分析不透水面与地表温度之间的空间分布特征和空间差异特征，以探讨不透水面与地表温度的变化规律，并对比不透水面对地表温度影响的季节性差异.

1 实验区与数据

1.1 实验区

拉萨市属于高原温带半干旱季风气候，多日照，年平均气温为7.4 ℃. 本文的实验区以拉萨市建成区为中心延展，东至拉林公路与318国道交界，西至昌东，南至拉萨火车南站，北至桑邓，其经纬度范围为90°53′ E～91°17′ E，29°35′ N～29°43′ N(图1). 实验区包含主城区以及周边郊区，其中，主城区包括中心片区、北城片区和东城片区，人类活动频繁，不透水面分布集中;周边郊区乡村聚落零散分布,不透水面密度较小. 实验区内不透水面分布差异突出，有利于探究不透水面对地表温度的影响.

1.2 研究数据

基于数据可获得性的考虑，本文选取实验区内云量相对较少的Landsat卫星影像进行信息提取，数据包括2009年1月18日、2009年8月30日两景Landsat 5影像以及2014年2月1日、2014年9月29日、2018年2月12日、2018年6月20日四景Landsat 8影像. 获取30 m空间分辨率数字高程数据GDEMV2作为信息提取的辅助数据. 同时，为比较Landsat数据所反演的地表温度，本文获取了上述6个成像时间对应的地表温度数据MOD11A1.

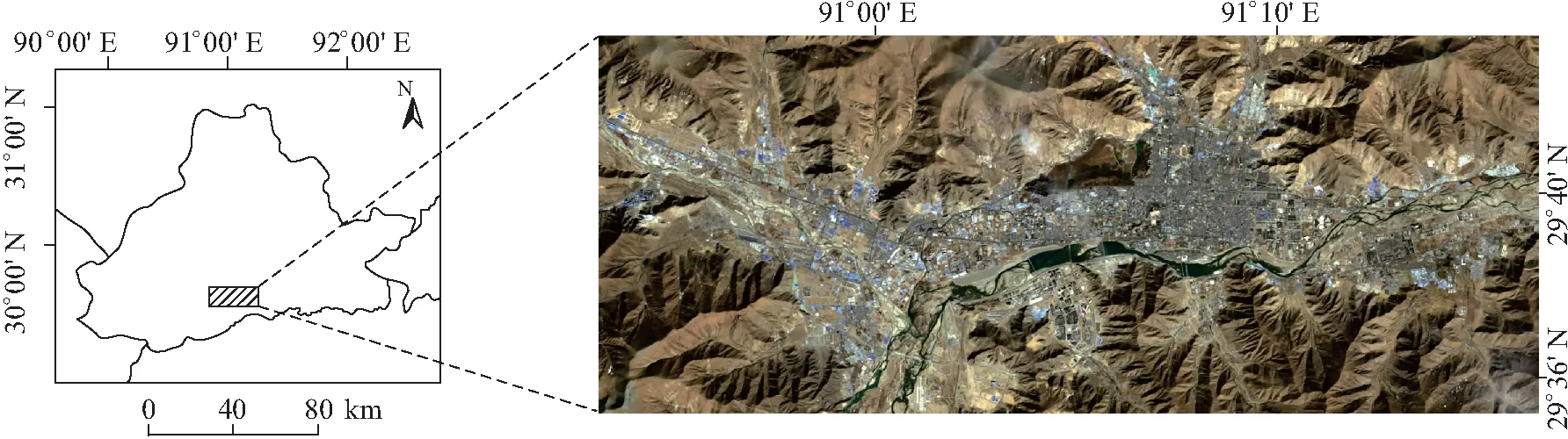
图1 拉萨市实验区

Figure 1 The experimental area of Lhasa city

2 研究方法

2.1 不透水面信息提取

基于线性光谱解混提取不透水面，主要过程包括数据降维、端元选择、混合像元分解和精度验证[26]. 遥感数据掩膜水体后，经过最小噪音分离变换保留前3个波段，选取高反照率不透水面、低反照率不透水面、植被和土壤作为端元，通过线性光谱混合模型估算各端元分量,将高、低反照率不透水面分量相加得到ISC.

线性光谱混合模型的假设是：像元在某一光谱波段内的反射率是各端元的反射率以及端元所占像元面积的比例作为权重系数的线性组合[27]. 考虑到端元丰度的物理意义，采用具有约束的线性光谱混合模型：

(1)

(2)

其中，Ri是第i波段的反射率；fk是端元k的丰度；Rik是端元k在第i个波段上的反射率；εi是第i波段的残差；i=1,…,m,m为光谱波段的数量；k=1,…,n,n为确定的端元数量.

2.2 地表温度反演

考虑到参数的可获得性，本文采用大气校正法反演地表温度. 大气校正法的主要原理是利用大气数据估算并剔除大气对地表热辐射的影响，获得地表热辐射强度并转化为对应的地表温度. 在地—气辐射传输中，与地表温度对应的黑体辐射亮度LT可以表达为

LT=[L-L↑-(1-ε)L↓]/(ε)，

(3)

其中，ε是实验区的地表比辐射率,可基于地表覆盖类型的加权混合模型估算得到[28];L是热红外辐射亮度值；L↑、L↓分别是大气向上、向下辐射亮度，是热红外波段在大气中的透过率，均在NASA网站上依据影像的地理位置以及成像时间计算获得(表1).

由普朗克公式的反函数推导出地表温度的计算公式：

T=K2/ln(K1/LT+1),

(4)

其中，K1和K2是定标参数，可通过查询影像数据的头文件得到.

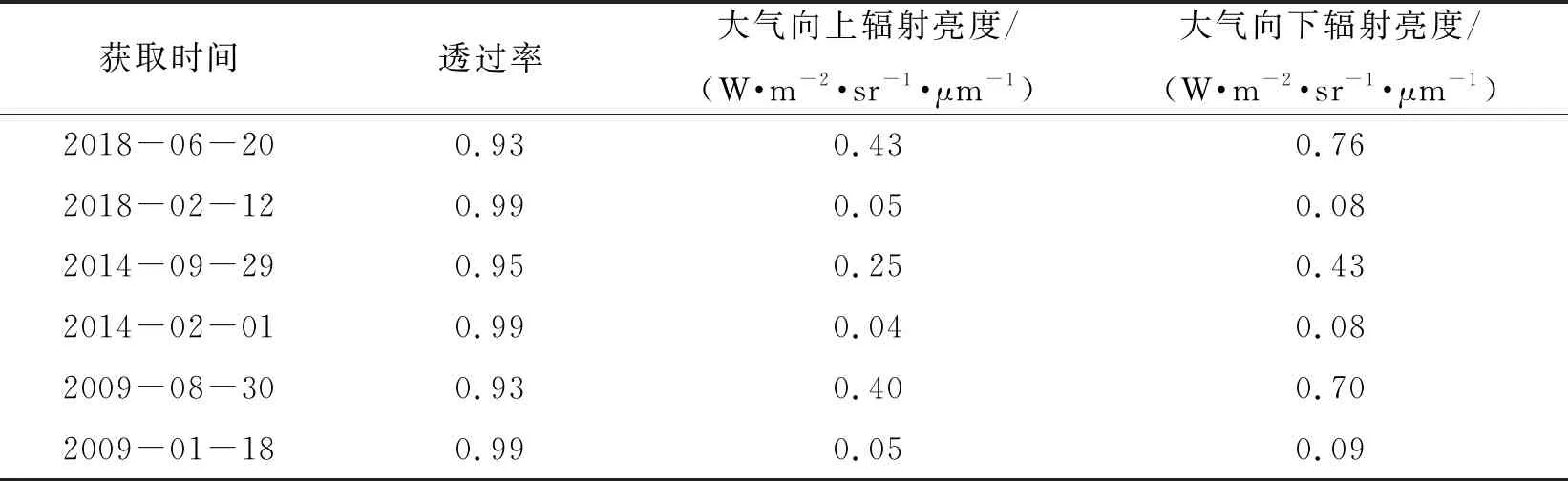
表1 大气参数信息Table 1 The information of atmospheric parameters

由于数据存在获取时间的差异，为使不同时相的地表温度具有可比性，对地表温度进行归一化处理，其计算公式为：

其中，T归一为归一化后的地表温度，表示像元间地表温度的相对高低，其值在0～1之间；T为像元的实际地表温度值，Tmin和Tmax是实验区内反演的最低地表温度和最高地表温度.

2.3 温度贡献指数

ZHANG等[29]以0.1为间隔，将ISC划分为10个等级，使用温度贡献指数量化不同等级的不透水面区域对城市热环境的影响：

(6)

其中，CIi是不同等级的不透水面区域所对应的温度贡献指数；Tdif是对应等级的不透水面区域的地表温度均值与实验区内地表温度均值之差；Si是该等级的不透水面区域所占的面积；Ssum是实验区总面积. 若CI为正数，则表示该等级的不透水面区域对城市热环境的贡献为正；若CI为负数，则表示该等级的不透水面区域对城市热环境的贡献为负.

3 结果与分析

3.1 ISC反演结果

由于实验区内冬季的植被信息并不明显，山区地形起伏大而导致阴影的存在，而阴影是混合像元的重要组成部分[30]，因此，基于3个时相的冬季Landsat数据，选择阴影、山体、高反照率不透水面和低反照率不透水面作为混合像元分解的端元. 利用GDEMV2高程数据掩膜海拔高于3 800 m的区域，同时对Band 7波段反射率大于0.2的区域进行掩膜，以抑制云层和土壤信息. 通过线性光谱解混的方法获得不透水面数据，统计得到2009、2014、2018年的ISC均值分别为0.08、0.09和0.13. 参考已有的ISC分级标准[31]，将不透水面划分为5级：高密度不透水面(ISC≥0.8)、中高密度不透水面(0.6≤ISC<0.8)、中密度不透水面(0.4≤ISC<0.6)、中低密度不透水面(0.2≤ISC<0.4)以及低密度不透水面(ISC<0.2)，详见图2.

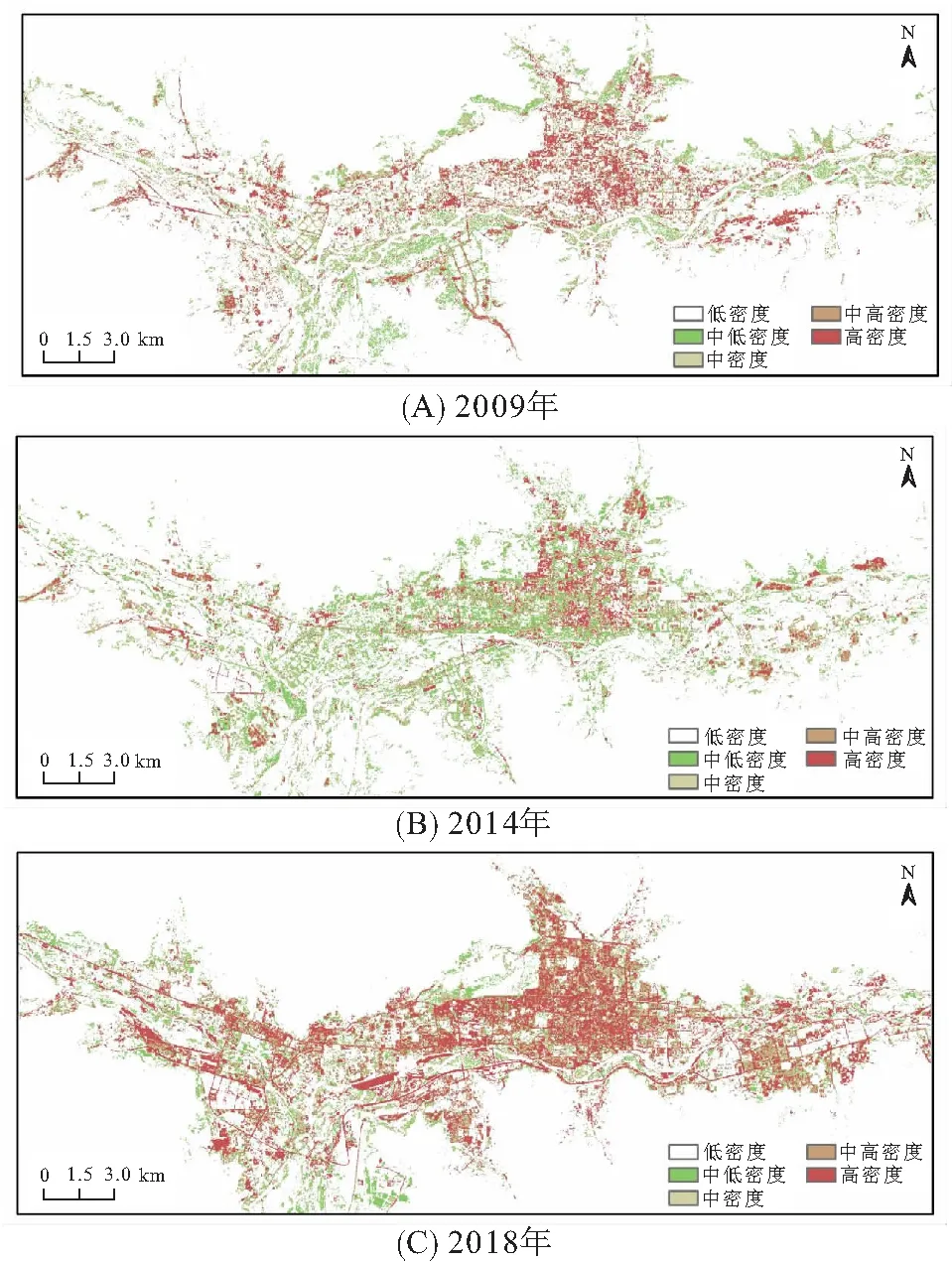
图2 不透水面的密度分布

Figure 2 The distribution of different densities of impervious surface

采用高分辨率Google Earth影像对ISC反演结果进行精度验证. 随机抽取实验区内200个样点，并对样点进行目视解译，得到ISC的实际值. 通过计算模拟值与实际值的相关系数对不透水面的提取精度进行评价. 由评价结果(图3)可知：3个时相的相关系数均大于0.75(通过0.01 的显著性水平检验).

3.2 地表温度反演结果

本文基于Landsat数据，结合大气校正法反演了拉萨市实验区2009—2018年冬夏两季的地表温度，并进行归一化处理，结果见图4. 由于地表温度数据MOD11A1能够适用于青藏高原不均匀的下垫面[32]，可以有效地解决高原气象站点稀少的问题，补充气象数据的不足[33-35]，因此，本文在缺乏实测数据的情况下，采用MOD11A1数据进行相对验证. 由验证结果(表2)可知：基于Landsat数据得到的T归一均值与归一化后的MOD11A1数据的均值相差0～0.07，表现出相似的城市热环境特征.

3.3 不透水面与地表温度的关系

本文以0.1为间隔，将ISC由低到高划分为10个等级，统计获得各等级ISC区域对城市热环境的温度贡献指数CI(由于CI过小，故将实际的CI乘以100).

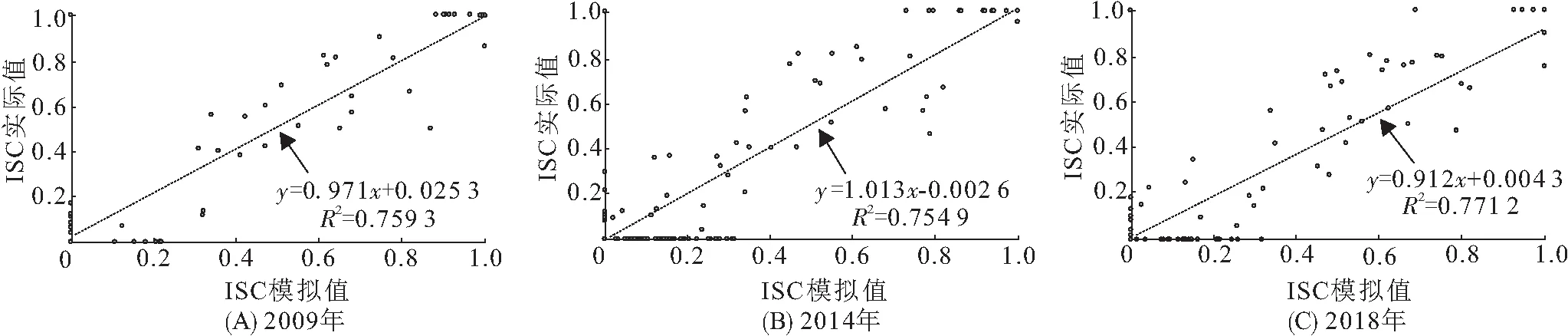
图3 ISC实际值与模拟值的拟合

图4 归一化地表温度分布

表2 Landsat反演结果与MOD11A1对比Table 2 The comparison between Landsat retrieval results and MOD11A1

由CI的统计结果(表3)可知：(1)冬季，当ISC<0.1时，CI为正数，ISC<0.1的区域对城市热环境的贡献为正；当ISC≥0.1时，CI基本为负数，ISC≥0.1的区域对城市热环境的贡献为负. 夏季，当ISC<0.1时，CI为负数，ISC<0.1的区域对城市热环境的贡献为负；当ISC≥0.1时，CI为正数，ISC≥0.1的区域对城市热环境的贡献为正. 这说明由于季节因素的影响，城市热环境对不透水面的响应存在2种不同的模式. (2)冬季，CI与ISC呈负相关关系. 夏季，当ISC<0.5时，CI呈现下降趋势，这可能是对于ISC<0.5的区域，植被和土壤是其主要的地表覆盖类型，减弱了不透水面对地表的增温作用；当ISC≥0.5时，CI呈现上升趋势，这可能是对于ISC>0.5的区域，不透水面成为其主要的地表覆盖类型，地表热量大部分以显热的方式表现，提高了该区域的地表温度.

本文为了细化不透水面对城市热环境的影响，以0.01为间隔划分ISC区间，统计每一个区间内所对应的T归一均值，对ISC与T归一进行一元线性回归分析. 由结果(图5)可知一元线性回归结果存在较大季节差异：(1)冬季，ISC与T归一的回归系数为0.625 4～0.817 3(通过0.01的显著性水平检验)，拟合程度较好.T归一随着ISC的增加而缓慢下降，ISC每增加0.1，T归一下降约0.01. (2)夏季，ISC与T归一的回归系数为0.036 3～0.115 8，拟合程度较差，简单的线性模型无法准确描述两者的关系. 夏季3个时相的ISC对T归一的影响表现为“V”形状：2009、2018年，当ISC<0.40时，随着ISC的增加，T归一下降；当ISC≥0.40时，T归一呈现上升趋势. 2014年，当ISC<0.23时，ISC与T归一呈现一定程度的负相关；当ISC≥0.23时，T归一随着ISC的增加而上升.

表3 各级不透水面盖度对热环境的贡献Table 3 The contribution of different ISC categories to the urban thermal environment

注:表中CI是将实际的CI乘以100.

图5 ISC与归一化地表温度的关系

3.4 不透水面扩展对热环境演变的影响分析

把当年ISC结果减去上一年的结果，差值小于-0.2则记为ISC下降，差值大于0.2则记为ISC上升，差值为-0.2～0.2则记为ISC基本不变，从而得到2009—2014年和2014—2018年的不透水面变化趋势(图6).

图6 ISC变化趋势

Figure 6 The change of impervious surface coverage from 2009 to 2018

结合ISC的均值计算结果和表2，并比较分析图2A、B及图6A，可知：2009—2014年，ISC均值由0.08增加至0.09，夏季的T归一均值由0.76下降至0.58,冬季的T归一均值由0.50上升至0.54. ISC上升的区域主要分布在郊外的各个文化、旅游和工业产业园区，市政设施建设集中在东城新区、东嘎新区以及柳梧新区；ISC下降的区域主要分布在各住宅园区以及拉鲁湿地，零散分布于老城区. 夏季的T归一均值下降了0.18的原因可能是：该时期城市内部结构得到调整，产业园区向高新区转移，同时城市中加强了绿化建设. 城市绿化水平的提高导致高密度不透水面向中低密度不透水面转变，城市绿地切割了原有的城市建设用地，打破了由于硬化地表所造成的连片高温，改善了城市热环境. 冬季的T归一均值上升了0.04的原因可能是：冬季植被减少，裸土和不透水面替代了植被，增强了地表的保温能力.

结合ISC的均值计算结果和表2，并比较分析图2B、C及图6B，可知：2014—2018年，ISC均值由0.09增加至0.13，夏季的T归一均值由0.58上升至0.61,冬季的T归一均值由0.54降低为0.53. ISC上升的区域集中在拉萨河沿岸的郊区，不透水面的扩散方向具有“东延、西扩、南跨”的特征. 夏季的T归一均值上升了0.03的原因可能是:郊区的大量开发导致低密度、中低密度不透水面分别向中高密度、高密度不透水面转变，不透水面的扩散减弱了蒸腾蒸发作用，同时不透水面向城区内部填充，连片的不透水面造成聚合效应，热量交换以显热交换为主，提高了实验区内的地表温度. 冬季的T归一均值的下降幅度为0.01，说明地表温度的变化波动较小，基本维持了地表温度的稳定，可能是因为冬季的地表温度对一定盖度以上的不透水面不敏感，导致形成了稳定的城市热环境.

4 小结与展望

本文运用Landsat影像，得到2009—2018年拉萨市实验区内不透水面与地表温度数据，讨论了高原地区城市不透水面对地表温度的影响，其主要结论如下：

(1)由于季节因素的影响，城市热环境对不透水面的响应存在2种不同的模式.

(2)冬季，CI随着ISC的增大而减小，CI与ISC呈负相关关系. 夏季，当ISC<0.5时，CI呈现下降趋势；当ISC≥0.5时，CI呈现上升趋势.

(3)冬季，ISC与地表温度存在较强的线性关系：随着ISC增加，地表温度缓慢下降. 夏季，ISC与地表温度不是简单的线性关系：ISC对地表温度的影响表现为“V”形状.

本文揭示了不透水面与地表温度关系的季节性差异，为城市规划和城市生态环境保护提供一定参考，但存在以下几个需要改进的方面：第一，需要进一步结合特征空间变换模型扩大不透水面与土壤的特征差异，提高不透水面提取的精度. 第二，由于缺少实测数据，采用1 km分辨率的MOD11A1数据对30 m分辨率的Landsat地表温度数据进行相对验证具有不确定性，难以准确反映反演精度，在理想的情况下应在实地布置多个实测点，为客观评价反演结果提供数据支撑. 第三，冬季，随着ISC的增加，地表温度降低，这可能与拉萨独特的地理位置、建筑材料和季节因素有关，其机理仍然需要深入研究. 第四，本文构建不透水面与地表温度的关系采用简单的一元线性回归模型，但地表温度本身存在空间的自相关性，考虑地表温度的空间自相关，结合空间滞后模型，更为准确描述不透水面与地表温度的关系将是往后研究重点.