基于深度神经网络的高频谱效率频分复用系统的信道估计方法

陈嘉润， 余宝贤， 王剑莹， 张 涵

(广东省心脑血管个体化医疗大数据工程技术研究中心∥华南师范大学物理与电信工程学院， 广州 510006)

随着无线技术的发展,移动通信不断取得飞跃式的进步,同时频谱资源显得愈发珍贵,因此高频谱效率频分复用(Spectrally Efficient Frequency Division Multiplexing，SEFDM)系统应运而生[1-4]. SEFDM作为一种非正交传输技术,通过压缩正交频分复用(OF-DM)信号子载波之间的间隔,可使在相同的频谱带宽内能传输更多的信息,从而获得更高的频谱效率. 然而,压缩子载波破坏了子载波间的正交性,引入了载波间干扰(Inter-Carrier Interference,ICI).

针对SEFDM引入ICI的问题,我们提出补零的SE-FDM结构以及与OFDM系统简单有效的单抽头迫零频域均衡算法[5],然而它是以已知信道状态信息(Chan-Nel State Information,CSI)为前提的. 虽然有研究[6-7]分别提出时域上基于块状导频的全信道估计和部分信道估计(Partial Channel Estimation,PCE)，但目前仍缺乏有效的信道估计方法作为支撑. 浙江大学赵民建团队[8]通过采用具有连续相位循环前缀(Cyclic Prefix,CP)的梳状导频改进PCE,提高了估计精度. GHANNAM等[9]则提出频域信道估计方法,将子载波按正交性分组,通过分组设计块状导频,以更多的系统开销为代价,实现了对每个子载波信道的精确估计.

在这些研究的信道估计中，都要求在SEFDM中相互正交的特定载波上放置导频符号. 然而当所取压缩因子的分母较大时,SEFDM中正交子载波集合的元素个数通常小于信道抽头数,此时若采用最小二乘法(Least Square,LS)等线性估计方法,将产生错误平台[10],严重影响了系统的性能.

随着计算机计算能力的提高及大数据的发展,深度学习被广泛应用于通信系统中. 文献[11]将其应用于基于CSI的室内定位中;文献[12]将深度神经网络(DNN)应用于信道均衡中;文献[13]将DNN应用于信道解码中;最近,DNN网络被应用于4G下行链路(OFDM)系统端到端的信道估计与符号检测[14],显示出深度学习在无线通信系统端到端处理的性能优势. 然而,上述方案受限于ICI,无法将其直接应用于SEFDM系统.

针对传统SEFDM信道估计方法对压缩因子的局限性,本文创新性地开展了基于DNN的SEFDM系统信道估计研究. 结合PCE的导频放置方式,将导频符号的接收信号作为DNN的输入信号,对信道时域进行预测. 具体来讲,通过一个4层的全连接DNN结构提取信道特征,完成了时域信道估计.

1 仿真方法

1.1 SEFDM系统模型

SEFDM是一种非正交的多载波通信技术,起源于1975年MAZO博士提出的超奈奎斯特(Faster Than Nyquist,FTN)概念[14]. 其基本思想是相对于OFDM进一步压缩子载波之间的间隔,从而达到节省带宽的目的. 与此同时也破坏了OFDM中子载波间的正交性,引入了ICI.

由于对子载波的压缩,SEFDM的发送信号无法直接由离散傅里叶逆变换(Inverse Discrete Fourier Transform,IDFT)产生,本文沿用补零截断法来产生SEFDM的发送信号. 如图1所示,SEFDM信号可以由N点的IDFT产生[15],即符号pk,k=0,1,…,Q-1.末尾插入Q1=N-Q个0,对N个数据一起进行I-DFT处理,并将结果中末尾的Q1个数据舍去,即可得到 SEFDM的时域信号.

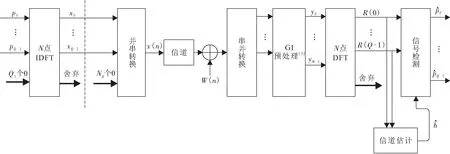
图1 SEFDM系统的框架

在串并转换之前，插入Ng个0作为保护间隔,其中Ng不小于信道抽头数，以保证SEFDM免受符号块间的干扰,同时定义NZP=Q+Ng.α=Q/N称为SEFDM的压缩因子,对SEFDM而言,总有α<1. 当α=1时,SEFDM将退化为OFDM. 因此,SEFDM相对于OFDM的频谱效率提高了(1-α)/α×100%. 与发送端对应,接收端同样使用N点离散傅里叶变换(Discrete Fourier Transform,DFT)恢复SEFDM的频域信号. 此时SEFDM接收信号可以表示为

R=HΦP+W，

(1)

其中,H是代表信道频域冲激响应的N×N维对角矩阵,P代表传输的Q×1符号块,W代表独立同分布且均值为0的复高斯随机噪声.Φ为一个具有循环移位特征的埃尔米特矩阵,第(k,i)个元素为:

(2)

由式(1)可知，接收信号不仅包括当前符号,还包含其余符号的联合干扰. 特别是当α=1时,Φ是一个单位矩阵,此时SEFDM将等效于OFDM.

已有定理证明[7]:当SEFDM的压缩因子为有理数时,每相邻一定间隔的子载波将相互正交. 具体而言,假设α=b/c,其中b、c均为正整数且最大公约数为1,则SEFDM中所有相距为c的子载波间相互正交. PCE是在这些相互正交的子载波上放置导频,在其余位置上置零[9]，此时所有导频之间相互正交,矩阵Φ退化为单位矩阵. PCE方法放置导频的频点可以表示为(k0,…,kM-1),其中km=m×c,m=0,…,M-1，且m=Q/c. 频域的LS信道估计方法[13]可以表示为

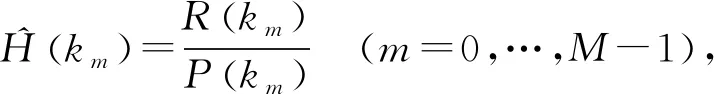
(3)

其中,km代表放置了导频的频点. 估计出频点上的CSI后,再通过插值方法得到完整的CSI.

1.2 DNN系统模型

本文采用DNN模型[10,16]，其基本结构如图2所示.

图2 DNN的结构

DNN的每一层神经元数目不定,层与层间发生级联，第l层与第l+1层之间的关系可表示为:

Yl+1=f(θl,l+1Yl+bl),

(4)

其中,Yl+1表示第l+1层的输出向量;θl,l+1表示第l层与第l+1层之间的权重矩阵;bl表示第l层的偏置向量;f则表示该层选用的非线性激活函数.

在采用的DNN中,模型的输入信号是采用PCE方法放置导频符号时的接收信号. 由于DNN处理的是实数,因此需将每个子载波上的接收信号拆分为实部和虚部,再作为DNN的输入信号. 同理,信道时域也拆分为实部和虚部,再将其作为DNN的输出信号. 采用的子载波数Q=24,信道抽头数T=6,所以DNN的输入层和输出层的神经元数目分别为48个和12个. 综合考虑DNN性能与复杂度,采用4层DNN,每层神经元的个数分别是48、300、150和12;第2层和第3层为隐藏层,皆采用ReLU函数作为激活函数;输出层则采用Sigmoid函数作为激活函数,以限制其输出范围.

1.3 仿真设置

在本仿真中,DNN参数采用He初始化[17],训练参数过程使用Adam优化方法[10]. DNN的训练目标是将输出信号和标签之间的误差最小化,采用L2损失函数[10]:

(5)

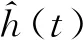
2 结果与分析

验证本文方案所使用的仿真软件为Python及Matlab. 前者用于DNN模型的训练及调试，后者用于训练数据和测试数据的产生，以及在恢复出CSI后执行信号检测. 在仿真中,统一采用具有24个子载波的SEFDM系统,调制方式为4QAM,仿真所用信道为COST207远郊地区(Rural Area)[5]信道模型.

2.1 不同压缩因子对性能的影响

首先验证不同压缩因子下所提方法的性能. 按PCE放置导频的方式,即在一组相互正交的所有子载波上放置导频符号,对比基于DNN的信道估计和LS的MSE性能. 在本仿真中,α分别为2/3、3/4、5/6,对应的导频符号数目分别为8、6、4. 如图3所示,在相同的压缩因子下,基于DNN信道估计方法的MSE均比LS的小. 特别是在导频数量小于信道抽头数(α=5/6)时,尽管二者的MSE均有所提升,但后者遭受误码平台的影响,前者保持了与LS在OFDM系统中相近的MSE. 在导频数量不小于信道抽头数时,本文所提方法在不同压缩因子下的MSE基本相同,且与OFDM的性能几乎一致,由此说明了该方法对压缩因子系数变化具有极强的鲁棒性.

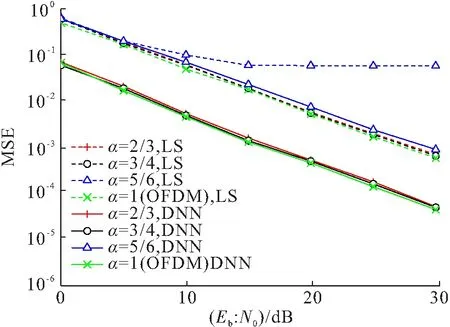
图3 不同压缩因子α取值的MSE曲线

在上述信道估计的基础上,使用估计得到的CSI对数据信号进行信道均衡处理,并通过球面译码[13](Sphere Decoding,SD)进行解调,其BER性能如图4所示. 当CSI已知时,随着压缩因子的增大,压缩因子载波所引入的ICI减小,译码性能更好; 而当压缩因子相等时,使用基于DNN的信道估计方法得到的CSI进行均衡和解调时，DNN方法的性能优于LS方法，且在导频数小于信道抽头数(α=5/6)时尤为明显. 上述结果符合预期且与图3的结果一致,即本文所提方法相对于LS的性能提升归因于信道估计性能的改善,反映了本文方法的有效性.

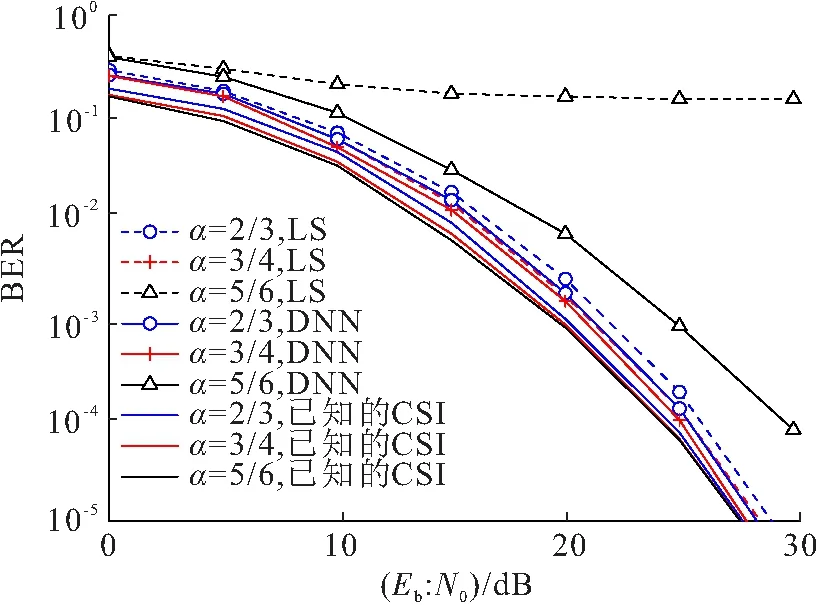
图4 不同压缩因子α取值时的BER曲线

2.2 不同导频数对性能的影响

保持α=3/4不变,并在相互正交的位置放置不同数量的导频符号,对比研究基于DNN的信道估计方法与LS的MSE. 在放置的导频数量相同时,DNN信道估计方法的MSE均小于LS方法(图5),其中,当放置的导频数量小于信道抽头数时,LS遭受了错误平台的影响,然而DNN保持了与LS在导频数为6时相近的MSE. 本文所提方法在放置不同导频数时具有较为稳定的估计性能,由此说明了该方法对导频数具有较强的鲁棒性.

图5 不同导频数变化时的MSE曲线

与图5对应,使用上述估计得到的CSI对数据信号进行信道均衡,并通过SD解调,得到BER曲线(图6). 当导频数量相同时,使用基于DNN的信道估计方法得到CSI,并对CSI进行均衡和解调，其性能优于LS方法. 在导频数小于信道抽头数时,这一现象尤为明显. 该结果符合预期，且与图5的结论一致,即本文所提方法具有更加优越的信道估计性能,系统性能得到提升说明了该方法的有效性.

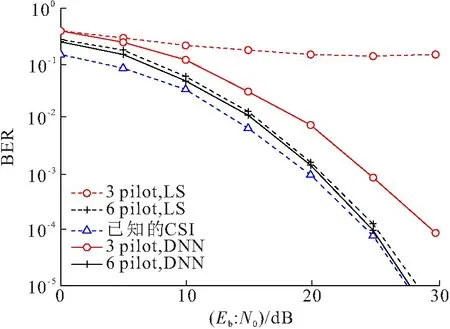
图6 不同导频数变化时的BER曲线

3 总结

研究了DNN在SEFDM信道估计中的应用性能,根据压缩因子设计等间隔且相互正交的导频结构，并以最小化MSE作为目标函数，使用4层全连接DNN进行信道估计. 结果表明：相对于传统的LS方法，基于DNN的SEFDM信道估计方法实现了更优的MSE和BER性能，同时提高了对压缩因子和导频数量的鲁棒性，因此该方法具备更强的有效性和实用性.