基于ScikitLearn的SVM分类器算法优化

左一鹏, 陈 辉

(上海电力大学 自动化工程学院, 上海 200090)

机器学习中的数据分类问题在机器人导航、无人驾驶、垃圾邮件过滤、手写数字的识别等领域中扮演着不可或缺的角色[1]。常见的数据分类算法有K近邻[2]、朴素贝叶斯[3]、决策树[4]、Logistic回归[5]和支持向量机(Support Vector Machines,SVM)[6]。目前应用最为广泛的是SVM分类器,其核心思想是线性分类器,最初解决线性可分问题,然后拓展到非线性映射,将低维空间内不可分的样本映射成高维空间线性可分的样本,通过超平面将样本分割成不同类别。SVM分类器的优势在高维空间内非常有效,即使在数据维度比样本数量大的情况下仍然可高效利用内存。SVM的核函数的通用性较强,可根据数据集的特点选择核函数类型以及参数。SVM分类器存在的问题是对小量数据分类时易出现过拟合现象,泛化性不强。带有核函数的SVM一般依靠经验选择参数,且仅能达到局部最优,手动调参方式的效率低下,实际应用困难。针对SVM参数调整问题,目前学者们已提出很多种优化算法,如人工蜂群算法结合SVM[7],基于蝙蝠算法优化的方法结合SVM[8]和结合KNN算法的改进[9]等。但是针对SVM使用过程中的参数选择,没有一个固定的方法。

本文从提高实际使用时效率的角度出发,针对SVM参数调整及优化问题,提出一种基于Scikit-Learn的SVM参数调整优化方法。结合网格搜索以及交叉验证的方法对最优参数范围进行搜索,利用Python机器学习库Scikit-Learn对不同参数、不同核函数的分类结果进行可视化观察,并在网格上显示其最优参数范围,寻找准确率高的参数分布,再通过迭代的方法提高对最优参数的求解,最终实现数据的准确分类。

1 SVM算法概述

1.1 数学原理

SVM分类器按监督学习方式对数据进行二元分类,通过分类超平面能使分类间隔最大化[10]。在分类问题中,令给定的输入数据样本集为:X={X1,X2,X3,…,Xm},学习目标为:y={-1,1},每个样本Xi(i=1,2,3,…)包含n个特征,即Xi=[x1,x2,x3,…,xn]。针对在二维平面上分布的两种数据类型,需要一个超平面对数据进行分割。超平面可以用线性方程表示为

ωTXi+b=0

(1)

式中:ω——法向量,决定超平面的方向;

b——偏移量,决定超平面与原点之间的距离。

对于线性分类问题,可以通过设定f(Xi)=ωTXi+b为决策函数进行处理。对于所有样本点,均满足如下条件:即y=1时,认为ωTXi+b≥1;如果y=-1时,则ωTXi+b≤-1。

根据点到面的距离公式,可知空间中任意一点样本Xi到超平面(ω,b)的距离为

(2)

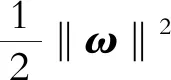
(3)

图1为以鸢尾花数据集为例的SVM二分类最大间隔分类示意图,横坐标为维吉尼亚鸢尾、山鸢尾花萼长度,纵坐标为花萼宽度。 SVM的二分类就是在两个类别不同特征的分布中找到一个使得两个类别区分间隔最大的分割线。

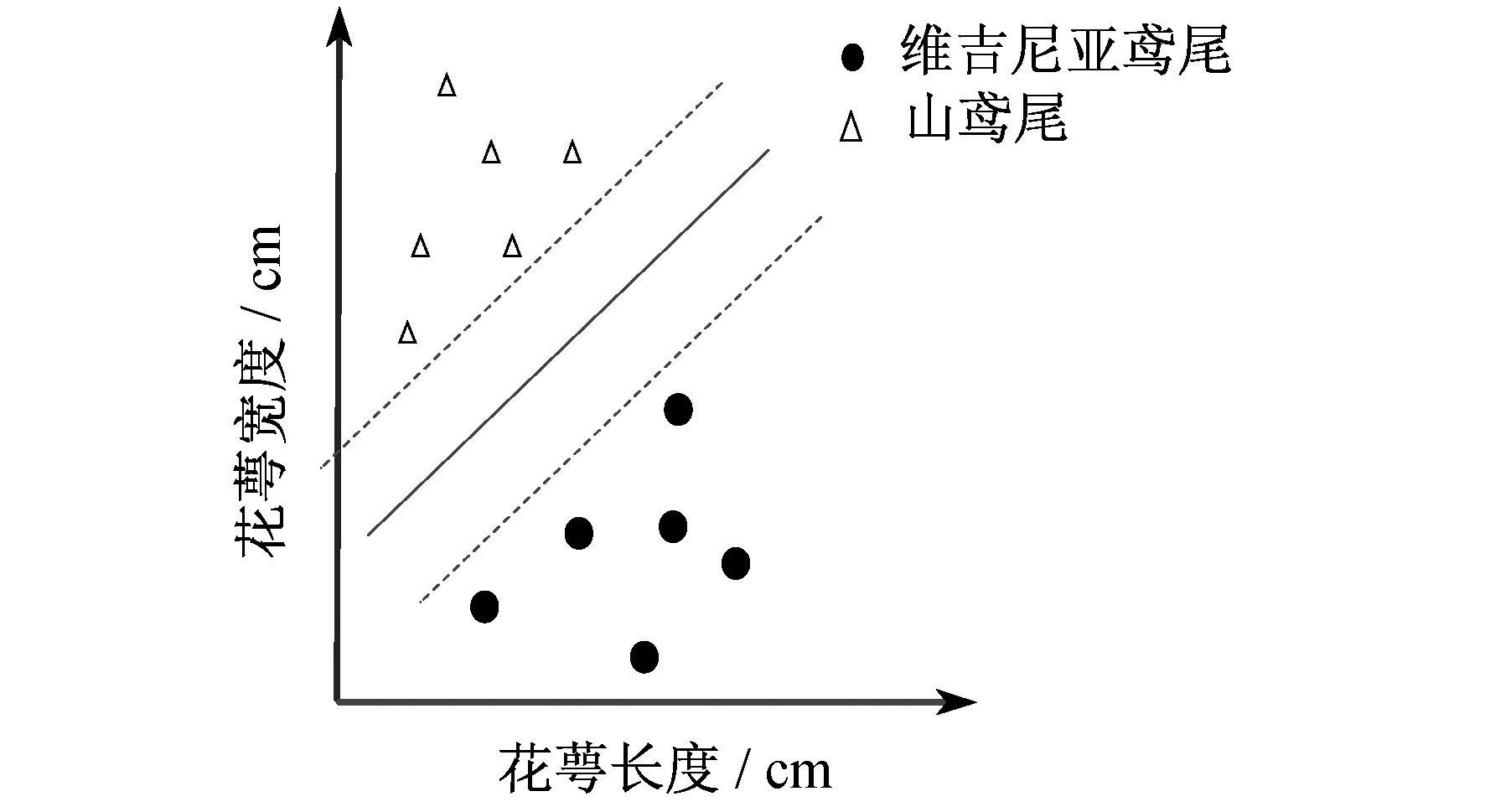
图1 SVM二分类最大间隔分类示意

1.2 核方法

通常线性不可分问题可能是非线性可分的,即在特征空间中存在超曲面将正类和负类分开。通过非线性函数将可分问题从原始特征空间映射至更高维希尔伯特空间,从而转化为线性可分问题。

设χ是输入空间,即Xi∈χ,χ是Rn的子集或离散集合,又设H为特征空间,如果存在一个χ到H的映射:

φ(x):χ→H

(4)

使得对所有x,z∈χ,函数K(x,z)满足条件

K(x,z)=〈φ(x),φ(z)〉

(5)

则称K为核函数[11],其中φ(x)为映射函数。核函数主要包括:多项式核、径向基函数核、拉普拉斯核和Sigmoid核等。

1.3 非线性SVM

针对数据集的多样化,SVM分类器可进行针对性分类,对于不能直接线性分类的数据集需要使用非线性SVM分类[12]。通过特征添加,将n维平面空间映射到n+1维空间,将二维空间平面映射到三维空间以便于类别的区分,从而将数据集变为可线性分离。

2 SVM分类器算法优化

2.1 核函数选择

在数据线性不可分的情况下,SVM首先在低维空间中完成计算,然后通过核函数将输入空间映射到高维特征空间,最终在高维特征空间中构造出最优分离超平面,将不易分离的非线性数据分类。高斯径向基核函数(Radial Basis Function,RBF)[13]是一种局部性强的核函数,可将一个样本映射到一个更高维的空间内。其应用广泛,通用性强,更适合在无先验知识情况下使用。本文选用RBF核作为核函数进行数据分类。其公式为

(6)

2.2 RBF核函数参数调整

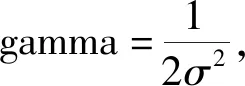
2.3 网格搜索法调整参数

网格搜索法[14]是通过在指定的数值范围内,按照一定次数将参数进行调整试验,以网格形式表示,得到相应的最优参数组合。但网格搜索法受限于数据量的大小以及选定产生网格数据的大小,数据大时难以得出结果。针对该问题,可利用多次提取网格搜索的参数最优值在相邻范围内继续进行网格搜索以及适当扩大网格搜索的数据量,使计算结果逐渐趋近于最优参数的值[15]。本文通过逐渐趋近的方式进行网格搜索调参,构建可以自动迭代的网格搜索法。

2.4 循环迭代网格搜索

基于手动调整网格搜索思想,通过设置自动循环进行网格调参。在每次网格搜索结束后,利用函数调用对搜索C和gamma的最优参数值进行读取,得到网格中的最优参数值,观察网格搜索结果分布,确定最优参数值。对于数值较小的gamma值,选择以10倍基准为上限,0.1倍基准为下限;对于参数较大的C以2倍基准为上限,0.01倍基准为下限,以此为下一次的迭代区域进行搜索。该方法首先根据网格参数的搜索得到最优值,再通过最优值设定上下限,并在区域内进行进一步搜索,持续迭代至准确率稳定。

3 实验结果与分析

为了验证所提方法的有效性,以鸢尾花数据集为测试对象(包含150个数据,分为3类,每类50个数据,每个数据包含4个属性),进行分类测试。实验在Ubuntu16.04操作系统、Scikit-Learn开发环境下进行,程序为Python3.7语言。可通过花萼长度、花萼宽度、花瓣长度、花瓣宽度4个属性预测鸢尾花卉属于维吉尼亚鸢尾、山鸢尾、杂色鸢尾3个种类中的哪一类。在本次实验测试中,选取花萼长度和花萼宽度两种特征进行分类。

3.1 不同核函数的分类

在鸢尾花数据集中,从花萼长度和花萼宽度两项数据的分布,观察3种花的不同。维吉尼亚鸢尾花萼长度分布在4.9～7.9 cm,杂色鸢尾花萼长度分布在4.9～7.0 cm,山鸢尾花萼长度分布在4.3～5.8 cm。维吉尼亚鸢尾花萼宽度分布在2.2～3.8 cm,杂色鸢尾花萼宽度分布在2.0～3.4 cm,山鸢尾花萼宽度分布在2.3～4.4 cm。从整体的分布上看,花萼长度由低到高排序依次为山鸢尾、杂色鸢尾、维吉尼亚鸢尾,花萼宽度由低到高的排序依次为杂色鸢尾、维吉尼亚鸢尾、山鸢尾。在这些数据中会有部分不同种类花的花萼长度、宽度分布在同一区间。机器学习分类过程中,会根据实际样本的数据分布情况以及参数的设定,确定一个能够较好的将两者分类的界限。实验中,选择了4种不同类型的核函数进行分类结果比较。分类结果如图2所示。

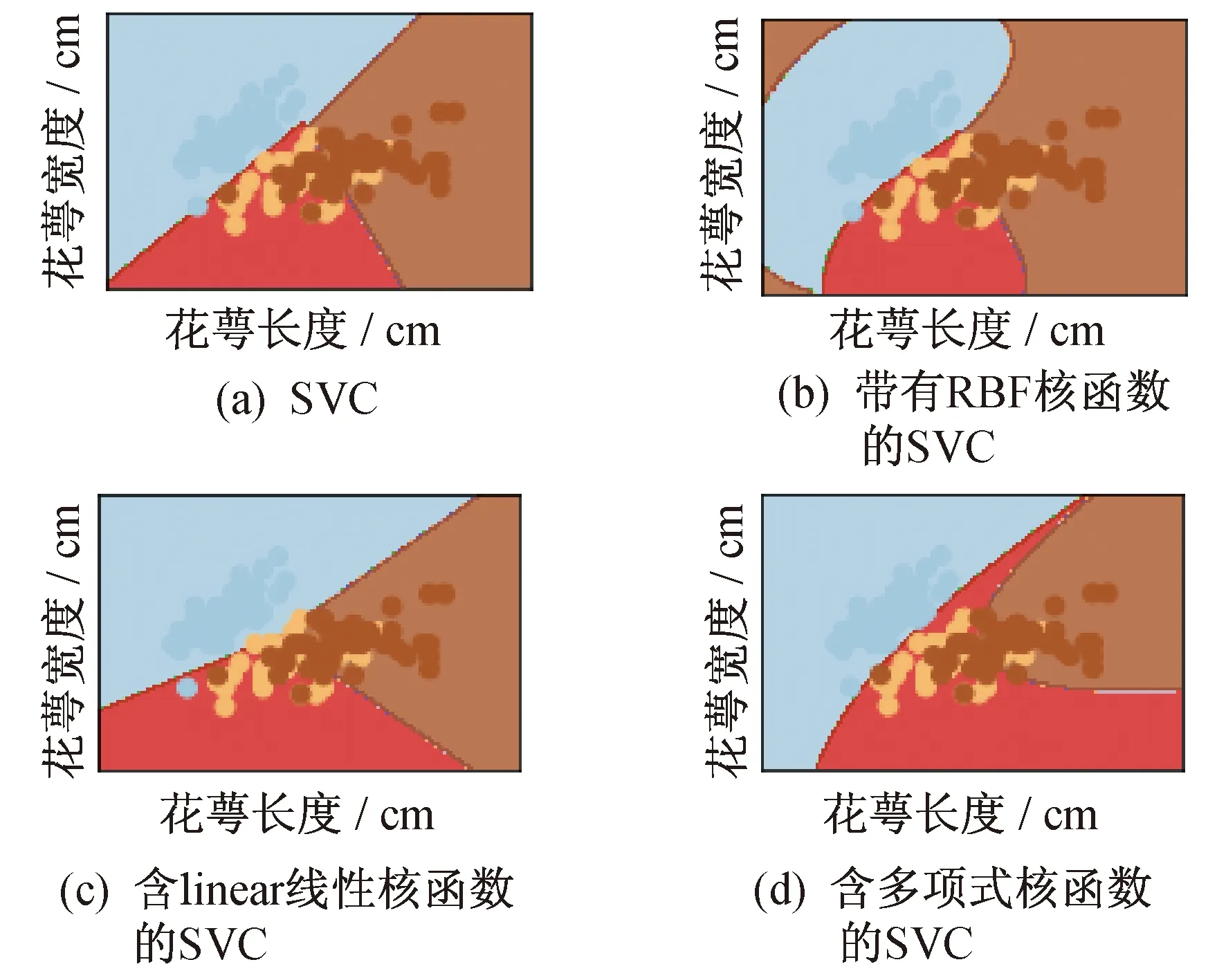
图2 不同核函数的分类结果

其中,SVC是SVM中的一类,用于样例数量少于10 000时的二元和多元分类。由图2可以看出:图2(a)、图2(c)、图2(d)的分类结果中,在两种类别的分割上不是很合理,其中图2(a)和图2(c)的分割近乎直线方式,分类结果对于实际数据集的效果不理想,主要是因为实际分类的对象是具有某种特征范围内的一类,而不是仅仅具有线性关系就可以分类;图2(b)和图2(d)的分类结果比较平滑,但是图2(d)的类别划分中,有的近似于直线,有的类别划分延伸较长。同时结合表1可以看出,带有RBF核函数的SVC分类准确率略高一些。

表1 不同核函数下SVM分类结果对比

3.2 改变RBF核函数参数

为了提高带有RBF核函数的SVM分类器的准确率,进一步调整参数。将gamma参数设置为5,并保持不变,仅对参数C进行调整,采用数量级调参的方式,即改变C参数的数量级,观察这种变化对分类准确率的影响,结果如表2和图3所示。

表2 改变参数C对分类准确率的影响

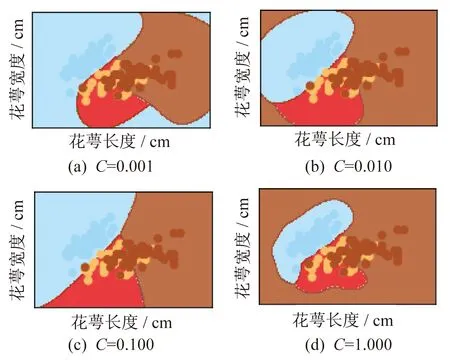
图3 RBF核函数不同参数值的分类结果

由表2可知,C的数值由0.01变为0.1后,分类准确率提升幅度较大,这是因为将C值调高后,提高了对总误差的惩罚系数,在程序运行中,会增加对准确率的权重,因此准确率大幅上升。由图3可知,改变C参数的数量级在分类结果的改进中并不是非常明显,仅图3(d)的分类结果区分比较明显,不过这种方式效率比较低。手动更改gamma和C的参数值对于分类的结果提高并不显著,因此需要一种可以高效的求解最优参数的方法。

3.3 网格搜索法

在初次进行网格搜索时,设置参数C的范围为10-2～1010,gamma的范围为10-9～103,都分成13等份。输出网格排列的准确率图像以及准确率最高一组的C与gamma的参数值。根据Scikit-Learn的使用特点,并为了便于可视化,选择杂色鸢尾和维吉尼亚鸢尾两种进行二分类。

图4表示经过网络搜索后,不同参数下的分类结果,其中花萼长度(单位cm)作为横轴,花萼宽度(单位cm)作为纵轴。蓝色数据点表示杂色鸢尾数据,蓝色区域表示分类后对判断属于这一花类范围的划分;红色数据点表示维吉尼亚鸢尾,红色区域表示分类后对属于这一花类范围的划分。

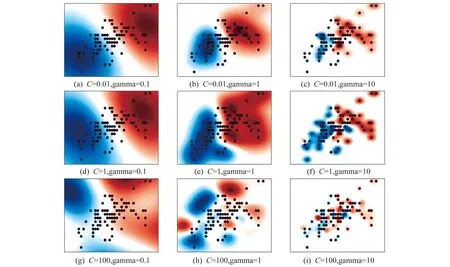
图4 初次网络搜索的分类结果

由图4可知,C=1,gamma= 0.1时,准确率达到97%,为手动调整参数的最高准确率,但是不能确定是否为全局最高,需要进一步进行优化,以确定全局最优,并且提高寻找效率。

参数C与gamma对应的准确率分布如图5所示。

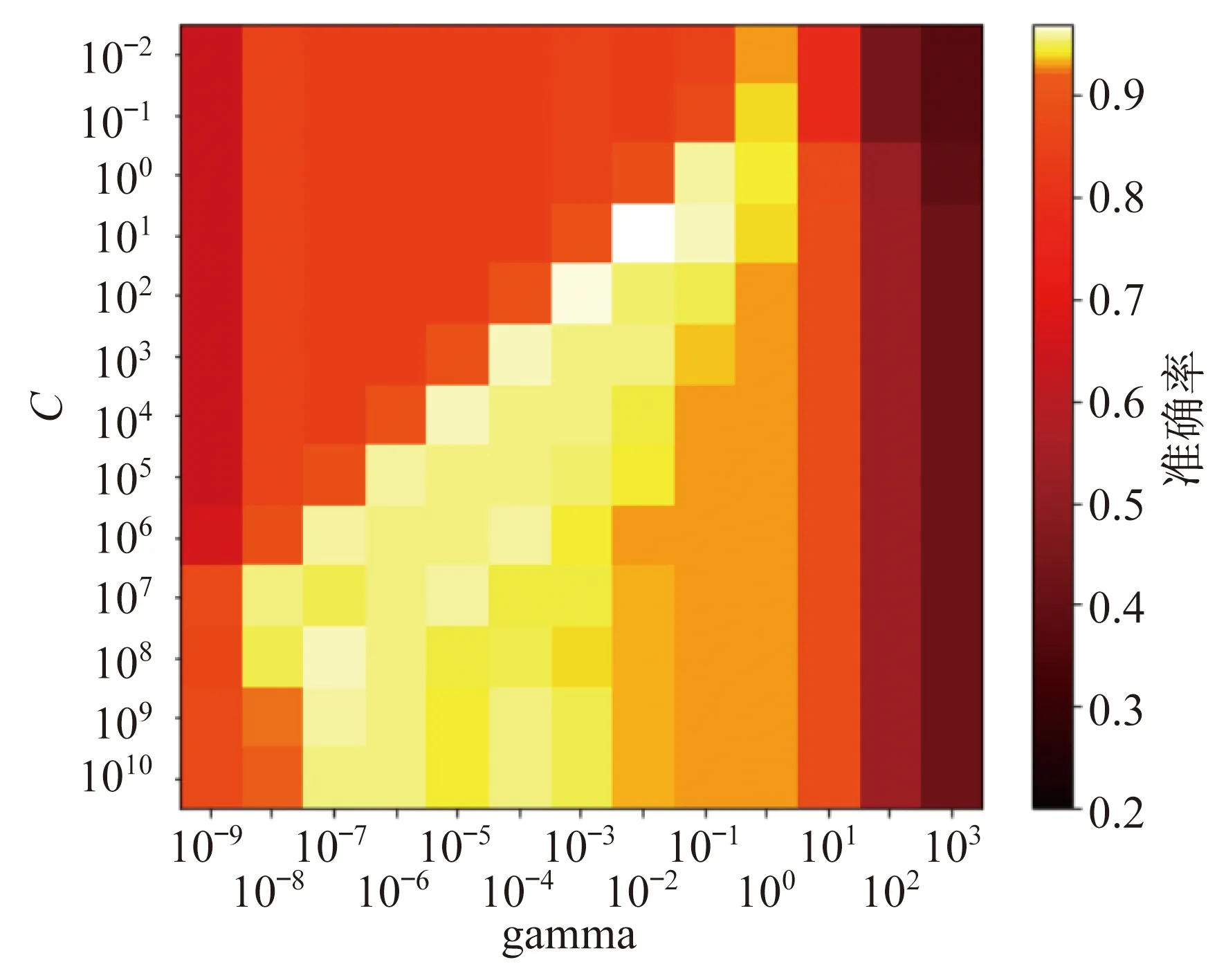
图5 参数C与gamma对应的准确率分布

由图5可知,当C为1时,观察不同的gamma数值从0.001～1变化,发现准确率仅在一定范围内增加或者降低,没有得到全局最优参数值。

采用网格搜索法调整参数,5次网格搜索结果如表3所示。

表3 5次网格搜索结果

由表3可以看到,在图5中的一个区域范围内,手动调整参数准确率比较高。由于第一次设置的数值间隔大且所分组数较少,得到的可产生最高准确率的一组参数只是与最优参数相近的数值。因此,采用逐渐逼近法进行网格搜索,逐渐缩小参数的搜索范围,同时适当增加所分数组数量。图6是针对表3的参数进行实验所得出的分类效果,花萼长度(单位cm)作为横轴,花萼宽度(单位cm)作为纵轴。蓝色数据点表示杂色鸢尾数据,蓝色区域表示分类后对判断属于这一花类范围的划分;红色数据点表示维吉尼亚鸢尾,红色区域表示分类后对属于这一花类范围的划分。

3.4 自动迭代网格搜索

网格搜索在一定范围内的最优参数求解效果明显,但受网格搜索大小限制,只能先求出部分参数,然后逐步手动输入下一个范围,增加了工作量,且效率较低。因此,本文根据分类结果图中所示意的最优参数分布,采用自动循环迭代的网格搜索进行参数的选择。图5中C=10,gamma=0.01时,对应的白色表示在该网格的搜索下准确率最高一组参数。参数gamma较小,选择以10倍基准为上限,0.1倍基准为下限,对于较大的参数C以2倍基准为上限,0.01倍基准作为下限得出gamma和C的最佳参数范围,通过进行迭代以进一步求得更精确的最优参数。本文中使用的数据集取自动循环次数为40次。初次设定gamma范围为0.001～0.1,C的范围为0.1～20,自动循环的网格搜索运行。迭代次数为1,2,16,24,32,40时的准确率如表4所示。由表4可知,在运行至第2次后,得到了98%的准确率。但本文进行了40次的循环,这是因为在较高的准确率下,寻找更优参数的难度增加,为了确定最高准确率的可靠性,在后续的循环中得到准确率一致的情况下,可以认为得到了全局最高准确率。

图6 3组优化参数不同搭配的分类结果

针对一种数据集分类时,采用传统SVM分类器,需要调整两个参数的数值,运行时间约为10 min,实际应用不方便。先进行网格搜索方式确定最优参数的大致范围后,可以进一步通过自动迭代的方式求取最优参数精确数值。该方法准确率高,且求解方式便捷,整个求解时间仅为26.77 s,大大缩减了寻找最优参数的时间。

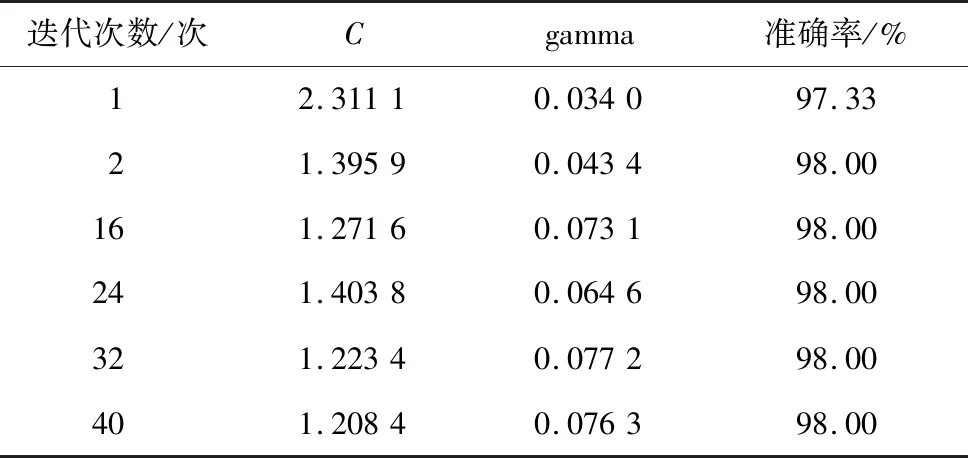
表4 取40次网格搜索结果中的5次结果

4 结 语

本文提出了一种SVM算法参数调整优化方法,且与手动调整参数以及网格搜索选择参数进行了实验比较研究。在选择最优参数(C,gamma)的过程中,以网格搜索法为基础,再通过在选定参数范围的基础上,采用自动迭代方式进行更精确的调参。实验结果表明,采用该方法,不仅分类的精度由原来的最高97.667%提高至98.00%,改进了学习性能,而且相较用原始方法调参使用10 min相比,该方法只用了26.77 s,大大提高了实际应用的效率。