基于遗传粒子群算法的FBG传感网重叠光谱的解调研究
夏 坤, 李志斌, 黄启韬, 刘 畅
(上海电力大学 自动化工程学院, 上海 200090)
相比于传统传感器,光纤布拉格光栅(Fiber Bragg Granting,FBG)传感器具有抗电磁干扰、抗腐蚀、复用能力强、传输距离远等特点,被广泛应用于电力、桥梁、隧道、航空航天等领域[1-2]。其原理主要是通过检测FBG传感器反射光谱的中心波长漂移量来反应被测物体的外部环境变化[3]。但在实际应用中,被测物体的体积都很大,需要用到大量的FBG传感器,所以需要将FBG传感器进行复用组网。目前,常用的复用组网技术主要包括时分复用技术、空分复用技术、波分复用技术等[4-6]。文献[4]基于马赫-泽德干涉仪解调器件,采用时分复用技术对FBG传感器反射光谱的中心波长进行检测。文献[5]采用空分复用技术,对FBG传感器进行组网,实现了对温度和应变的实时检测。文献[6]采用波分复用技术以及模拟退火算法增加了FBG传感器的使用数量,实现了对反射光谱中心波长的检测。但是,由于光源的带宽有限,如果使用的FBG传感器数量过多,会造成反射光谱发生重叠,因此上述的复用技术并不能很好地应用于实际工程中。
本文主要利用光谱形状复用技术,并采用遗传粒子群混合算法来识别反射光谱发生重叠时的中心波长,为因光源带宽而限制FBG传感器使用数量的问题提出了一种解决思路。
1 光谱形状复用原理
光谱形状复用技术主要是通过检测FBG反射光谱的形状来获取光纤光栅传感信息[7]。当采用光谱形状复用时,在遇到光纤光栅传感器的外部环境(温度、应变等)发生变化的情况下,仅仅光纤光栅反射光谱的中心波长发生漂移,而光谱的形状并未发生变化,通过对反射光谱的识别就可以得到外部环境的变化量。
假设存在n个光纤光栅传感器,在正常工作的情况下,每个光纤光栅传感器的反射光谱标记为gi(λ)(0≤gi(λ)≤1;i=1,2,3,…,n),整个光纤光栅光谱复用系统的反射光谱可以表示为[8]
(1)
式中:Ri——第i个光纤光栅传感器的峰值反射率;
λBi——第i个光纤光栅反射光谱的中心波长;
N(λ)——复用系统中的噪声。
一般把R(λ)作为原始光谱。为了实现简化光谱计算的目的,对原始光谱进行重构,重构光谱为
(2)
式中:xBi——重构光谱的中心波长。
在光纤光栅光谱形状复用系统中,光纤光栅的反射光谱采用高斯函数[9]近似表示为
(3)
式中:ΔλB——光纤光栅的3 dB带宽。
若想知道原始光谱与重构光谱的区别,对式(2)和式(3)作方差处理[10-11]。所得结果为
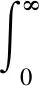
(4)
由式(2)~式(4)可知,当xBi无限趋近于λBi时,则f(xBi) 会无限接近于最小值,重构光谱无限接近于原始光谱。因此,通过求出xBi的大小,就可以得出原始光谱中每个光纤光栅反射光谱的中心波长。
2 遗传粒子群混合优化算法原理
遗传算法是通过模仿自然界生物进化机制发展起来的随机搜索方法,具有良好的全局搜索能力以及能自适应的控制搜索过程,但是遗传算法收敛速度较慢,局部搜索能力较差,并且其交叉和变异不具有记忆性[12]。粒子群算法虽然相对来说比较简单,方便实现,具有很强的简明鲁棒性,同时局部搜索能力很强,收敛速度也相对较快,但是粒子群算法容易早熟,具有很强的随机性,容易陷入局部极值点,影响算法的收敛性,全局搜索能力较弱[13]。
根据遗传算法和粒子群算法各自的特点,将两者进行结合改进,形成遗传粒子群混合算法。在算法初期,为了保证种群的多样性,利用遗传算法的交叉和变异特性进行优化,并且保留了全局搜索的特性。在算法后期,转到粒子群算法,强化其局部搜索能力,同时可以提高算法的收敛速度[14]。
遗传粒子群混合算法的具体步骤如下。
步骤1 初始化种群信息,设置算法初始参数值:初始种群N,交叉概率Pc,变异概率Pm,学习因子c1和c2,迭代最大步数L,随机赋值给粒子群的初始速度v0和初始位置x0。
步骤2 计算种群个体的适应度值,确定种群的初始化最优解。
步骤3 进行选择、交叉、变异操作:首先,根据步骤2所得出的适应度值,对当前种群使用轮盘赌法来执行选择操作;其次,对得到的新种群进行两两配对,通过使用两点交叉法来执行交叉概率为Pc的交叉操作;最后,对得到的新种群执行变异概率为Pm的变异操作。
步骤4 判断是否达到指定代数,如果达到则进入步骤5,如果没有达到则返回到步骤2。
步骤5 将遗传算法执行完之后形成的新种群作为粒子群算法的初始种群。
步骤6 计算每个粒子的适应度,根据初始位置的适应度,搜寻出初始化的个体最优解和全局最优解。
步骤7 根据粒子速度与位置迭代公式对粒子的速度和位置进行更新,公式如下
式中:vold,vnew——粒子速度迭代更新前后的值;
xnew,xold——粒子位置迭代更新前后的值;
c1,c2——学习因子,值为正;
r1,r2—— (0,1)的随机数;
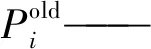
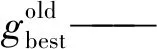
步骤8 判断是否达到指定代数,如果达到则进入步骤9,如果不满足则返回步骤6。
步骤9 输出最优解,结束算法。
遗传粒子群混合算法具体流程如图1所示。
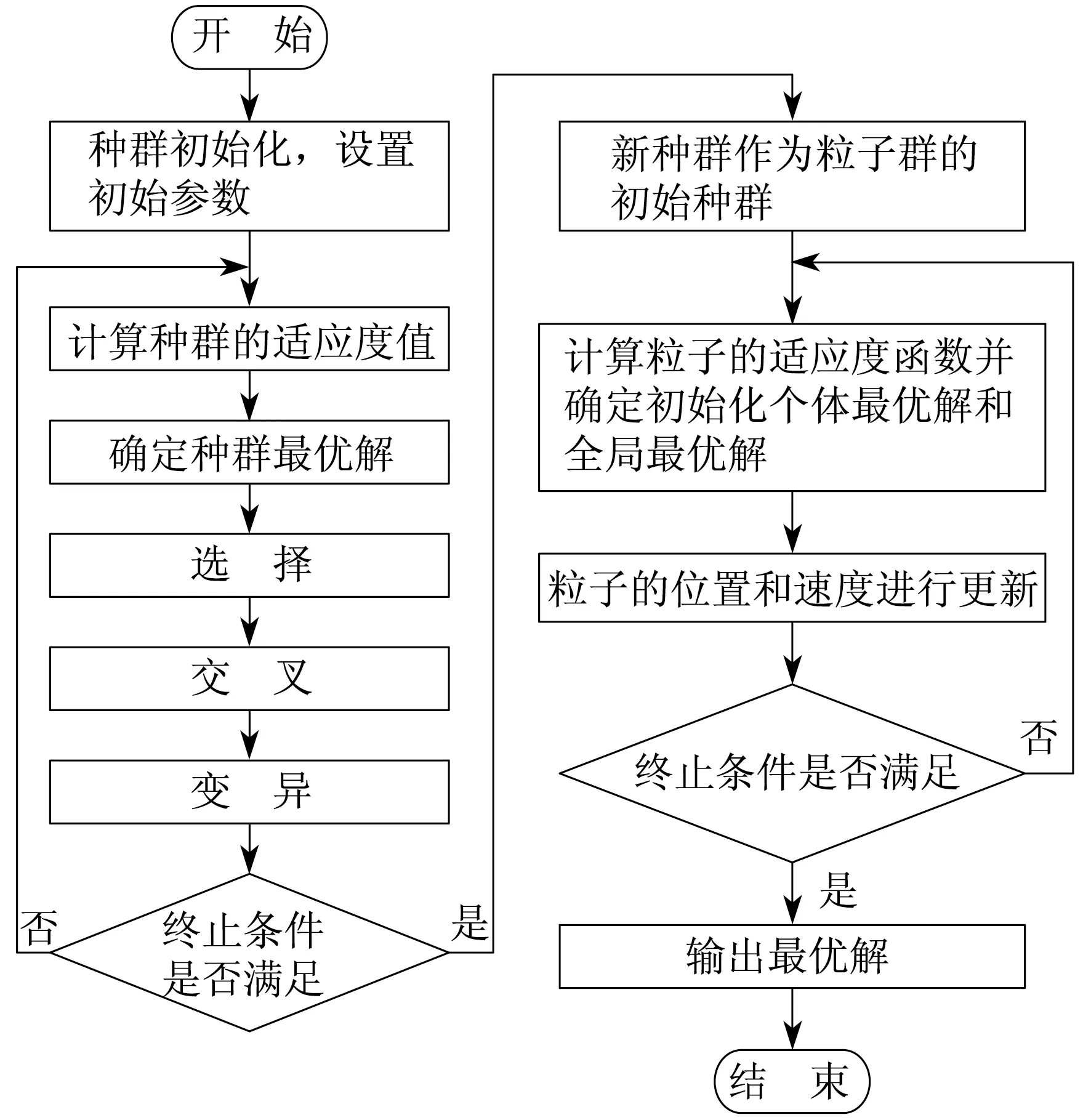
图1 遗传粒子群混合算法流程
3 实验原理及平台
本文所采用的实验原理如图2所示。光波由光源发出,经过FBG传感器反射回来穿过耦合器,进入到可调谐F-P滤波器,通过对可调谐F-P滤波器施加锯齿波扫描电压,来改变可调谐F-P滤波器的压电陶瓷的腔长,使其透射波长在一定的范围内进行周期性扫描。如果光纤光栅的外部环境发生变化,则会使光纤光栅的反射光谱的中心波长发生偏移。如果该波长在可调谐F-P滤波器扫描范围内,则光电探测器会检测到最大光强。由于可调谐F-P滤波器透射光波的波长与锯齿波电压呈线性关系,所以通过查询此时的锯齿波扫描驱动的电压值,就可以得到FBG传感器反射光谱的中心波长。
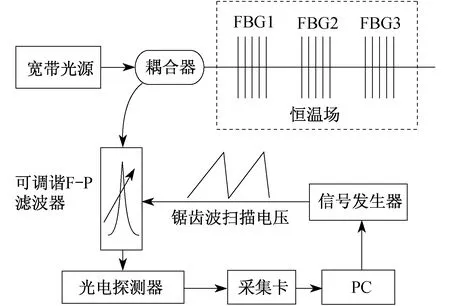
图2 实验原理
根据图2搭建的实验平台如图3所示。

图3 实验平台
整个系统由宽带光源、可调谐F-P滤波器、光电探测器、KNPGT-1光纤光栅传感器、耦合器等组成。其中,宽带光源采用由Fiberer公司的ASE宽带光源,其波长范围在600~1 700 nm,最大峰值功率为100 MW;可调谐F-P滤波器采用由美国Micron Optics公司研制开发的FFP-TF2可调谐滤波器,其自由光谱范围在99 nm之内,调谐电压在0~18 V之间,可在-20~80 ℃温度下工作;光电探测器采用的是Thorlabs公司生产的PDA 10CS-EC的铟镓砷光电探测器,可在700~1 800 nm波长段内工作;FBG传感器采用的是上海启鹏工程材料科技有限公司生产的KNPGT-1光纤光栅传感器,其反射率可达到99%。
4 仿真验证及分析
假设存在两个FBG传感器发生光谱重叠,根据式(4)构建光谱形状复用解调适应度函数为
(7)
由式(7)可知,g(xBi)的值非负,并且g(xBi)与f(xBi)成反比,满足算法适应度函数的要求。
假设这两个FBG传感器的中心波长分别取λB1=1 527.2 nm,λB2=1 527.6 nm。另外,假设这两个FBG传感器的反射率分别为R1=1,R2=0.8。为了实现这两个FBG传感器从部分重叠逐步到完全重叠的目的,可以通过对第1个FBG传感器的中心波长以每次0.2 nm的速度逐步增长到1 528.0 nm,并固定第2个FBG传感器的中心波长λB2保持不变。
在参数值保持一致的情况下,分别采用遗传粒子群混合算法、基本遗传算法、基本粒子群算法进行仿真。本次仿真选取的参数分别为:初始种群N=20,交叉概率Pc=1,变异概率Pm=0.1,学习因子c1=2.05,c2=2.05,迭代最大步数L=600。根据上述方式改变第1个FBG传感器的中心波长,对这3种算法分别进行5次运算,将仿真结果进行对比,得出两个FBG传感器中心波长的仿真结果如表1和图4所示。

表1 3种算法仿真得出的FBG传感器中心波长数值
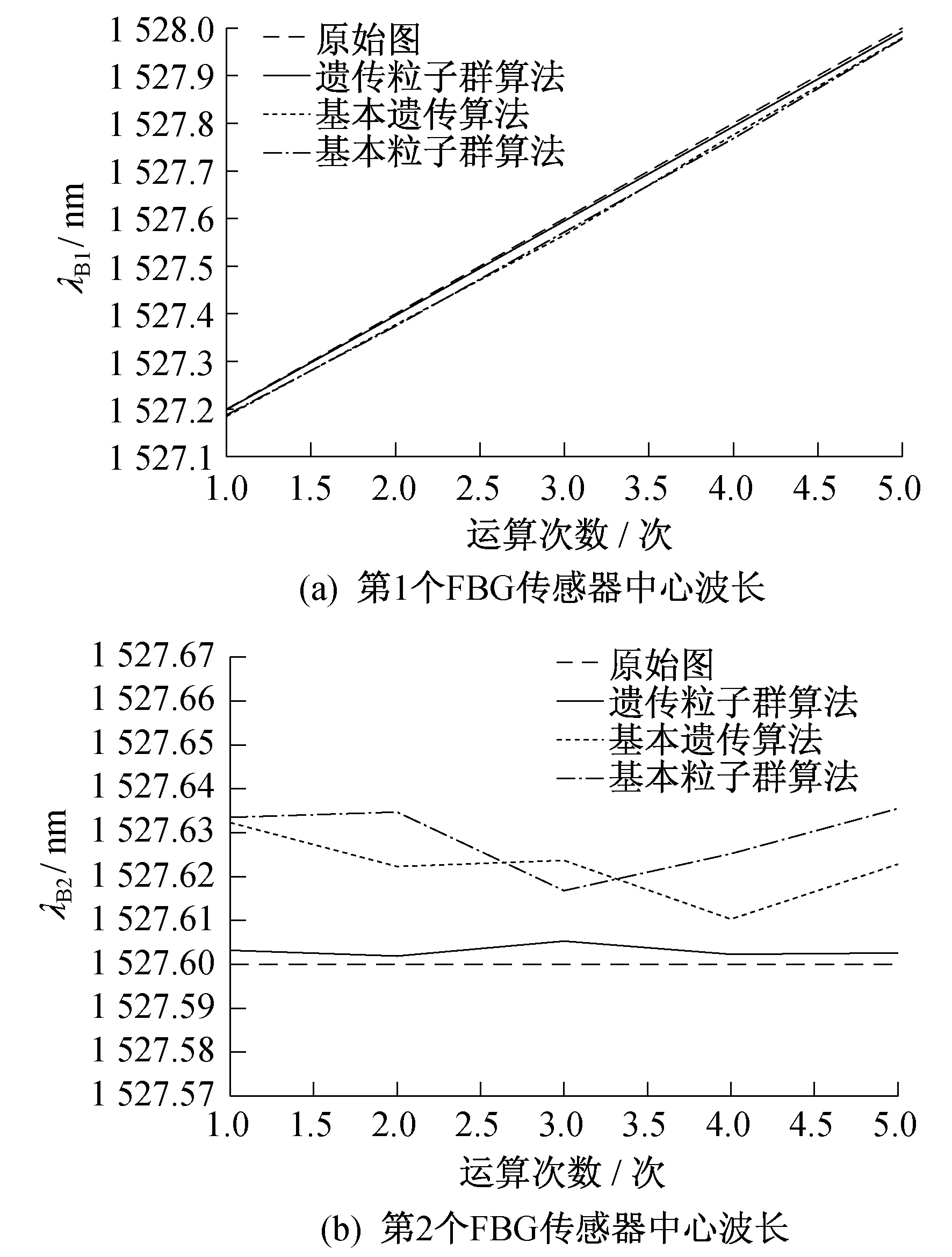
图4 FBG传感器中心波长的仿真数据折线
由表1可知,当两个FBG传感器的反射光谱发生部分重叠或是完全重叠时,在选取适当的计算参数条件下,这3种算法都能够识别出重叠光谱的中心波长,但是检测精度不同。通过基本粒子群算法和基本遗传算法识别出的光谱中心波长的误差范围基本上都在30 pm左右;而遗传粒子群混合算法的误差范围基本维持在5 pm之内,其仿真结果明显优于其他两种算法。通过图4中仿真数据与原始波长的差距,可以看出利用遗传粒子群混合算法仿真得出的波长更加贴近假设波长。
5 结 语
本文通过将遗传算法和粒子群算法进行结合,形成一种遗传粒子群混合优化算法,并将该算法应用到FBG传感器的光谱形状复用技术中,在FBG传感器发生光谱重叠时可对重叠光谱进行识别。通过仿真实验可知,该方法在识别重叠光谱的同时可保证识别误差范围在5 pm之内,明显优于基本遗传算法和基本粒子群算法的识别精度。为解决因光源带宽而限制FBG传感器的使用数量提出了一种可行方案。

