基于PJ模型的蒸发波导敏感性与雷达探测性能分析*

刘勇，张利军，朱庆林，马强

(1.中国人民解放军92941部队,辽宁 葫芦岛 125000;2.中国电波传播研究所,山东 青岛 266107)

0 引言

在海面探测目标时，主要使用的探测设备为雷达，由于对流层介质的不均匀性，雷达发射和接收电磁波会受到大气折射的影响，从而影响雷达探测的性能。蒸发波导形成的机理是海平面上的饱和水汽压上升到一定高度后锐减，导致大气折射指数在垂直梯度上呈现异常分布。蒸发波导高度是海洋蒸发波导重要的特征量，是表征波导强度的重要参数，也是确定蒸发波导对雷达装备、电子对抗装备影响的一个重要参量[1-9]。目前，通过关于蒸发波导模型的比较验证表明，PJ模型仍然为不失准确性的较佳候选模型[10]。

本文采用PJ模型计算蒸发波导的高度，对蒸发波导探测系统开展敏感性分析，根据蒸发波导环境下电磁波传输所满足的抛物线方程，并通过对电磁波的传输损耗计算，对雷达探测的距离进行预测。

1 PJ蒸发波导模型基本原理

Paulus-Jeske模型简称PJ模型，是早期成功被广泛使用的蒸发波导模型，PJ模型[8-9]通常使用海面以上一定高度(一般为距离海面6m)上的空气温度、相对湿度、风速、压强以及海表皮温度作为输入,计算蒸发波导的高度和其相关的波导参数。

引入位折射率Np，且假定满足相似理论，即：

(1)

式中：p0为大气压，取1 000 hPa；θ为位温；ep为位水汽压。

位折射率和大气折射率梯度之间满足：

(2)

式中：z为离海面高度，m。

当满足∂N/∂z<-0.157时出现大气波导，因此在∂Np/∂z<-0.125时出现蒸发波导，当位折射率垂直梯度等于波导形成的临界值bc=-0.125时，所对应的高度就是蒸发波导高度。假定引入的位折射率为相似参量，且满足：

(3)

式中:SNp为位折射率的垂直通量；ρa为空气密度；κ为卡门常数，取0.4；u*为摩擦速度；z0为动力粗糙度，在PJ模型中取z0=0.00 015 m；φ为普适函数。其中普适函数在稳定条件表达为

(4)

在非稳定条件下，采用KEYPS剖面的线性方程进行拟合，拟合的方程根的形式为

(5)

式中:L为莫宁奥布霍夫相似长度;常数α1,α2分别取α1=5.2，α2=4.5。

假定通量SNp随高度变化为常数，从海面积分到高度z有

(6)

ΔNp为测试高度和海面间的位折射率差，根据式获得湍动通量项为

(7)

将湍动通量项代入相似理论方程有

(8)

(9)

由于粗糙度z0较小，上式可近似表达为

(10)

式中，将普适函数表达式代入有

(11)

非稳定条件，蒸发波导高度为

(12)

式中:

(13)

(14)

当气海温差大于-1°时，Paulus基于海上实验也对波导高度进行了修正。仅仅改变气温，当气海温差等于0的蒸发波导高度大于气海温差等于-1°的蒸发波导高度，取气海温差为-1°蒸发波导高度，否则取实际气海温差的蒸发波导高度。

2 敏感性分析

2.1 气海温差敏感性分析

假设海面气压为1 012 hPa，海表面水温为25 ℃，海面相对湿度为80%，海面风速分别为5，10，15 m/s条件下，计算得到的蒸发波导高度随着海面气海温差的变化，如图1所示。

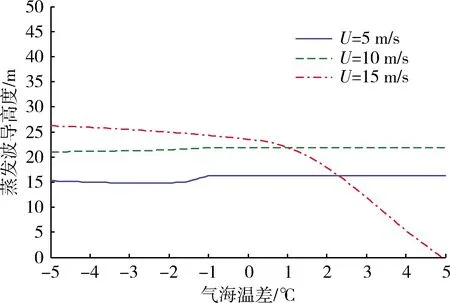
图1 蒸发波导高度随着气海温差的变化Fig.1 Evaporation duct height changes with the temperature difference between the gas and the sea

在低风速条件下，蒸发波导高度基本不变。而在高风速条件下，蒸发波导高度在气海温差小于0时基本不变，在气海温差大于0时，高度急剧下降。由于引入了人为的修正，因此该模型中不会出现蒸发波导高度随着气海温差增加而急剧增加的现象。

2.2 相对湿度敏感性分析

假设海面气压为1 012 hPa，海表面水温为15 ℃，气温为13 ℃(气海温差小于0，不稳定层结)，海面相对湿度为30%～100%，海面风速分别为5,10,15 m/s条件下，计算得到的蒸发波导高度随着相对湿度的变化，如图2所示。

图2 蒸发波导高度随着相对湿度的变化(不稳定层结)Fig.2 Evaporation duct height as a function of relative humidity (unstable layer junction)

假设海面气压1 012 hPa，海表面水温为20 ℃，气温为20 ℃(气海温差等于0，中性层结)，海面相对湿度为30%～100%，海面风速分别为5,10,15 m/s条件下，计算得到的蒸发波导高度随着相对湿度的变化，如图3所示。

图3 蒸发波导高度随着相对湿度的变化(中性层结)Fig.3 Evaporation duct height as a function of relative humidity (neutral layer junction)

假设海面气压1 012 hPa，海表面水温为15 ℃，气温为16 ℃(气海温差大于0，稳定层结)，海面相对湿度为30%～100%，海面风速分别为5,10,15 m/s条件下，计算得到的蒸发波导高度随着相对湿度的变化，如图4所示。

可以看出：不论何种层结，蒸发波导高度随着湿度的变化改变十分剧烈。随着相对湿度的增加，蒸发波导高度迅速降低。

2.3 传感器误差引起的综合敏感性分析

温度、湿度、风速传感器一般存在测量误差，假定如下常用的测量误差：①温度测量误差：±0.2 ℃；②相对湿度测量误差：±5%；③风向测量误差：±5°；④风速测量误差：±0.3 m/s(≤10 m/s)，±0.03 m/s(>10 m/s)；⑤气压测量误差：±0.5 hPa；⑥海温测量误差：±0.2 ℃。在其他水文气象条件不变的情况下，通过使某一要素产生随机扰动，可以研究单一要素随机扰动对蒸发波导高度诊断分析的影响；通过使多个要素同时产生随机扰动，可以研究多个要素同时随机扰动对蒸发波导高度诊断分析的影响；由此可以分析判断海面水文气象要素探测误差对蒸发波导高度诊断分析误差的影响。基于蒙特卡罗仿真运行10 000次，表1～3分别给出了稳定、不稳定、中性条件下传感器单一要素测量误差以及所有要素测量误差对蒸发波导高度的敏感性分析。由表中数据可以看到：相对湿度是影响蒸发波导高度的关键因素，其次是风速，然后是气海温差。在PJ模型中由于假定气压为1 000 hPa，因此模型与气压取值无关，其测量误差不影响蒸发波导高度预测。3种条件下，综合考虑传感器的测量误差，蒸发波导高度预测相对误差分别为14.3%，4.22%，8.05%。如果传感器的相对湿度测量进一步减小，则可以显著减小蒸发波导高度的预测误差。

图4 蒸发波导高度随着相对湿度的变化(稳定层结)Fig.4 Evaporation duct height as a function of relative humidity (stable layer junction)

表1 稳定性条件传感器测量误差对蒸发波导高度影响Table 1 Stability condition sensor measurement error on the evaporation waveguide height

表2 不稳定性条件气象要素扰动对蒸发波导高度影响Table 2 Unstable conditional meteorological element disturbance influence on the evaporation waveguide height under

表3 中性条件气象要素扰动对蒸发波导高度影响Table 3 Neutral conditional meteorological element disturbances influence on the evaporation waveguide height

3 蒸发波导对雷达探测影响的模型及验证

3.1 蒸发波导环境中电波传输损耗及抛物型方程电磁波在空间传输过程中，往往会伴随着衰减现象的发生，传输损耗可以度量电磁波在传输过程中形成的衰减。电磁波通过蒸发波导后所产生的损耗，即在自由空间的传输损耗上引入蒸发波导的衰减因子。

当收发雷达天线的极化互相匹配，并与对应负载相匹配时，此时雷达的接收功率可表示为

(15)

式中：S为坡印廷矢量；Ae为接收雷达天线的有效面积；Pt为发射雷达天线的输入功率；Gt为发射雷达天线的增益；Gr为接收雷达天线的增益；λ为自由空间内的电波波长。

自由空间的传输损耗可表示为

(16)

忽略设备因素的影响，路径传输损耗Lb表明传输媒质中的功率传输情况，即

Lb=Lbf-A.

(17)

基于抛物线方程，蒸发波导中的电磁衰减因子A可表示为

(18)

Barrios,Dockery和Kuttler等人通过使用抛物型方程对蒸发波导中的传播问题变成开域边界值的求解问题[11-14]，能够解决在蒸发波导中存在的折射指数分布不均的问题。运用抛物型方程能够有效地解决电磁波在蒸发波导环境中传播问题。抛物线的近似方程：

(19)

式中:n为大气折射指数；ae为地球半径；x为目标距离球地面的距离；z为目标距离球地面的高度；根据给定的初始值及对应的边界条件通过裂步傅里叶数值计算，可以得出电磁波在蒸发波导中的传播损耗空间分布。

3.2 蒸发波导中的雷达性能评估验证

将设备的实际损耗和海面的环境导致的损耗考虑在内，雷达对待测目标的最小可检测信号功率Simin和雷达的接收功率Pr分别为[15]

(20)

(21)

式中：k=1.38×10-23(J/K)，T=T0=290 K，Bn为接收雷达的带宽(MHz)，和脉冲宽度τ的对应关系为：Bn≈1/τ；D0为接收雷达的输出端的最小信噪比，其值为：D0=(S0/N0)min，其值由探测概率Pd和虚警概率Pf共同决定的。Pr为雷达的接收功率，Pt为雷达的发射功率，G为雷达的增益；σ为雷达散射截面积；R为目标斜距；F为相对自由空间的传播因子；Ls为系统的综合损耗(dB)。

当Pr=Simin时，可求得雷达检测待测目标的最大作用距离。基于路径传输损耗表示的接收功率表达式为[16]

Pr=81.55+10lg(Ptσf2)+2G-2Lb-Ls.

(22)

其中路径传输损耗用下式表达：

Lb=Lbf-20lgF=32.45+20lgf+20lgR-20lgF.

(23)

由式(22)也可得用接收功率表示的电磁波单程传输损耗，即：

Lb=0.5×(81.55+10lg(Ptσf2)+2G-Ls-Pr).

(24)

雷达对待测目标的探测性能体现在待测目标的回波功率，因此可设定雷达的最小可检测信号门限为

T=0.5×(81.55+10lg(Ptσf2)+2G-Ls-Smin).

(25)

即Lb≤T与Pr-Simax≥0是等价的，当Lb≤T时，待测目标能够被雷达检测到，因此雷达能够检测待测目标的最大距离Rmax为Lb正好等于最小检测门限时的值，雷达检测该目标的最大作用距离Rmax可表示为

(26)

式中:A为蒸发波导环境下计算的传播因子。从实质上来看，与雷达方程中的常用的F传播因子一致。为区分特定环境下的传播因子，此处用A来表示。2017年4月开展的某次试验中，某型雷达针对低空目标的发现距离为46.6 km。基于上述雷达性能评估算法给出的预测距离为45 km，说明了该算法的有效性。

4 结束语

蒸发波导高度随气海温差、海面风速、相对湿度变化而变化。小风速下，蒸发波导高度随着气海温差增加而有小幅度升高；大风速下，蒸发波导高度在稳定条件下随着气海温差增加而显著下降，不稳定条件下有小幅度下降。海面相对湿度是影响蒸发波导高度变化的最敏感因子，不论何种条件蒸发波导高度基本随海面相对湿度增大而减小。给定通常的传感器测量误差，蒸发波导高度预测的相对误差分别为14.3%，4.22%，8.05%。若传感器测量的相对湿度误差进一步减小，则蒸发波导高度预测将更为准确。通过抛物线型方程对电磁波在蒸发波导中的传播损耗进行了模拟，并在雷达探测性能的评估方法中充分运用了蒸发波导的环境因素，模拟计算了雷达在蒸发波导中的探测距离，为雷达系统在海面探测上的提供了重要的参考价值。