城市道路交通管控时间与区域长度控制方法
韩 直,张 杰,韩嵩乔
(1.重庆交通大学交通运输学院,重庆 400041,2.招商局重庆交通科研设计院,重庆 400041,3.东北师范大学数学与统计学院,长春 130024)
随着交通运输业的发展,城市道路交通拥堵现状愈发严重,交通诱导管控显得越发必要,因此,对于管控时间与管控区域的选取也越来越重要。
传统管控时长与管控范围的选取主要根据道路交通量、速度、密度三个参数进行判别选取,但由于交通量、速度、密度是相互关联的,并不是相互独立的;无论速度与密度的关系是满足Greenshields所提出的直线线性关系,或是Greenberg所提出的对数模型,亦或是Underwood所提出的指数模型[1],当知道速度、密度的关系时,则知晓三者间的关系,所以在实际应用中,无论用速度、密度或交通量中的一个或多个对交通状态进行判别,其实均为单参数对交通状态进行判别,因此,所选择的管控时长与管控范围不准确,所以有必要探讨交通流在时间和空间上的关系,以此来精确计算管控时长与管控区域的长度。
在道路交通诱导管控研究中,对于管控范围的选取,多数研究[2-4]均采用不同的方法确定道路网络中的关键节点,以此通过节点来确定管控区域。此种选取方法可以得到管控区域的范围,但不能得到管控区域的精确长度。在道路交通流时空特性研究中,多数学者利用交通流的时空特性,建立了短时交通流预测模型[5-7],有效地对交通流进行了预测;部分学者[8-9]分析了不同等级道路交通流的时空特性;杨婷等[10]利用动态时间占有率分析了交通拥堵的效率;董春娇等[11]利用时空特性对道路网进行了动态的划分。现有的研究结果中,多为利用道路网的时空特性进行相关的研究,缺少对交通流在时间上与空间上关系研究。为了更好地从时间与空间上研究交通流的特征以及确定交通管控时长与管控范围长度,本文从时间占有率与空间占有率的定义出发,定义了累计时间占有率与累计空间占有率,证明累计时间占有率与累计空间占有率具有等效性,基于此,对累计时间占有率与空间占有率在一定时间段内积分,建立交通流时空模型,得出相关参数的关系,并探讨了该模型的主要用处,以期对交通管理提供参考。
1 累计时间占有率与累计空间占有率的关系
1.1 累计时间占有率与累计空间占有率定义
时间占有率[1](Rt)是指在观测时间内,所有车辆的车身长通过道路某断面所占用时间(ti)之和与总观测时间(T)之比。空间占有率[1](Rs)是指在某观测瞬间,路段上所有车辆的车身长(li)之和与路段长度(L)之比,
(1)
(2)
由于时间占有率表示的是在一段时间内某一断面的道路拥挤情况,空间占有率表示的是某一瞬间一段道路上的道路拥挤情况,两者条件不同,无法进行比较,故应将时间占有率与空间占有率放在同一维度进行比较。
将累计时间占有率(Qct)定义为在一定观测时间内,所有车辆的车身长通过特定长度道路某一断面所占用时间之和与总观测时间之比;将累计空间占有率(Qcs)定义为在观测时间T内,进入路段所有车辆的车身长之和与路段总长度之比,其中,路段总长度为单条路段长度乘以车道数(m)。即:
(3)
(4)
1.2 累计时间占有率与累计空间占有率关系
假设T时间内,进入长度为L的道路上有N辆车,未有车辆驶出,车道数为m,第i辆车的车辆长度为li,速度为Vi。根据累计时间占有率的定义可得,在T内,L长的道路上,累计时间占有率为
(5)

(6)
式(6)中:K为多车道交通密度,即所有车辆随机分配在m条车道时,此状态下道路上的交通密度;vs为区间平均车速。同理,在T内,L长的道路上,累计空间占有率为
(7)
(8)
式中:K′为单车道交通密度,即所有车辆都集中在一条车道时,此条道路上的交通密度。由式(4)、式(6)可得,在一定条件下,累计时间占有率与累计空间占有率具有等效性,即:
Ocs=Oct
(9)
2 数学模型
2.1 交通流的时空关系模型
由式(9)可得,累计时间占有率与累计空间占有率具有等效性,故在T内分别对累计时间占有率与累计空间占有率积分。对累计时间占有率积分得:
(10)
在道路行驶的车辆速度Vi的倒数与行驶时间t存在一定的函数关系,即:
(11)
式(11)中:Vi为第i辆车的车行驶速度,将f(t)i通过泰勒公式展开得:
f(t)i=a0i+2a1it+3a2it2+…+(n+1)anitn
(12)
令:

(n+1)antn
(13)
则:
(14)
式中:aj为待定系数,且aj与道路等级相关;n的取值与道路等级相关。
由式(8)~式(12)可得:
(15)
对累计空间占有率积分得:
(16)
式(16)中:Q为T内的平均交通量。
由累计时间占有率累计空间占有率的等效性和式(15)、式(16)可得:
(17)
由上述推导可得Q、T、m、L之间的关系,在实际应用中,可根据具体的应用场景,确定Q、T、m、L代表的具体含义。
2.2 讨论
采取控制变量法,对式(17)进行求导,并根据求导结果进行讨论。
此模型可用于交通管控,则Q可代表管控时间段内平均交通量,T可代表管控时间,L可代表管控区域长度,m为管控区域道路的车道数,利用此模型,可在管控时间确定时,精确地计算出管控区域长度,当管控区域长度确定时,精确地计算出管控时间。由表1可知,对于交通管控而言,当管控时间T一定时,平均交通量Q增加时,需管控更多的区域L对交通量进行分流;L一定时,当平均交通量Q很小时,无需进行交通管控,当平均交通量Q增加到某一阈值时,需进行管控,且平均交通量Q越大,需管控的时间T也越长;Q一定时,当管控时间T增加时,应管控的区域L也应增加,但不能一直增加,存在最佳的管控时间T与管控区域L。

表1 Q、T、L相关关系Table 1 Correlation of Q,T,L
3 实例验证
通过调查重庆内环快速路(东环立交-人和立交)得到该道路管控时间为早上8:00—10:00,并选取该时段的路段流量(间隔为5 min)以及平均速度(间隔为5 min)进行模型验证。将调查数据汇总并整理如表2。
对表2中平均速度进行倒数:式(18)并通过多元线性回归方法进行函数拟合:式(19)在要求内得出速度倒数与时间、平均交通量与时间关系如图2、图3所示。

表2 调查数据Table 2 Survey data
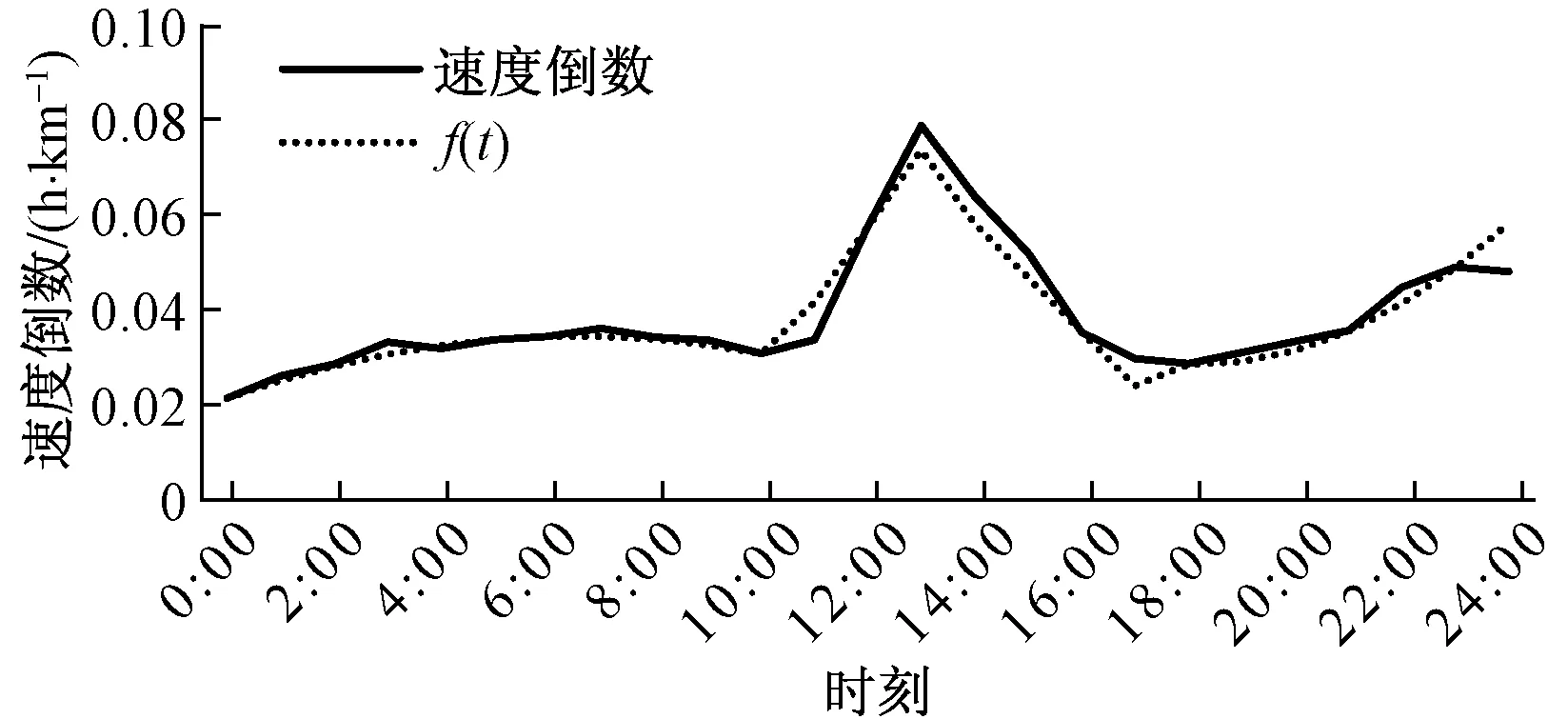
图2 速度倒数拟合关系图Fig.2 Reciprocal velocity fitting diagram

图3 平均流量拟合关系图Fig.3 Average flow fitting diagram
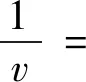
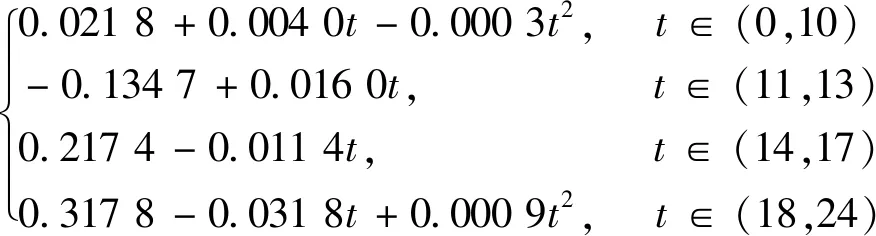
(18)
Q(t)=
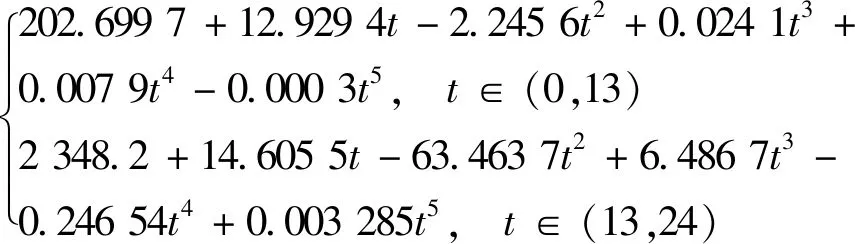
(19)
对累计时间占有率及累计空间占有率在T内进行积分得:
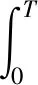
(20)
将上述数据代入(20)得出如表3所示结果。
由表3可得,在保持原有管控方式与时间不变的情况下,应管控区域长度为4 846 m,实际管理3 300 m,造成了管控资源的浪费;在保持原管控区域长度不变的情况下,应将原管控时长2 h,变为1.2 h,避免管控资源的浪费。

表3 结果分析Table 3 Result analysis
4 结论
首先,通过定义累计时间占有率与累计空间占有率,得出道路交通流的时空等效性,并建立了道路交通流的时空关系模型;其次,探讨并得出基于交通流的时间变化特征,可精确的计算出管控时间范围与管控区域长度;最后,通过实例验证了道路交通流时空关系模型的有效性,得出在重庆内环快速路(东环立交-人和立交)上,保持原管控时间不变时,应将管控区域扩大至4 846 m;保持管控区域不变,应将管控时间减少至1.2 h。

