基于三阶Teager能量算子的轴承诊断技术研究

叶 浩，高晓蓉，邱春蓉，李金龙

（西南交通大学 光电工程研究所，成都 610036）

大多数机械系统的操作都是基于角运动到其他运动的转换，滚动轴承在这一转换过程中起着至关重要作用[1]。作为常用的机械部件，轴承承担着很大的负担，由于轴承恶劣的操作环境，使其成为最容易发生故障的机械元件之一，因此对滚动轴承的故障诊断显得尤为重要。

在诊断滚动轴承故障方面，提取和选择故障特征发挥着主要作用，此步骤在一定程度上影响故障诊断的精确性[2-3]。对于信号的瞬态特征，Teager能量算子（TEO）具备一定增强效能。不同于常规的能量算子，TEO 在计算能量时需要考虑频率这一项[4]。因为冲击特征有较高的频率，在振动信号中由故障所致的冲击特征可以被TEO 很好地提取出来，在提取故障特征方面具备适用性。基于声信号，刘晶等人[5]通过TEO 解调检测轮对轴承故障，同Hilbert 解调进行了比较，证实此方法具备有效性。Li 等人[6]提出了一种通过相关性分析的面向独立的变模态分解（VMD，Variational Mode Decomposition）方法，自适应地提取轮对轴承的弱复合故障特征，克服了信息丢失和过分解的问题，实现了较为准确的故障诊断。陈刚等人[7]借助经验模态分解（EMD，Empirical Mode Decomposition）对轴承的振动信号实施分解处理，对含信号主要信息在内的本征模态函数（IMF，Intrinsic Mode Function）展开包络分析，由此有效地完成诊断识别故障轴承目的。Liu 等人[8]使用TEO 提取轴承故障引起的周期性冲击，并用小波包降低Teager 能量噪声，提取内外圈故障特征频率及谐振频带能量与Teager 频谱中总能量的比率为特征向量训练Elman 神经网络，检测出了变化条件下的轴承故障。

针对处于强背景噪声环境中的低信噪比信号，因过高的噪声干扰性，大多会淹没表征故障信号的不正常冲击特征，TEO 虽然一定程度上能增强信号冲击特征，但仍然不能大概率准确地提取出故障的特征频率。

因此本文在传统的二阶TEO 基础上进行改进，提出三阶TEO 来提高对低信噪比的滚动轴承的故障诊断能力。

1 改进的Teager能量算子

1.1 Teager能量算子

对于任一连续时间信号 ，Teager 能量算子ψ的表达式为[9-10]：

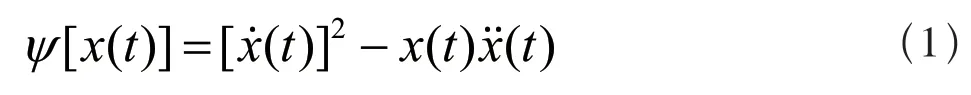
其中，(t)和(t)分别为信号x(t)相对于时间t的一阶和二阶微分。

文献[4]中已证得TEO 能够跟踪振动系统的总能量E。对于离散的时间信号x(n)，将微分替代为差分，则TEO 变为：

由式（2）可知，要想计算离散时间信号x(n)的TEO，只需知道每一时刻n处的3 个样本数据即可。

1.2 改进的Teager能量算子

由于轴承的工作环境中存在较大的噪声，而传统TEO 计算的阶次只是二阶，抗噪性能不强，因此本文提出三阶TEO 替代二阶TEO。针对离散时间信号的三阶TEO 定义如下：

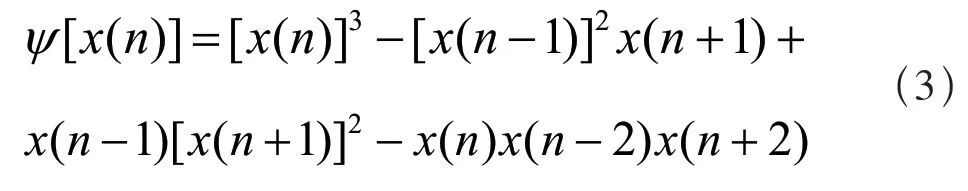
三阶能量算子的定义是在保证数学对称性的前提下，由二阶TEO 推导得到。相较于常规二阶TEO，在计算方面，三阶TEO 所应用的对称样本数据通常为5 个，因此三阶TEO 在时间分辨率上能更好地分辨信号瞬时变化，并检测出信号中更多的瞬时冲击成分。

1.3 改进的Teager能量算子诊断流程

考虑到在振动信号的采集过程中有强背景噪声的干扰，采集到信号的冲击特征被淹没在噪声当中，提出改进的三阶Teager 能量算子滚动轴承诊断方法。三阶Teager 能量算子故障诊断过程，如图1 所示。（1）通过三阶TEO 完成振动信号瞬时总能量的求解，自能量角度方面提升信号的瞬时特征，使信号内冲击成分突出。（2）对求解所得TEO 信号实施傅里叶变换处理，在频域上分析信号。（3）对三阶TEO 谱内核心频率成分同轴承各元件故障特征频率展开对比，以此来对故障轴承的故障类型进行评估。

图1 三阶Teager能量算子故障诊断流程

2 仿真信号验证

2.1 构造仿真信号

为了验证该方法是否有效，先完成存在故障轴承模拟信号的构建，再以此开展仿真测试。设此模拟的故障轴承信号对应以下表达式：

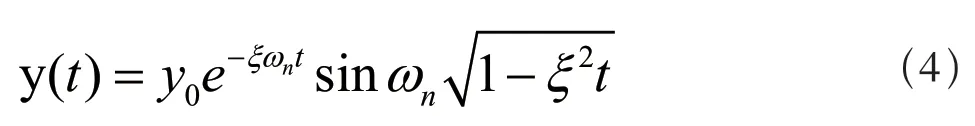
其中，位移常数y0=1，阻尼系数ξ=0.1，共振频率fn=3 000 Hz，角频率ωn=2πfn，脉冲故障的重复周期、特征频率、采样频率（fs）、采样点数依次为0.02 s、50 Hz、30 kHz、8 192。

在上述仿真故障信号基础上加入随机白噪声，使得含噪信号的信噪比为-4.03 dB，之后，分别用快速傅里叶变换（FFT， Fast Fourier transform）频谱、Hilbert 包络谱、二阶Teager 能量算子谱和三阶Teager 能量算子谱对该含强噪声的故障振动信号作分析，仿真信号分析结果，如图2 所示。

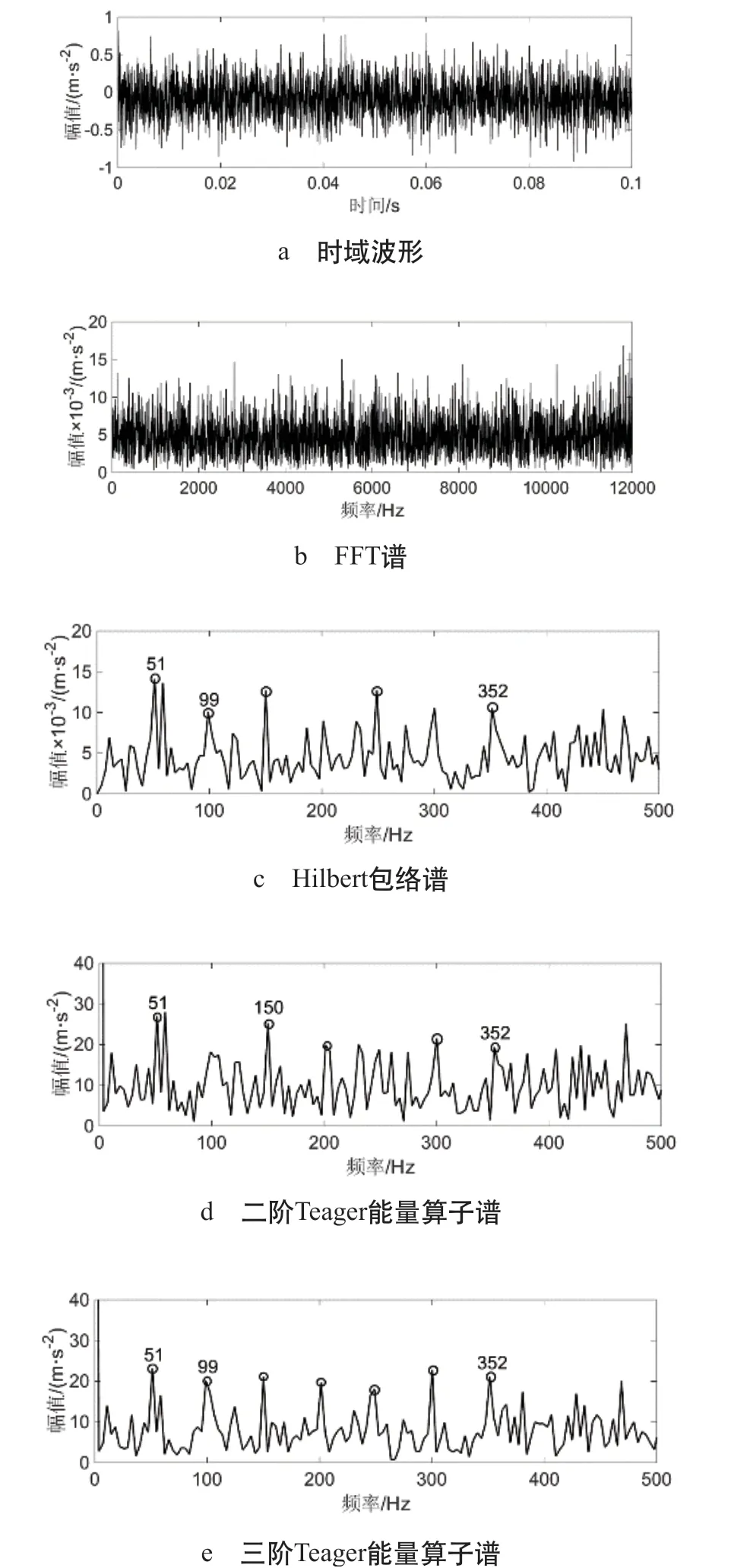
图2 仿真信号分析结果

2.2 结果分析

（1）由图2a 时域信号波形可知，通过将强噪声施加于仿真信号进行早期弱故障的模拟，噪声可于较大程度上淹没表征故障的冲击信号，导致信号的冲击特征不易识别。（2）图2b 仿真信号频谱中，由于冲击信号的特征频率与其倍频、转动频率及其倍频之间产生调制，加上强背景噪声引起的干扰，虽然在频谱中可以看到显著的频率成分，但这些分量都是干扰频率，不能反映轴承的故障信息。（3）在图2c 包络谱中，虽然能识别到部分故障频率及其倍频，但存在大量干扰频率与峰值频率混叠，难以准确识别故障频率。（4）图2d 二阶Teager 能量算子谱中，强噪声的干扰使得故障信号的冲击特征难以凸显，对故障频率的识别很困难。（5）图2e 所示三阶Teager 能量算子谱内，呈现出明显的故障信号冲击特征，可以十分清晰地对故障特征频率的倍频和基频成分加以识别，且可压制其它噪声频率干扰至较小范围。此次研究提及的三阶Teager 能量算子谱可使故障冲击特征增强，能够提高滚动轴承的故障特征频率提取的精准度，对于低信噪信号，此方法同样可高效提升其故障冲击特征。

3 实验数据分析

3.1 实验平台

为了对所述方法是否可用于测试平台进行验证，把以上方法用于开展高速列车的轮对轴承方面相关故障诊断研究。滚动轴承基本参数，如表1 所示。为了模拟滚动轴承各元件的局部损伤，在轴承的外圈用电火花加工一个宽约2 mm、深约0.1 mm 的凹坑，在单个滚子上加工一个宽约2 mm、深约0.2 mm 的凹坑。

表1 滚动轴承基本参数

滚动轴承测试平台，如图3 所示。实验中，加速度传感器设置在轴承的外圈，电机转速设定为110 r/min（外圈）和128 r/min（滚动体），采样频率为51 200 Hz。根据滚动轴承的参数，分别计算各元件的故障特征频率，如表2 所示。

图3 滚动轴承测试平台

表2 滚动轴承元件的故障特征频率 单位：Hz

实验中采集系统的以太网机箱为NI cDAQ-9181，如图4 所示。采集板卡为NI 9205，如图5 所示。通过NI MAX 实现对振动信号的采集，使用Matlab对采集到的振动信号做诊断处理，实现对动车组轴承故障的故障诊断，系统的采集界面，如图6 所示。

3.2 外圈故障信号分析

图4 以太网机箱

图5 采集板卡

图6 系统采集界面

对外圈故障轴承的振动信号与仿真信号相同的信号进行分析，外圈信号分析结果，如图7 所示。实验中使用的轴承故障程度较轻微，且实验环境中存在一定的背景噪声。（1）难以在图7a 时域波形图中，观察到信号的冲击特征。（2）图7b 频谱图中峰值频率杂乱无章，轴承外圈的故障特征频率被淹没在噪声中，无法识别。（3）图7c 所示包络谱内对故障特征频率，可提取到其基频与三倍频，未见突出的峰值频率，同时因二倍频混叠干扰频率，准确提取无法实现。（4）图7d 所示二阶Teager 能量算子谱内，因高强度噪声的干扰，故障特征频率被干扰频率所淹没，不易实施故障识别。（5）图7e 所示三阶Teager 能量算子谱内，明显呈现出峰值频率接近于

轴承故障特征频率，最高可获得故障频率的三倍频，显示出更具直观性与明显性的故障特征。由于存在实验误差，实测故障频率与理论频率并不完全一致，但在比较小的误差范围内。这说明了三阶Teager 能量算子谱方法在诊断轴承外圈故障时的有效性。

3.3 滚动体故障信号分析

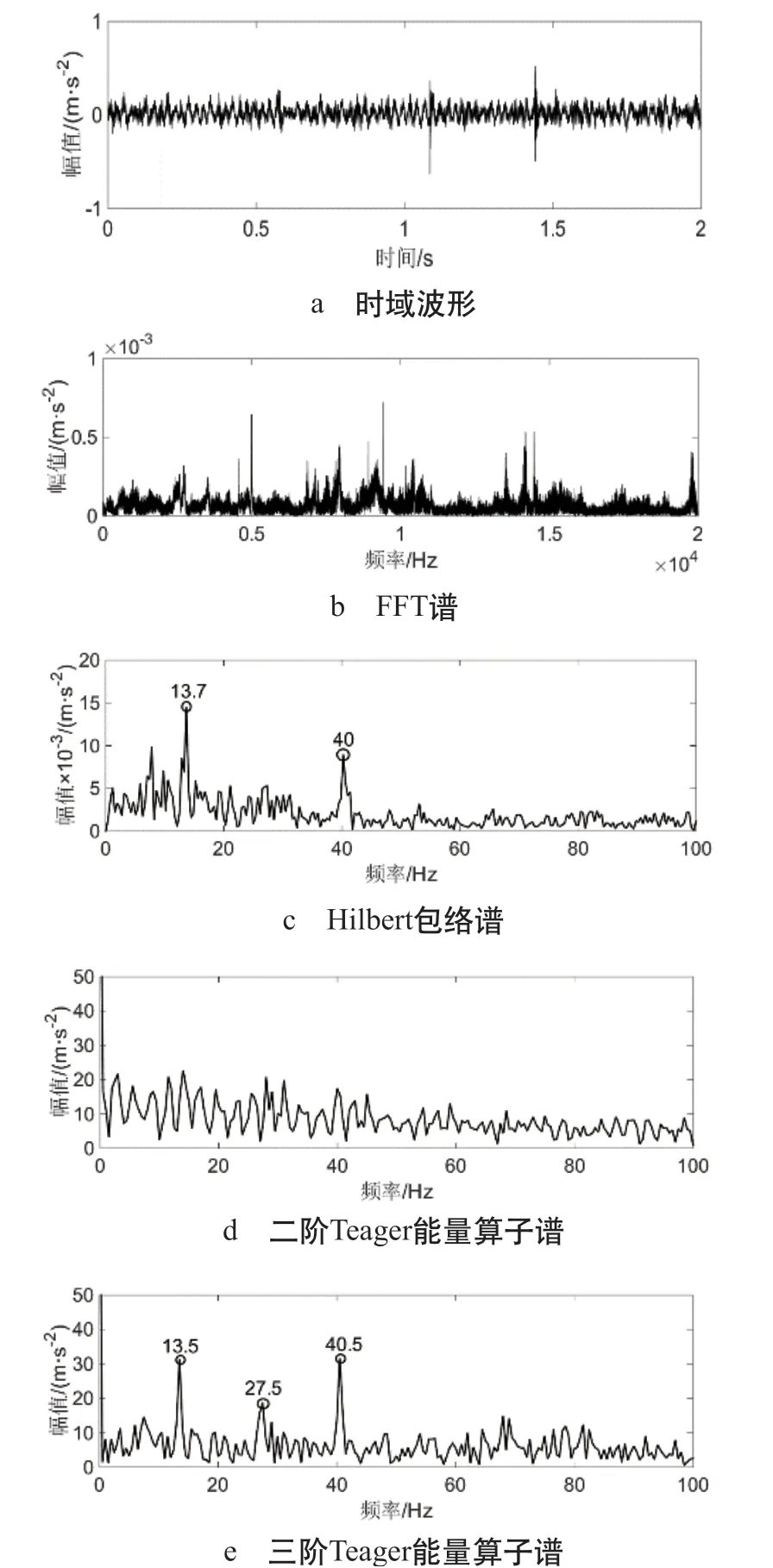
图7 外圈信号分析结果

方便对分析处理后的结果考虑，对轴承滚动体时域信号采取归一化处理。滚动体信号分析结果，如图8 所示。（1）图8a 的时域波形中能看到较为明显的冲击信号，说明轴承发生了故障。（2）图8b 的原始信号傅里叶谱图中能看到多条较为明显谱线，但都不能正确反映滚动轴承的故障特征。（3）对于此故障特征频率，图8c 所示包络谱内可提取其基频、二倍频与三倍频，噪声频率的干扰依然存在。（4）图8d 所示二阶Teager 能量算子谱内，因存在干扰频率，不能进行轴承故障的特征频率及其任一倍频的提取。（5）在图8e 三阶Teager 能量算子谱中，峰值频率与轴承故障特征频率8.0 Hz 的偶次倍频相对应，且倍频阶次连续，高达7 阶，且频谱信噪比高，由此可以准确诊断该轴承的滚动体出现了故障。

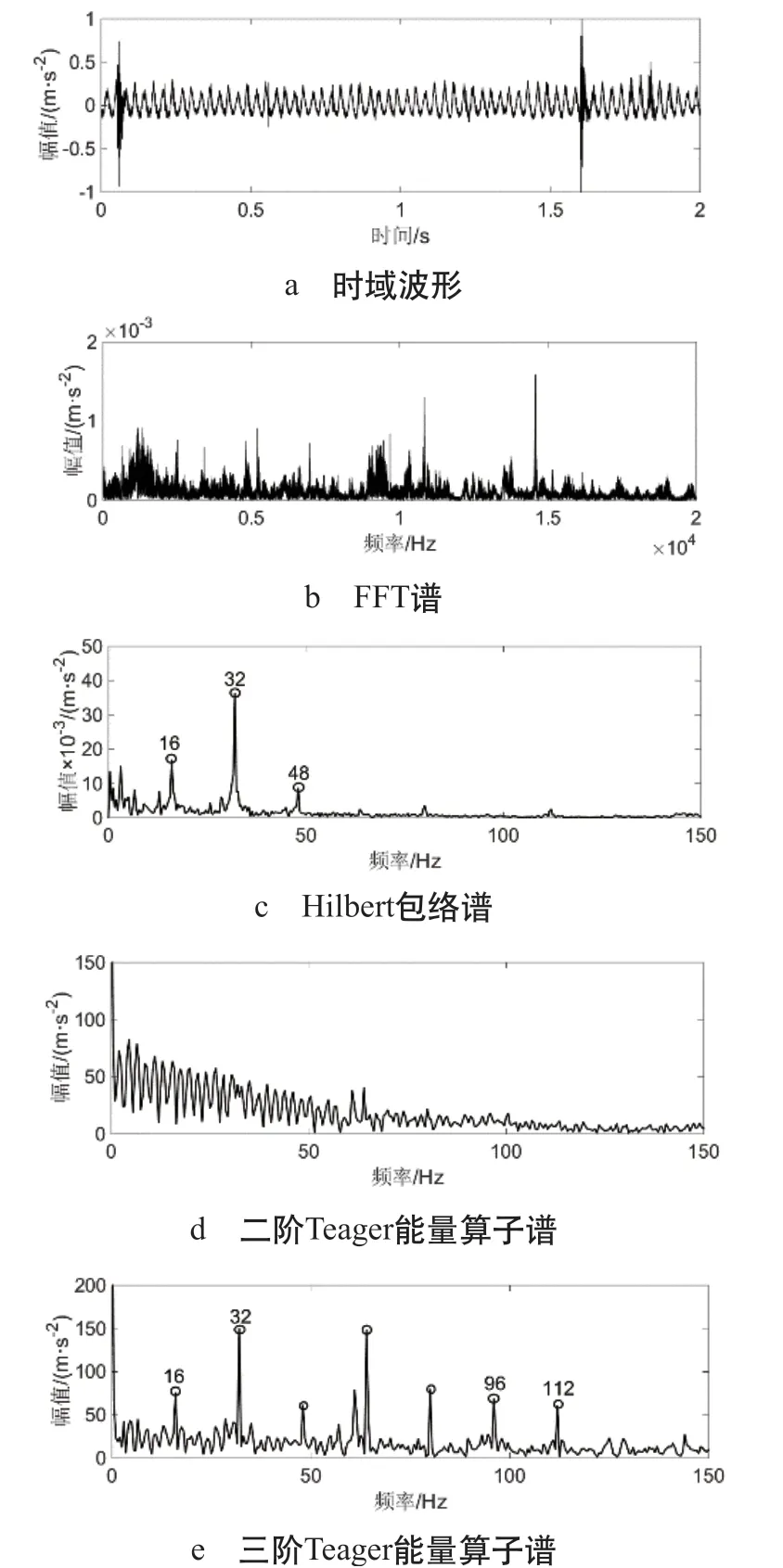
图8 滚动体信号分析结果

4 结束语

（1）对于设备的安全运行而言，滚动轴承的初期微弱故障诊断起着关键性作用，然而强背景噪音会淹没信号的冲击成分，采用包络谱分析和传统二阶Teager 能量算子解调分析难以从干扰中有效提取轴承早期微弱故障特征。

（2）采用三阶Teager 能量算子计算产生信号所需的瞬时总能量，很大程度地突出了冲击信号的瞬态峰值特征，并结合傅里叶变换作频谱分析能够有效提取出轴承早期微弱故障特征。

（3）受试验条件限制，本文所进行试验结果可能与实际工况情况存在差距。