上海市某人工地层冻结法施工模拟研究
许静怡,李泽垚,吴旭东,俞辰阳
(1.浙江工业大学 建筑工程学院,浙江 杭州 310014;2. 浙江省交通规划设计研究院有限公司,浙江 杭州 310013;3.同济大学 土木工程学院,上海 200092;4.浙江工业大学工程设计集团有限公司,浙江 杭州 310014)
0 前 言
COMSOL应用于冻结法,则是近些年来才兴起的,并获得了许多研究成果。秦爱芳等[1]运用COMSOL软件,研究了地铁旁通道采用冻结法施工冻结对周围环境的影响规律,以及冻结完成后开挖对周围土体产生的影响。高娟等[2]结合某地铁联络隧道水平人工冻结及开挖施工工程,采用热-流-固(THM)耦合理论,采用COMSOL有限元分析软件模拟了冻结过程中地层温度场、渗流场及位移场的变化规律,并研究了开挖后地层位移场的分布规律,认为实施人工冻结法对止水和抑制地层变形具有良好的效果。李婷婷[3]采用COMSOL软件对郑州地铁联络通道冻结法施工进行了多物理场耦合模拟分析,模拟施工对地表位移的影响以及联络通道开挖后对地表沉降的影响,并与实际工况进行对比,发现拟合效果较好,并为后续工程提供借鉴。和晓楠[4]应用COMSOL软件,对富含水地区冻结法施工进行了数值模拟,研究了冻结过程中温度场的发展规律以及冻结壁的形成情况,并与现场监测情况做了比对发现具有较好的一致性。
COMSOL数值模拟软件在冻结法施工多场耦合方面具有很好的适应性,故使用本软件对上海某工程联络通道冻结法施工进行温度-应力-渗流三场耦合分析,以得到具有普适性的模型。
1 计算模型
本文拟采用更为成熟的水热力耦合模型,其是在考虑水热耦合的基础上,添加应力场的作用,目前已有很多学者对其进行了完善,其对现场的耦合效果也较好。其假设如下。
1)土壤连续均匀,且为各向同性的多孔介质。
2)土壤视为理想的弹塑性体。
3)水分迁移只考虑液态方式进行,不考虑气态等其他方式进行的迁移,且满足达西定律,且将水视为无溶质的纯净水,不考虑盐分的影响。
4)水相变为冰热量的改变只考虑热传导的方式,且满足傅立叶定律。
1.1 温度场模型
根据傅立叶传热公式,我们可以得到:
冻结区:
(1)
考虑到相变的影响,则剧烈相变区:
(2)
未冻区:
(3)
为得到统一的表达式,设:
(4)
则将冻结区、正冻区与未冻区的公式得到统一的表达式:
(5)
(6)
(7)
式中,C为土体的体积比热容,kJ/m·℃;T为土体的温度,℃;Tm为初始冻结温度的绝对值,℃;λ为土体的导热系数,kJ/m·h·℃;L为冰水的相变潜热,kJ/kg;ρw为水的密度,kg/m3;θw和θu分别为土体中水分体积总含量;A和B均为常数,取B=0.5;ω0为初始含水率,%。
1.2 渗流场方程
水分的迁移前文已经说到,主要有两种理论:土水势理论以及水动力学模型,本文采用第一种土水势理论来描述水分的迁移。
根据水分迁移公式得:
(8)
ψ=αPw+G
(9)
式中,ψ为土水势;θω为土壤中水分的体积含量;k为土壤导水率,m/s;Pw为水压力,Pa;α为转换系数;G为重力势。
由Clapeyron方程:
(10)
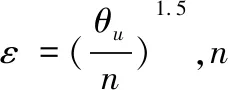
将上面5.16和5.17代入到方程5.18中,得到方程:
(11)
1.3 应力场方程
平衡方程:
[L]{σ}+[G]=0
(12)
几何方程:
{ε}=[L]{u}
(13)
物理方程(本构方程):
{σ}=[D]({ε}-{ε0})
(14)
位移边界条件:
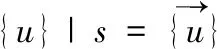
(15)
(16)
应力边界条件:
{σ}[M]=[F]
(17)
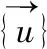
而土体在发生冻胀时,冻胀产生的位移主要由两部分构成:一部分是土体中原来的水分发生原位冻胀产生的位移,另一部分是迁移水分相变为冰产生的冻胀位移。则土壤中的位移变化可以由下式表示:
εv=εvf+εvT
(18)
εvf=0.09(θ0-θu)+1.09θ-n
(19)
式中,εvf为冰水相变产生的体积变形量;εvT为温度变化产生的体积变形量;θ0为初始体积含水量;θu为土壤未冻水的体积含量;θ为迁移来的体积含水量;n为土体孔隙率。
2 模拟工况
根据上海某工程联络通道建设,已知联络通道的右行线隧道中心标高为-7.50 m,所处位置地面标高约为+3.50 m,地层主要为①填土、②1粉质黏土、②2粉质黏土夹粘质粉土、②3砂质粉土、③1淤泥质粉质黏土、③2砂质粉土、④淤泥质黏土、⑤1黏土、⑦1砂质粉土、⑦2-1粉砂、⑦2-2粉砂。
2.1 几何模型
数值模拟建模时对实际工况进行合理简化,能够在保证结果精度的前提下大大提高运算效率。因此,本文建模时从以下几个方面对原型进行了简化。
1)考虑到对称关系,和现场监测点布设,将模型简化为二维模型计算。
2)为了方便计算,将①填土、②1粉质黏土、②2粉质黏土夹粘质粉土合并为粉质黏土层,厚度为3.0 m;砂质粉土层不变,厚度为2.2 m;淤泥质粉质黏土层简化为粉质黏土层,厚度为1.7 m;砂质粉土、淤泥质黏土层不变,厚度分别为 1.5、10 m;最后不考虑第⑦土层,将⑤1黏土层概化为粉质黏土层。这样就得到了土层概化为三种土(粉质黏土、砂质粉土、淤泥质黏土),共6层。
3)地下水位位于地表,即地表以下土体均处于饱和状态。
4)冻结管不考虑倾斜的因素,联络通道选取开挖时的尺寸大小,将现场监测截面处冻结管的位置应用到本模型中。
计算参数如表1~4所示。

表1 土体的导热系数与比热

表2 不同土体的导水率

表3 各土层弹性模量及泊松比随温度变化取值

表4 不同土体的含水量
根据现场实际工况,采用先将地层进行初始固结,得到初始地应力;之后对冻结管设定温度,使其在-30 ℃的条件下对地层进行冻结;之后对地层进行开挖,同时维持冻结的进行;最后一步去除冻结条件,让土层进行自然解冻。由此得到冻结法施工全过程中的温度场和位移场的变化。
2.2 冻结工况
从冻结到开挖再到解冻过程中,主要变化的部分有两个,另一个是联络通道土体的开挖,另一个是冻结管温度设定从-30 ℃到与周围土体相同温度。其主要是在不同时间点发生上述变化。故对于时间的选取,选取与实际工地的相同的时间顺序,即:冻结48天,在第37天开挖,开挖完后继续保持冻结到第48天,之后进行解冻,整个数值模拟进行120天。这部分计算为瞬态计算。
温度场的添加选用COMSOL自带的固体传热模型,将联络通道所在域在48天前导热系数与比热容选取为正常土体,而在37天后导热系数与比热容选用空气。冻结管的温度初始值设定为25 ℃,并将在1 h内迅速降至-30 ℃,之后维持负温到第48天,48天之后冻结管温度设定为与普通土体温度相同;水分场选用COMSOL中的PDE方程来实现,且不受联络通道开挖与冻结管温度的变化的影响;位移场选用COMSOL自带的固体力学模型,同时也是受联络通道开挖与冻结管温度变化两方面的影响,在第37天的时候联络通道部分所在域将不参与力学计算,同时考虑到开挖支护过程中,支护所需时间为3天,按最危险工况来考虑,第40天之后开挖土体后的边界才设置为刚体,在第48天之后进行解冻计算。
3 土体温变化规律
3.1 土体温度变化规律
如图1所示为冻结法施工从冻结到开挖再到解冻全过程,土层温度场的变化情况。
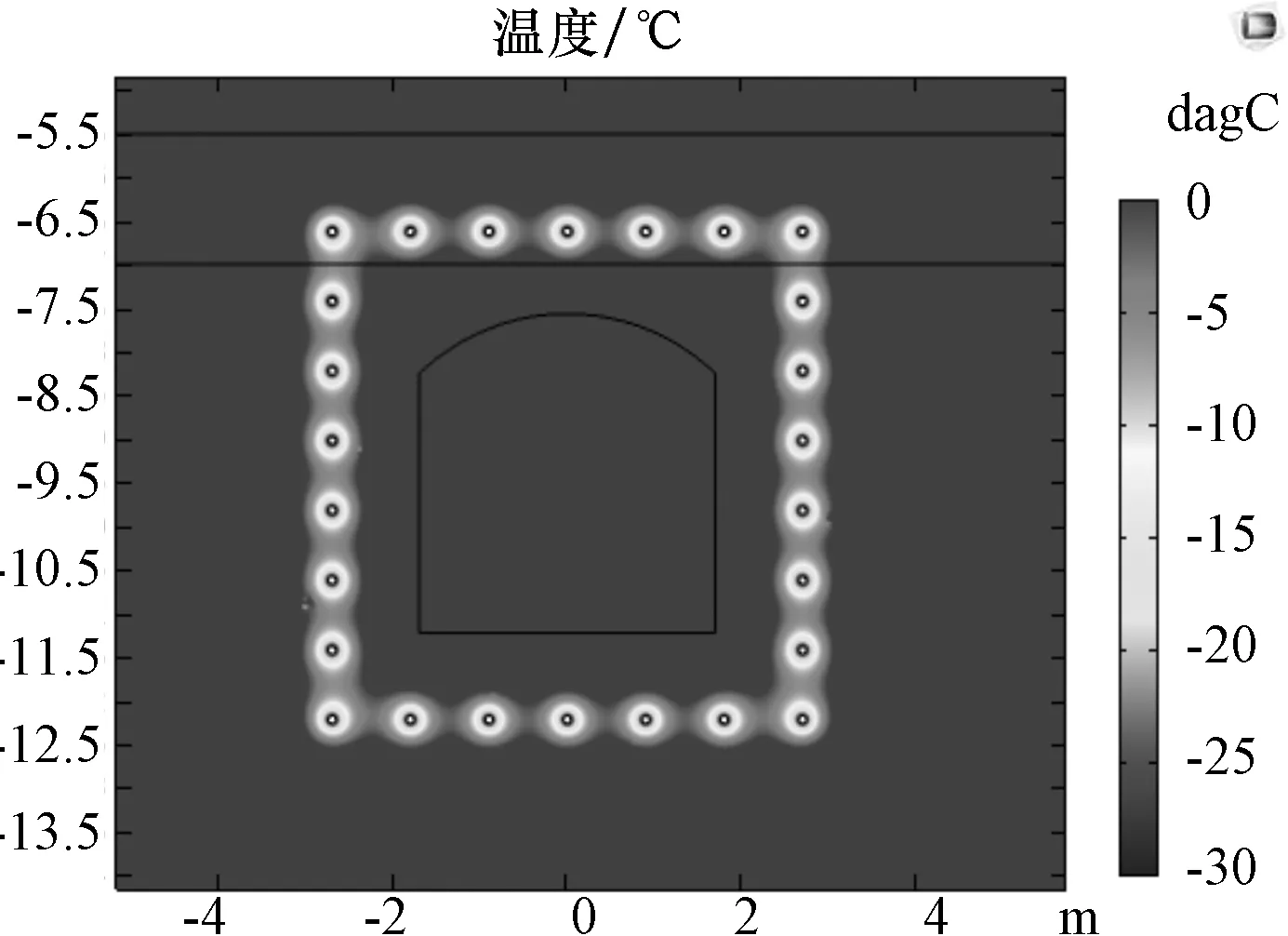
(a)冻结15天温度场
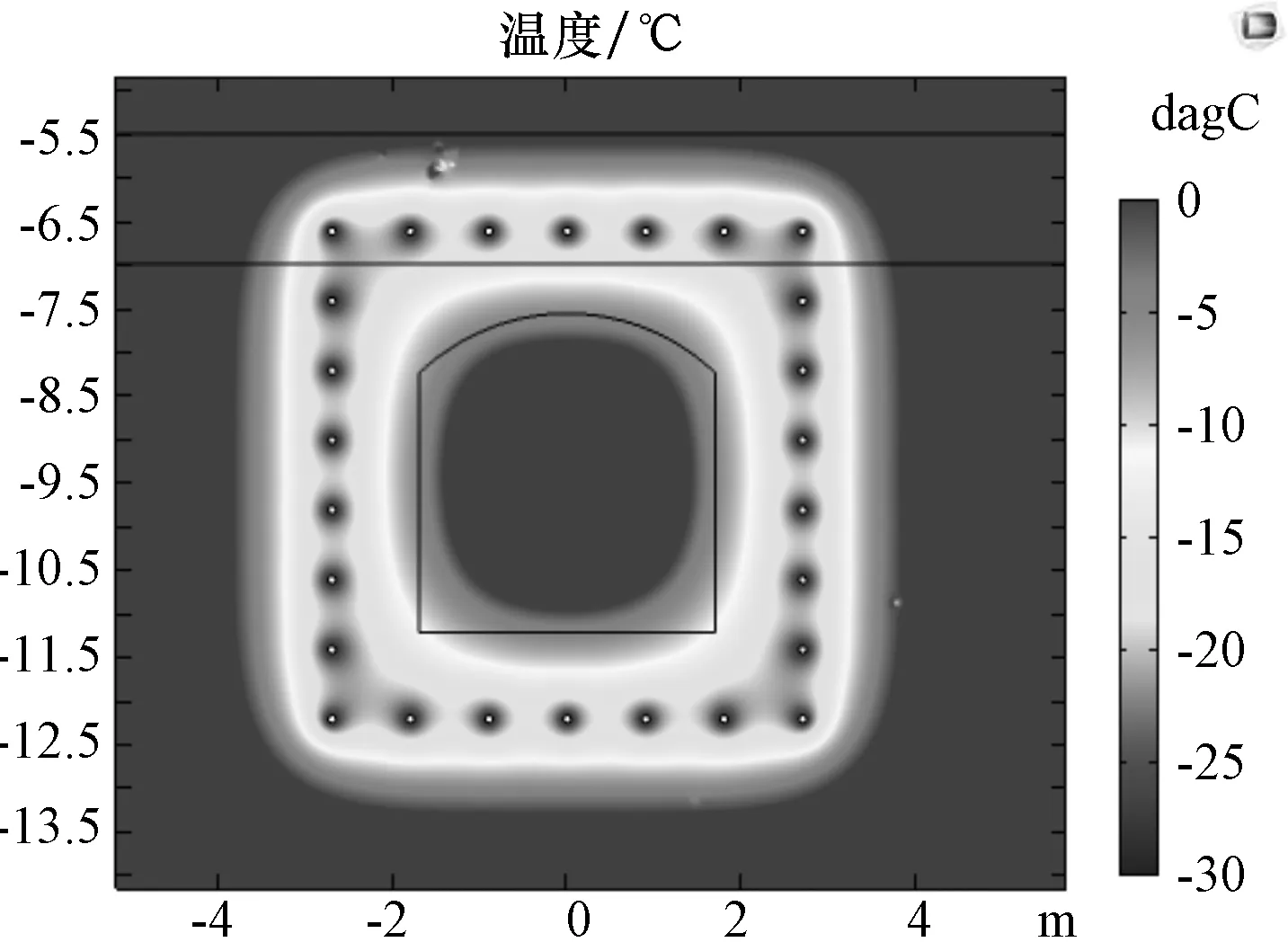
(b)冻结35天温度场

(c)解冻30天后温度场
可以看出,冻结管的冷温不断与周围土体发生热交换,使得周围土体的温度不断降低。在冻结初期,温度基本以冻结管为圆心呈同心圆分布,随着冻结的进行,冻结圈逐渐扩大并相交,由于水平排布的冻结管间距为0.9 m,而纵向排布的冻结管间距为0.8 m,故水平方向上冻结先完成交圈,后是竖直方向上,最终在22天左右形成连续规则的冻土帷幕。为了达到开挖的条件,则又继续进行冻结。冻结壁厚度的设计要求一般为1.5 m左右,经过37天冻结后,经过测量,侧壁厚度已经达到了1.5 m,满足开挖条件。开挖时,将联络通道处土体设置为空气,冻结壁大部分温度保持不变,只是开挖的边缘处温度下降速度变慢。最后是冻结温度场的解冻,在解冻的过程中由于没有冻结管负温的影响,且由于土体温度的均一性,使得温度场呈现同心圆的特点。
在解冻期间,由于冻结壁温度为负,而土层温度为25 ℃,导致外部土层温度仍有下降趋势,将出现图中地表温度与冻结壁外侧温度一致的情况。
3.2 土体位移变化规律
如图2~3所示为冻结法施工冻结到开挖前的过程中,土层位移场的变化情况。可以发现在竖直方向上,上排冻结管发生的冻胀量要大于下排冻结管的冻胀量,且呈现出冻结中间位移大于两边位移的变化规律。冻结管由近及远冻胀量则在减小主要是由于近处产生的位移是由于水结成冰相变所致,而远处的位移则是由于下部土体抬升,同时孔隙压缩,导致最终位移量较小。而在水平方向上,发现土体则呈现出向两侧膨胀的趋势,主要是由于两排冻结管中间土体体积小,土体向中间移动不了,只能向两边位移,而中间部分的土体应力则会增大。开挖后竖向和水平位移见图4~5。
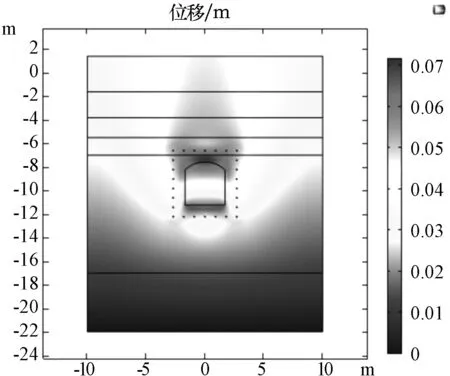
图2 开挖前竖向位移
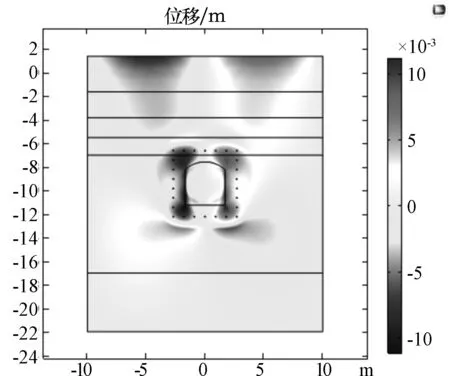
图3 开挖前水平向位移

图4 开挖后竖向位移

图5 开挖后水平向位移
如图4~5所示,在开挖后,由于应力释放,则出现了联络通道上部位移出现负值,即向下位移,而联络通道下部位移为正,即向上位移。在开挖一天后,联络通道上部土体向下位移最大为20 mm,而联络通道下部土体向上位移最大为60 mm,两侧土体向临空面产生位移,位移量为20 mm,说明冻结壁强度达到要求。随着时间的推移,位移量都会迅速增大,因此必须对其进行支护,防止其出现更大的位移变形。
4 结 论
1)利用COMSOL对联络通道冻结法施工全过程进行模拟,发现冻结时温度以冻结管为圆心呈同心圆分布,随着冻结的不断进行,冻结将交圈并不断扩大范围,最终形成连续规则的冻土帷幕,在开挖时将联络通道处土体设置为空气,冻结壁大部分温度保持不变,只是开挖的边缘处温度下降速度变慢。最后是冻结温度场的解冻,在解冻的过程中由于没有冻结管负温的影响,且由于土体温度的均一性,使得温度场呈现同心圆的特点。同时发现空气温度对地层的影响深度为3 m,在解冻后期将影响到冻结壁的解冻。
2)对位移场的影响体现在,竖直方向上,上排冻结管发生的冻胀量要大于下排冻结管的冻胀量,且呈现出冻结中间位移大于两边位移的变化规律。冻结管由近及远冻胀量则在减小主要是由于近处产生的位移是由于水结成冰相变所致,而远处的位移则是由于下部土体抬升,同时孔隙压缩,导致最终位移量较小。而在水平方向上,发现土体则呈现出向两侧膨胀的趋势,主要是由于两排冻结管中间土体体积小,土体向中间移动不了,只能向两边位移,而中间部分的土体应力则会增大。
[ID:009707]

