让孩子的脚步迈起来
杨光有
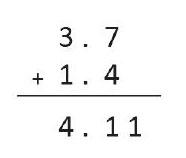
【摘 要】 小学阶段,小数的初步认识安排在三年级,在此之前,学生已经学习了整数,由整数的学习迈向小数的学习,整数学习的一些经验方法一直影响着学生。此外“元、角、分”中的十进制关系可以很好地帮助学生进入小数的内部结构,体会位值。从情境抽象出小数到形式化的理解,学生经历了两次数学化,首先是从现实问题到数学问题的转化,即水平数学化;其次是水平数学化后进行的数学化,是从符号到概念的数学化,即垂直数学化。
【关键词】 数学化;位值;十进关系
一、研究的缘起
每次教小数的内容时,总会遇到这样的问题:
学生在计算小数加法时,总是部分按照整数的形式相加,学完小数的认识,为什么学生会出现这样的问题?具体来说,学生为什么不“跨越”小数点“迈”过去?阻碍学生的“坎”在哪呢?
二、小数的认识都认识什么
(一)数的认识:整数与小数
要想找到这道坎,我们首先看看小数的认识都认识什么。从整体数的认识上看,小数与整数都具有十进制结构,而且学生都经历了数的现实意义的理解,数的读写、新数位的产生、比较大小、运算法则的一系列过程,但同时又有区别,最主要的首先体现在位值制上,数位与位值,其次小数是整数向微观的扩充,由离散走向稠密。
(二)数的认识:小数
整个小学阶段,小数的学习大致分为以下几个年级:三年级,借助“元、角、分”情境初步认识小数;四、五年级,通过更加丰富的实例,拓展学生对小数的认识,进一步抽象出数位,掌握小数运算法则。
(三)认知特点:小数
整个过程可以看出小数学习的认知特点,根据弗赖登塔尔数学化理论:“人们在观察、认识和改造客观世界的过程中,运用数学的思想和方法来分析和研究客观世界的种种现象并加以整理和组织的过程。”简单概括为:数学化的过程是渐进的,其对现实世界场景是逐渐抽象和形式化的。所以数学分为两种,一种是现实问题到数学问题的转化,即水平数学化;一種是水平数学化后进行的数学化,是从符号到概念的数学化,即垂直数学化。
按照上述理论,在数的概念整个建立过程中,可以看出三年级侧重于水平数学化,四年级侧重于垂直数学化。
(四)横向对比
不管是哪种数学化,都让我们直指问题的核心——情境,我们回头再看小数学习的整个过程,为什么都借助于“元、角、分”情境呢?其他版本的教材也是这样的吗?
我们对比一下教材,发现无独有偶,人教版也是借助“元、角、分”情境。这不禁让我们产生一些想法,二年级学生就开始认识“元、角、分”,学生借助它学习小数是不是就没有困难了呢?具体来说,就是学生怎样借助“元、角、分”与小数数位建立联系?“元、角、分”的十进关系,学生又怎样通过位值进入小数的内部结构?前面整数的学习会不会给学生学习小数带来困难?
(五)学生调研
带着这样的想法,我们一起走进学生。
调研题目:你知道3.15元是多少钱吗?可以写一写,画一画。
学生的问题:受整数的影响,学生无形之中把小数分为两部分,每一部分按整数对待,所以完全把整数的位值迁移了过来。
三、要如何认识小数
(一)教学目标
1.结合“文具店”的购物情境,借助元、角、分初步感受小数,关注小数点的作用,体会小数的产生过程,理解小数的实际含义。
2.能将几元几角几分写成以元为单位的小数,感受整数与小数的关系。借小数中各个数字的现实意义,初步体会数字间的十进关系。
3.感受小数在日常生活中的广泛应用,体会数学与日常生活的密切联系。
(二)数学重难点
1.教学重点:在将几元几角几分写成以元为单位的小数中,初步理解小数。
2.教学难点:借助元角分的十进关系,经历由整数迈向小数的全过程,体会小数中的十进位值制。
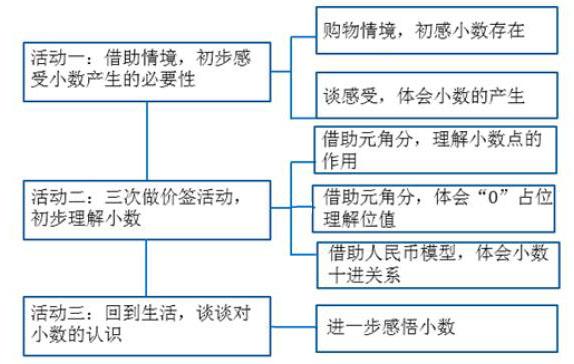
(三)主要活动
1.给钢笔做价签。
出示学生的真问题6.6.6元以及正确的6.66元,学生就真理解了吗?于是追问:你是怎样理解6.66元的?在关注小数点的作用下,学生理解6表示6元,6角,6分,从而由位置“迈”向位值。
2.给铅笔、尺子做价签。
出示学生的作品,在辨析质疑中,提出问题:你们是怎么把价签上的数变成小数的?以元做单位怎么就不能用整数表示了呢?达到明确符号的运用规则,够一元的写在左面,不够一元的写在右面,体会0占位情况,逐步加深对小数的理解。
3.给铅笔盒做价签。
四、教学设计特色
本节课在设计上先是通过符号的关注—小数点,学生从位置迈向了位值,又通过三次做价签,每次按着逻辑上升的顺序,学生由表面迈向内部结构。在整个过程中,学生经历了抽象、操作、发现、交流,放慢了脚步,学生最终从整数迈向了小数。
北师大版教材认识小数时,整数化倾向一直影响着学生;而人教版,先认识分数,后认识小数,分数对小数的学习起到了什么作用?于是我想在下面的研究中,展开对比教学研究。
【参考文献】
[1][荷兰]弗赖登塔尔著,陈昌平,唐瑞芬等编译.作为教育任务的数学[M].上海:上海教育出版社,1995.
[2]张奠宙,宋乃庆.数学教育概论[M].北京:高等教育出版社,2004.

