以立体几何为背景的江苏中高考题的命题趋势

孙宇

【摘 要】 近几年，以立体几何为考查背景的题型层出不穷。在江苏的高考题、中考题、模拟题中大量出现。这一类题目对于学生来说比较新颖，也比较难理解——主要原因在于立体感不强，找不到相应的解答方法。这一类题目，一般情况下都需要在理解题意的基础上，将立体图形转变为平面图形来求解。其中一些高考题目本身也可以利用初中的方法进行求解（相似三角形），而且会更加简单。不仅如此，江苏高考的真题直接影响了中考题型的命题，方法之间也有着异曲同工之妙。对于一些高考真题，进行合理的改编，让初中同学们的思维更加灵活，对于以后的学习有着积极的影响。

【关键词】 立体几何;平面图形;相似三角形

一、利用初中的方法來解答高中题

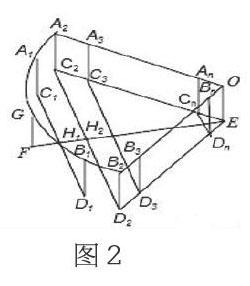
例1：如图1是一个用铁丝围成的篮框，我们来仿制一个类似的柱体形篮框。如图2，它是由一个半径为r、圆心角90°的扇形A2OB2，矩形A2C2EO、B2D2EO及若干个缺一边的矩形状框A1C1D1B1、A2C2D2B2、…、AnBnCnDn，OEFG围成，其中A1、G、B1在上，A2、A3…、An与B2、B3、…Bn分别在半径OA2和OB2上，C2、C3、…、Cn和D2、D3…Dn分别在EC2和ED2上，EF⊥C2D2于H2，C1D1⊥EF于H1，FH1=H1H2=d，C1D1、C2D2、C3D3、CnDn依次等距离平行排放（最后一个矩形状框的边CnDn与点E间的距离应不超过d），A1C1∥A2C2∥A3C3∥…∥AnCn。

（1）求d的值;

（2）CnDn与点E间的距离能否等于d？如果能，求出这样的n的值，如果不能，那么它们之间的距离是多少？

例2：如图3，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm，容器Ⅰ的底面对角线AC的长为10cm，容器Ⅱ的两底面对角线EG，E1G1的长分别为14cm和62cm。分别在容器Ⅰ和容器Ⅱ中注入水，水深均为12cm。现有一根玻璃棒l，其长度为40cm。（容器厚度、玻璃棒粗细均忽略不计）

（1）将l放在容器Ⅰ中，l的一端置于点A处，另一端置于侧棱CC1上，求l没入水中部分的长度;

（2）将l放在容器Ⅱ中，l的一端置于点E处，另一端置于侧棱GG1上，求l没入水中部分的长度。

综合分析：在江苏高考的2016年、2017年连续出现了立体几何的问题。上面的例1是2016年无锡中考的最后一题，例2是2017年的江苏高考真题，这种题型也可在教材上找到它的影子，如苏科版《数学2》（必修）第60页练习第4题。这两道题目的解题方法类似，而且例2作为高考真题可以利用初中的方法进行解答。这两道题目的 基本解题方法均是将立体图形转变为平面图形求解。而立体图转变为平面图的基本方法有两种：一是将图形进行展开（如例3及其变式），另一种就是通过截面图来进行求解——例1作出俯视图、例2作出截面图。对于例1，由于是等腰三角形为背景，只要画出俯视图后，基本上理解清楚题意就可以很快求解出来;对于例2，作出截面图，然后需要利用相似三角形的方法进行求解。读者可以自行做一下这两道例题，相信会有很大收获。

二、江苏高考应用题对中考数学命题的渗透与影响

例3：请你设计一个包装盒，如图4所示，ABCD是边长为60cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得ABCD四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E、F在AB上是被切去的等腰直角三角形斜边的两个端点，设AE=FB=x cm。

（1）若广告商要求包装盒侧面积S（cm2）最大，试问x应取何值？

（2）若广告商要求包装盒容积V（cm3）最大，试问x应取何值？并求出此时包装盒的高与底面边长的比值。

【变式】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD，如图5，再在矩形纸板的四个角上切去边长相等的小正方形，再把它的边沿虚线折起，做成一个无盖的长方体纸盒，底面为矩形EFGH，如图6，设小正方形的边长为x厘米。

（1）当矩形纸板ABCD的一边长为90厘米时，求纸盒侧面积的最大值;

（2）当EH∶EF=7∶2，且侧面积与底面积之比为9∶7时，求x的值。

综合分析：例3及变式的命题背景类似，均是以长方体的展开图为背景，求解相关问题。试题的来源均是这样一道题——苏科版《数学1》（必修1）第二章《函数》的复习参考题：如变式图所示，在一张边长为20cm的正方形铁皮的4个角上，各剪去一个边长是x cm的小正方形，折成一个容积是y cm?的无盖长方体铁盒，试写出用x表示y的函数关系式，并指出它的定义域。题目的解答难度不大，但是却体现了高考命题和中考命题的一种趋势，以立体几何为背景的题型开始显示出威力。立体图形包装盒问题，除了出现在2011年江苏高考题（例3），还出现在2006年无锡中考真题、2010年无锡中考真题中;再从2016年无锡中考模拟题到2017模拟题（如变式2）、2018及2019年模拟题，近几年这类题型层出不穷，大有“翻身”的趋势。

【参考文献】

[1]单遵.普通高中课程标准实验教科书：数学2（必修）[M].南京：江苏教育出版社，2012.

[2]单遵.普通高中课程标准实验教科书：数学1（必修）[M].南京：江苏教育出版社，2012.