计及风险的含电动汽车配电网分布式电源选址定容优化

邓景松 王英民 孙迪飞 晏寒婷 何俸禄

摘 要：考虑电动汽车充电负荷随机性的分布式电源选址定容是目前分布式能源接入时亟待解决的问题。基于电动汽车充电模式、日行驶里程、充电时刻的概率分布模型，利用条件风险价值指标衡量充电负荷接入后配电网电压越限、线路过载及网损升高的风险。提出了计及整体电压水平、线路过负荷及网损等综合风险的配电网DG选址定容优化模型。提出利用纵横交叉算法对优化目标进行求解，最后利用IEEE-33节点系统进行算例仿真，论证了本文所提优化方法的有效性。

关键词：电动汽车;分布式电源;配电网;风险;优化

Abstract：With the popularization of electric vehicles， optimal sizing and placement of DG， the randomness of electric vehicle charging load becomes an urgent problem to be solved. Based on the probability distribution model of electric vehicle charging mode， daily driving mileage and charging time， the conditional risk value index is used to measure the risk of voltage limit violation， distribution line overload and network power loss after charging load are connected to the distribution network. A DG optimal sizing and placement model is proposed under the consideration of comprehensive risks such as voltage level， line overload and network power loss of distribution network. It is solved by the crisscross optimization algorithm. Finally， the IEEE-33 node system is used as the simulation scenario to prove the effectiveness of the article optimization method.

Key words：electrical vechicles;distributed generation;distribution network;risk;optimization

0 引言

目前，我国电动汽车产销保持快速增长，随之而来的则是电动汽车的充电随机性增加了电网安全风险的不确定因素[1-4]。另一方面，分布式电源（DG-Distributed Generation）的接入从电源角度进一步增加了配网运行的随机性。 1）大量充电负荷可能在峰值负荷时段集中接入，增加的负荷需求可能加重电力系统的负担，可能会导致局部电网过负荷;2）充电桩等基础设施的建设将改变配电网网络拓扑结构、增加网络节点、增加线路改造困难和电网损耗等，给电网规划运行带来一系列负面影响和困难。

本文结合电动汽车充电负荷特性建模，基于CVar风险评估理论[5-6]，考虑分布式电源及电动汽车接入后配电网的电压越限及线路过载风险，提出基于一种基于纵横交叉算法（Criss-Cross Optimization）的配电网分布式电源的选址定容优化模型和算法，并利用算例论证了其有效性。

1 电动汽车充电负荷特性建模

根据研究表明，电动汽车的日行驶里程d的概率密度函数近似服从对数正态分布[7-9]，如式（1）所示。

2 分布式电源选址定容优化策略

对于含DG和电动汽车的大型配电网可能出现的风险包括以下两种情况：一是由于系统元件故障引起的电网运行状态的改变，二是因运行条件变化而产生的风险。对于第一种可能发生的情况，影响最大的因素是系统元件的故障率，可通过选用低故障率的元件来提高系统供电可靠性，降低元件的故障概率，以降低风险。对于第二种可能发生的情况，即运行条件变化，包括电动汽车充电无序性，分布式电源出力的不确定性，负荷波动性等，其影响因素非常复杂。其中，电动汽车充电和负荷波动方面与人们的生活习惯相关，因此通过控制其不确定性来降低风险是难以实现的，对于DG则可通过装设控制装置实现对其出力的控制，从而降低其出力不确定性造成的风险。

综上所述，本文以过电压、线路功率两个方面建立目标函数控制DG的出力，以降低系统的风险水平。

2.1 DG控制策略

分布式电源由于能源来源具有出力不确定性的特点，本文通过配套相应大规模的高效储能装置，使得DG出力在一段时间内可视为恒定可控[10]，实现对DG的优化控制。

2.2 电压风险控制策略

对电压风险控制的原則为：将所有节点可能取得的最大可能电压值和最低可能电压值均限制在一定范围内，以尽量降低电压风险。

节点电压可在求解CVaR模型后通过潮流计算获得，设电压CVaR模型的损失函数，如式（3）所示。

2.3 线路过负荷风险控制策略

对含DG和电动汽车的配电网线路过负荷的风险控制原则：降低线路负载率使得其不大于线路的的最大允许传输，即可降低线路过负荷风险。

线路电流可在求解CVaR模型的过程通过潮流计算获得，设其CVaR模型的损失函数，如式（6）所示。

3 含分布式电源和电动汽车的配电网风险控制模型

综合考虑对含DG和电动汽车配电网的电压、线路过负荷的风险优化控制策略，通过改变DG出力对运行风险进行控制和优化，具体模型如下：

4 基于纵横交叉算法的求解算法

为求解含DG和电动汽车配电网的风险控制优化的问题，常用的数学优化方法在求取最优解的过程中存在陷入局部最优和时间收敛较慢的问题。本文采用的是纵横交叉算法（Crisscross optimization algorithm，CSO）的算法[11-12]求上述的风险控制模型。CSO是一种基于种群的搜索算法，其搜索机制由横向交叉和纵向交叉两种方式相互配合，可提高全局的收敛速度和避免陷入局部最优。在迭代过程中每一代这两种行为将交替进行，每次交叉后得出的解称为中庸解（MShc，MSvc）。通过引入竞争算子，使得两种交叉机制有机地结合起来：把交叉后产生的子代进入竞争算子，与其父代进行竞争，保留比父代更优秀的粒子进入下次迭代，最后得出的解称为占优解（DSsc，DSvc）。具体算法流程如下：

（1） 获取父代种群X（第一代为初始化种群，其它代均为纵向交叉产生的占优解矩阵DSvc）;

（2） 对父代种群X中所有个体粒子不重复随机配对，随机生成1到M个随机数，取出相邻两个数作为父代配对粒子的序号i，j;

（3） 父代粒子X（i）和X（j）随机选取第d维进行横向交叉，则它们的子代繁殖采用，如式（11）所示。

（5） 参照（2）中得到配对随机数，执行纵向交叉操作， 式中r在[0，1]之间随机取值，如式（12）所示。

（6） 计算父代种群X中每个粒子的适应度并比较，取得全局最优解gbest，当达到最大迭代次数或迭代多代最优解无变化则终止。

流程图如图1所示。

5 算例分析

5.1 含DG的配电网选址算例分析

以IEEE-33节点系统为分析案例，假设系统接入一台风机与接入一台光伏阵列，其容量分别为1 MW和0.5 MW。此外目标函数中电压、线路过负荷和网损的权重系分别设定为0.4，0.4和0.2。通过计算得到24小时内所有的接入组合，搜索不同组合的24小时综合风险值，其值最小组合的维数就是所求的最佳接入位置。结果如表1所示。

根据计算结果，可知系统综合风险最小的接入方式下风险为0.217 9和综合风险最大的接入方式下风险为0.424 1。不同的接入方式对系统风险水平影响甚大。在不确定性的环境下，对DG进行选址可以较显著提高规划的安全性和经济性。下面通过不同的接入方式间对比说明其影响程度。

设定tsk=14：00，将本文接入方式（简称方式1）、风险最小（简称方式2）和风险最大的接入方式（简称方式3）的电压风险进行对比，结果如图2所示。

对于风险最小和风险最大的接入方式下风险差值比较，后者大于前者24.54%;从图2中明显可见后者从节点9至节点18，其电压风险大于前者。对于风险最小和本文的接入方式下的风险差值比较，后者大于前者5.52%;从图2中明显可见后者从节点27至节点33，其电压风险大于前者。

以tsk=14为例，计算整理的网络损耗风险，具体数值如表2所示。

通过计算得到24小时内所有的接入组合的综合风险值枚举得到最小的风险值，获取其组合的维数。根据维数确定光伏阵列和风机的接入位置，使得系统在不确定性环境下获得最佳的风险水平。该方法对大型的分布式电源并网的规划研究有着重要的意义，如图3所示。

5.2 含DG与电动汽车的配电网选址定容算例分析

5.2.1 IEEE-33节点系统算例分析1

本节以IEEE-33节点系统为分析案例，并网情况如下所示：电动汽车渗透率为20%，其负荷平均分布在节点5、节点10和节点25;为了实现对DG出力的优化控制，本文对光伏阵列的并网节点同时配置了一套储能系统。风机、光伏阵列和储能电池的容量分别为1 MW、0.5 MW和0.5 MW。假设系统接入一台风机与接入一台光伏阵列和储能系统。采用上节提出的枚举方法，获取最佳的DG的接入位置。结果如表3所示。

按照表3中的DG接入方案接入光伏阵列和储能电池、风机;假设3种DG出力区间分别为[0.2 MW，1 MW]、[-0.5 MW，0.5 MW]和[0，0.5 MW]。此外计算综合风险的目标函数中电压、线路过负荷和网损的权重系分别设定为0.4、0.4和0.2。算法的种群规模为30，最大迭代次数为100次，横向交叉率为0.9和纵向交叉为0.7。tsk=21：00和tsk=7：00为系统的峰谷值，以这两个时间段作为输入最具代表意义。具体优化结果如表4所示。

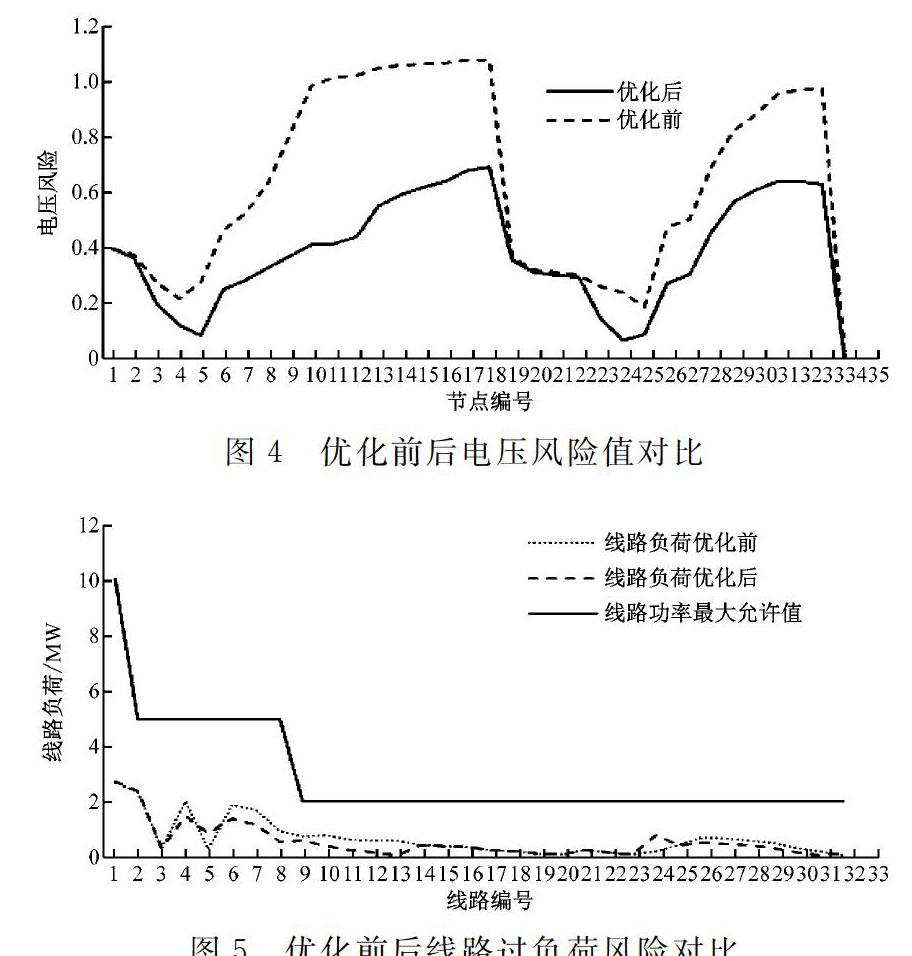
从表4可以直观地看到tsk=21：00时段，由于光伏电源不出力和负荷需求处于波峰而导致风机和储能电池出力值达到最高限制值，系统整体的风险值0.110 6比tsk=7：00时间的整体风险值高0.074 5，前者是后者的三倍。下面选择tsk=7：00时段对比优化前后电压、线路功率和网损数据，如图4、图5所示。

从图4和图5中可以明显看出优化后系统各个节点的电压风险明显的降低，整体电压风险水平相对优化前降低了39.3%。而由于实际的线路功率相比线路最大功率允许值相差较远，故线路过负荷整体风险值优化前后均为0，但是优化前大部分线路CVaR风险值高于优化后。

5.2.2 IEEE-33节点系统算例分析2

同样以IEEE-33节点系统为分析案例，并网情况如下所示：電动汽车渗透率为20%，其负荷平均分布在节点5、节点10和节点25;DG接入情况与上节相同。随机生成一组DG的接入组合，在此基础上通过CSO求解优化控制模型得到DG的最佳出力。风机的出力区间为[0.2 MW，1 MW]，储能系统的出力区间为[-0.5 MW，0.5 MW]。此外目标函数中电压、线路过负荷和网损的权重系分别设定为0.4、0.4和0.2。算法的种群规模为30，最大迭代次数为100次，横向交叉率为0.9和纵向交叉为0.7。tsk=21：00和tsk=7：00大概是系统的峰谷值，以这两个时间段作为输入最具代表意义。具体优化结果如表5所示。

从表5中两者的对比结果可见，两种不同的接入组合使得在DG最佳出力的情况下整体的风险相差很大。tsk=7：00时段两种不同接入方式下电压、线路功率，如图6、图7所示。

由图6和图7中可以明显看出两种接入方式优化结果的对比情况，采用（18，30）的接入方案，系统部分节点的电压风险和线路负荷明显比（23，18）接入方案要小。综上所述，本文考虑通过计算所有组合的综合风险值并对其求和，枚举得到最佳的接入组合，对降低系统的整体风险有一定的意义。

6 总结

文章在对电动汽车充电模式、日行驶里程概率分布和充电时刻概率分布模型的基础上，研究了考虑整体电压风险、线路过负荷风险和网损风险的综合风险的配电网DG选址定容优化问题。利用IEEE-33节点系统进行仿真分析，并利用CSO算法求解优化模型，证明了所提出的综合风险目标函数的有效性，仿真结果表明，优化方法的优化结果有助于提高系统运行的安全性和经济性，且对系统负荷的波动性有较强的适应性。

参考文献

[1] 李立理，张义斌，周原冰，等. 我國发展电动汽车充电基础设施若干问题分析[J]. 能源技术经济，2011（1）：6-10.

[2] 刘焕. 电动汽车充电站建设项目群风险研究[D].重庆：重庆大学，2009.

[3] 厉志辉. 电动汽车充电站对电网影响[D]. 济南：山东大学，2013.

[4] 徐虹，贺鹏，艾欣.电动汽车充电功率需求分析模型研究综述[J]. 现代电力，2012，29（3）：51-55.

[5] CIGRE Task Force 38 03.12. Power System Security Assessment：A Position Paper[R]. Electra， 1997 （175）：49-77.

[6] McCalley J D， Vittal V， Abi-Samra N. An overview of risk based security assessment[C]//Power Engineering Society Summer Meeting， 1999. IEEE. IEEE， 1999， 1：173-178.

[7] 田立亭，史双龙，贾卓. 电动汽车充电功率需求的统计学建模方法[J]. 电网技术，2010（11）：126-130.

[8] Taylor M J，Alexander A.Evaluation of the impact of plug-in electric vehicle loading on distribution system operations[C]//IEEE Power &Energy Society General Meeting，Calgary，Canada，2009：1-6.

[9] Doucet A， Singh S S. Particle methods for change detection， system identification， and control[J]. Proceedings of the IEEE， 2004， 92（3）：423-438.

[10] Schilling M T， Do Coutto Filho M B， da Silva A M L， et al. An integrated approach to power system reliability assessment[J]. International Journal of Electrical Power & Energy Systems， 1995， 17（6）：381-390.

[11] 孟安波，卢海明，李海亮，等. 纵横交叉算法优化FCM在电力客户分类中的应用[J]. 电力系统保护与控制，2015（20）：150-154.

[12] MENG A， CHEN Y， YIN H， et al. Crisscross optimization algorithm and its application[J]. Knowledge-Based Systems， 2014（67）：218-229.

（收稿日期：2019.09.20）