基于LSTM的评论文本情感分析方法研究
李井辉 孙丽娜 李晶


摘 要:长短时记忆神经网络(long short-term memory,LSTM)是一种特殊形式的循环神经网络。是为了解决基于长文本序列的模型训练过程中的梯度消失和梯度爆炸等问题而提出的。相对于传统的循环神经网络,LSTM在长序列上有更好的表现。LSTM是一种包含重复神经网络模块的链式形式,在该链式模式中,重复的模块有着不同的结构,其中包括输入门、遗忘门和输出门。介绍了LSTM的工作原理并将其应用到文本情感分析领域,然后,结合Word2Vec词嵌入技术在大规模文本情感分析数据集上进行实验,将LSTM与基于卷积神经网络(CNN)的方法进行实验对比,最终发现LSTM相较于传统的CNN方法在文本情感分类的准确率方面取得了更好的表现。
关键词:文本情感分析;LSTM长短时记忆神经网络;卷积神经网络;词嵌入技术
Abstract:Long short-term memory (LSTM) is a special form of recurrent neural network. It was proposed to solve the problems of gradient vanish and gradient explosion in the training of long text sequences. Compared with the traditional recurrent neural network, it has better performance on long sequences. LSTM is a chained form that contains repetitive neural network modules which have different structures including input gates, forgetting gates, and output gates. This paper introduces the main theory of LSTM and applies it to the field of text sentiment analysis. Then, we combine the word embedding technique Word2Vec and conduct experiments on large-scale text sentiment analysis dataset, compare the LSTM with convolutional neural network (CNN). We finally find that LSTM performs better in terms of the accuracy on the task of text sentiment classification compared with the traditional CNN method.
Key words:text sentiment analysis;long-term memory neural network;convolutional neural network;word embedding technology
0 引言
情感分析是自然語言处理NLP领域最受欢迎的应用之一[1],由于其应用的广泛性及重要性,近年来,越来越多的研究者专注于分析从公司调查到电影评论等各种数据集的情感。情感分析的关键是分析一组文本以理解其所表达的观点。通常,我们用正值或负值量化这种情绪,称为情感极性。从极性分数的符号来看,总体情绪通常被推断为正面及负面[2-3]。本文主要是将LSTM[4]应用于情感分析领域,结合Word2Vec词嵌入技术[5]来进行实验,并与传统的基于CNN的情感分类方法[6]进行对比。
1 相关研究现状
1.1 情感分析
文本情感分析致力于将单词、句子和文档映射到一组相对应的情感类别上,继而得到一个可用于划分情感状态的心理学模型。近十年来,深度神经网络取得了极大的进展,各个主流领域,包括图像分类、机器翻译、自然语言处理、语音识别等,均依赖于深度学习技术提供的高层语义特征及分类方法。其中,卷积神经网络(CNN)和和以长短期记忆网络(LSTM)为代表的循环神经网络(RNN)由于强大的建模能力而被广泛使用。
1.2 Word2vec词嵌入技术
自然语言是一套用来表达语句含义的复杂系统。在该系统中,词(以及中文中的字)是表达含义的基本单元。顾名思义,词向量是用来表示词的向量,也可以被认为是词的特征向量或表征。把词映射为实数域向量的技术也叫词嵌入技术。
假设词典中不同词的数量(词典大小)为N,每个词可以和从0到N-1的连续整数一一对应。这些与词对应的整数叫作词的索引。假设一个词的索引为i,为了得到该词的独热编码向量表示,我们创建一个全0的长为N的向量,并将其第i位设成1。这样一来,每个词就表示成了一个长度为N的向量,可以直接被神经网络使用。
词嵌入模型的训练目标是找到对预测句子或文档中的周围单词有用的单词表示。更正式地说,给定一系列训练单词w1,w2,w3,…,wT,其目标是最大化以下平均对数概率(度量了单词间的相关性),如式(1)所示。
其中c是训练上下文的大小(可以是中心词wt的函数)。 较大的c带来更多训练示例,因此,可以以训练时间为代价带来更高的准确性。
1.3 长短时记忆LSTM
在90年代中期,德国研究人员Sepp Hochreiter和Juergen Schmidhuber提出了一种带有所谓长短时记忆(LSTMs)的循环神经网络的变体,作为解决消失梯度问题的方法。LSTM[7-8]有助于保留可以通过时间和层反向传播的梯度。通过保持更加稳定的梯度,它们允许循环网络继续学习多个时间步长(超过1 000),从而建立一个通道以在较远的时间步长范围内连接原因和结果。
LSTM包含门控单元中循环网络正常输入输出流之外的信息。信息可以存储在单元中,可以写入单元或从单元读取,就像计算机存储器中的数据一样。单元通过打开和关闭的门来决定存储什么,何时允许读,写或擦除。然而,与计算机上的数字存储不同,这些门是模拟的,通过sigmoid[9]的乘法实现,它们都在从0到1的范围内。由于是模拟的,因此具有可微分性,适用于反向传播。
这些门对它们接收的信号起作用,并且类似于神经网络的节点,它们根据其强度和导入来阻止或传递信息,它们使用它们自己的权重集进行过滤。这些权重,如调整输入和隐藏状态的权重,通过循环网络学习过程进行调整。也就是说,网络模块学习何时允许数据进入、离开或删除,学习反向传播梯度并通过梯度下降方法调整权重的迭代过程。
在分类过程中,以LSTM为代表的循环神经网络有自己的记忆。具体的数学形式,如式(2)所示。
2 实验
2.1 数据集选取
使用斯坦福的大规模电影评论数据集(Stanfords Large Movie Review Dataset,IMDb[1])作为文本情感分析实验的数据集。该数据集从IMDB电影评论网站收集了50 000条评论,每部电影不超过30条评论。在该数据集中,标签为“正面情感”和“负面情感”的评论数量相等,因此随机猜测将产生50%的准确性。 该数据集只保留了高度两极化的评论,负面评价的得分≤4分,总分为10分,正面评价的评分为≥7分。中性评价不包括在数据集中。该数据集分为训练和测试两个集合,分别包含25 000条评论。数据来源:http://www.andrew-maas.net/data/sentiment。
2.2 LSTM网络搭建
对于选取的数据集,我们搭建的LSTM模型结构如下:
第一层,特征提取层,利用word2vec将词语映射成128维向量;
第二层,循环神经网络中的长短时记忆模块。在一条时间序列上,首先将提取到的特征送入输入单元,在这之后,一條数据流从输入单元送到隐含单元,另一条则从隐含单元送到输出单元。这里的隐含单元便是神经网络的记忆单元。对于某一个隐含单元,以xt表示当前第t步的输入,神经网络根据当前输入层的输出和上一步隐含层的输出计算目前单元的激活值:s=f(Uxt+Wst-1)。这里的f为非线性的激活函数,本文选择ReLU。最后,第t步的输出由softmax层计算得出;
3)反向传播。本文利用基于时间步的反向传播技术对网络进行迭代更新。
4)训练完成后,保存模型参数,并使用测试集对模型能力进行评估。测试方法与训练过程类似,将用于测试的评论样本作为输入,过训练好的LSTM一次得到最终的预测标签,与数据集中给定的真实标注(Ground Truth)进行比较得到准确率。
2.3 CNN网络搭建
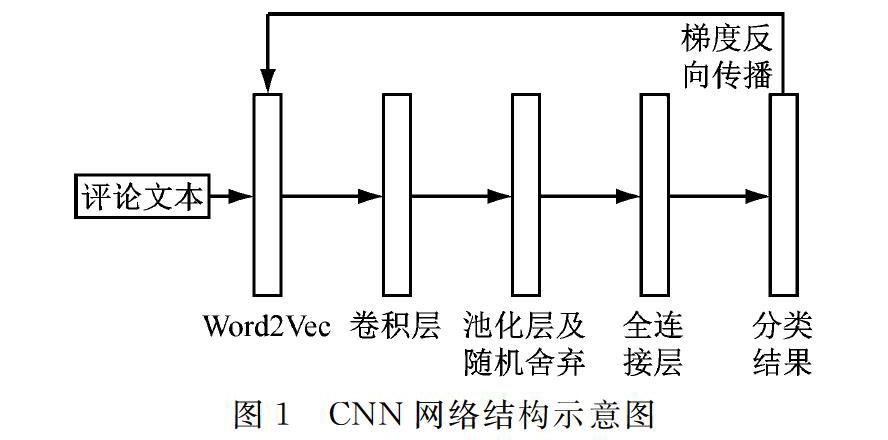
本文设计的CNN模型结构,如图1所示。
第一层,特征提取层,利用word2vec将词语映射成128维向量;
第二层,卷积层,设计了多个尺寸的滤波器可以在每次训练过程中分别划分3、4、5等不同数量的字词;
第三层,池化层,本文采用的是最大池化,该层将所有卷积层的结果映射到了一个一维的特征向量上;
第四层,随机舍弃神经元,即dropout正则化层,这样做可以使神经网络有更好的泛化能力。
最后一层,全连接及softmax层,给出模型预测的结果。
3)使用交叉熵损失作为本文模型的损失函数,通过梯度下降、反向传播等技术迭代更新模型参数。
4)训练完成后,保存模型参数,并使用测试集对模型能力进行评估。测试方法与训练过程类似,将用于测试的评论样本作为输入,过训练好的CNN一次得到最终的预测标签,与数据集中给定的真实标注(Ground Truth)进行比较得到准确率。
3 预测结果与分析
本文按照第2章中所描述的网络搭建方式在大规模电影评论数据集上进行了对比实验。模型参数如下:对于LSTM,我们设置学习率为0.01,设置训练批次大小为64(每次梯度的更新根据随机选取的64张文本进行计算),词向量长度为100,隐藏层单元数为100,隐藏层层数为2;对于CNN,我们设置其学习率为0.01,设置其训练批次大小为64,词向量长度为100,每个层的神经元数量均为100,卷积核大小为3。本文共进行600次迭代(每次迭代均按批次遍历数据集所有文本)。详细实验结果,如表1所示。
表1给出了本文对比实验的结果。其中,分别给出了LSTM和CNN在特定迭代步骤处的训练损失值、训练准确率和测试准确率。可以看出,CNN模型收敛较快但是达到的最高测试准确率远低于LSTM(CNN最高为82.8%,LSTM在600次迭代内最高准确率为86.9%,且仍有可能上升)。对于CNN模型,其训练损失及训练准确率在第5次迭代后便分别达到0.05及97.4%,说明模型已经出现了过拟合的现象,产生了梯度消失且后续训练中模型准确率并未上升。对于LSTM,其训练损失及训练准确率一直保持在正常值,说明LSTM模型有效地解决了梯度消失及过拟合的问题。
综合以上结果可以看出,LSTM模型相比CNN模型更适合文本情感分析任务的处理。
4 总结
本文首先对情感分析研究现状和文本特征提取、基于LSTM的文本情感分类技术做了概述,然后通过实验验证了在大规模电影评论数据集上,LSTM方法相对于传统CNN方法的有效性,证明了长短时记忆模块的加入以及LSTM网络特有的循环处理文本特征的方式在分析文本情感特征问题上的有效性。本文采用控制变量的方式对比两种分类方法,采用相同的word2vec词嵌入技术提取文本特征,保证了实验的公平性。本文对于评论文本情感分析领域的研究,特别是对基于深度神经网络(包括CNN和RNN)的方法的选取,有一定的指导意义。
參考文献
[1] 唐慧丰,谭松波,程学旗.基于监督学习的中文情感分析技术比较研究[J].中文信息学报,2007,21(6):88-95.
[2] Maas A L, Daly R E, Pham P T, et al. Learning word vectors for sentiment analysis[C]// Proceedings of the 49th annual meeting of the association for computational linguistics:Human language technologies. Association for Computational Linguistics (USA. 2017):142-150. (2011, June).
[3] Siegelmann, Hava T, Sontag Eduardo D. On the Computational Power of Neural Nets. ACM. COLT '92:440–449. doi:10.1145/130385.130432.
[4] Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural computation, 1997,9(8):1735-1780.
[5] Mikolov Tomas, Kai Chen, Greg Coeeado, et al. Efficient Estimation of Word Representations in Vector Space[J]. arXiv, 2013:1301.3781 [cs.CL].
[6] Kim Y. Convolutional neural networks for sentence classification. arXiv, 2014:1408.5882.
[7] Klaus Greff, Rupesh Kumar Srivastava, Jan Koutník, et al. LSTM:A Search Space Odyssey[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 28 (10):2222–2232.
[8] Felix Gers, Jürgen Schmidhuber, Fred Cummins. Learning to Forget:Continual Prediction with LSTM[C]// Proc. ICANN'99. IEE, London, 1999:850–855.
[9] Rafferty J, Shellito P, Hyman N H, et al.. Practice parameters for sigmoid diverticulitis[J]. Diseases of the colon & rectum, 2006,49(7):939-944.
[10] Green P J. Reversible Jump Markov chain Monte Carlo Computation and Bayesian Model Determination[J]. Biometrika, 1995, 82(4):711-732.
[11] Malfliet W, Hereman W. The tanh method:I. Exact solutions of nonlinear evolution and wave equations[J]. Physica Scripta, 1996,54(6):563.
(收稿日期:2019.03.18)

