超高性能混凝土与三维CAE仿真分析在特殊桥梁工程中的运用
王 新,李国鹏,赵卓显
(中国电建集团北京勘测设计研究院有限公司,北京 100024)
0 前 言
随着我国经济快速发展,对基础设施建设也提出了更高的要求。一方面,城市对桥梁提出了更多的功能要求;另一方面,城市桥梁除提供交通功能外,美观性也愈发被重视。这便促使一些特殊桥梁应运而生,例如,开启式桥梁[1]既满足航运的水位要求,又因常采用轻质美观的钢结构、开启或闭合的过程更易吸引人们的关注等原因,而具有很好的景观性[2]。
钢-普通混凝土桥面板是通过抗剪连接件将钢梁和混凝土板组合而成,充分利用混凝土高强的抗压性和钢材良好的抗拉性,具有结构受力合理的特点,在特殊桥梁工程中广泛应用。但同时也存在自重大、负弯矩区域混凝土易开裂等缺陷,影响了结构的耐久性和经济性[3]。
随着科技的快速发展,混凝土强度越来越高,超高性能混凝土(UHPC) 应运而生[4]。与普通混凝土相比,UHPC以细砂为骨料,掺入大量硅灰等矿物掺合料、高效减水剂和微细钢纤维,其抗压强度可达到200 MPa,抗弯拉强度可达到20 MPa。
为改变上述钢-普通混凝土组合梁的不足,可采用超高性能混凝土(UHPC)替代普通混凝土,形成钢-UHPC组合桥面板。由于UHPC优良的材料性能非常适合应用于桥梁工程中,目前全世界已建成的UHPC桥梁有200多座[5],但应用钢-UHPC组合结构的却很少。对于钢-UHPC组合结构的理论研究,国内已经开展了一些[6-7]。根据这些研究结果可以得到一个结论:采用UHPC板替代传统钢-混凝土组合梁中的普通混凝土,形成钢-UHPC组合梁,在桥梁工程中具有良好的应用前景[8]。
为深入探究钢-UHPC组合桥面板的受力特性,本文结合工程实例研究不同混凝土厚度、约束方式与加劲肋形式对其的影响,得出的相关结果可为其他工程提供参考。
1 桥面板精细化模型与边界约束对桥面板的影响
1.1 桥面板设计方案
本文以通州某开启桥为研究对象,因桥台需设置机械转动装置、动力系统及定期检修通道等,0号桥台设计为较大空间的箱室结构。为防护机械装置、保障结构安全性及桥梁美观性,本桥需在桥台处布置一块较大跨径的钢-UHPC组合桥面板,同时也作为箱室桥台的顶板,详见图1。该桥面板具有以下特点:
(1)受机械装置影响,板的几何形式较为复杂。
(2)转轴侧板边不受约束,其余三侧均约束在桥台处。
(3)板顶高程需满足桥面高程要求,板底不得侵占配重空间,因此组合板厚度受到限制。具体设计方案为UHPC混凝土、Q420钢板和纵横方向加劲肋三者的组合结构。桥梁开启状态下,该桥面板仅有自重和温度荷载,荷载标准组合=1.0×自重+1.0×温度荷载(整体降温20 ℃)。桥面板平面设计示意见图2,桥面板立面设计及材料剖面示意见图3。

(a)平面 (b)立面
1.2 精细化设计模型与固定约束对比模型
约束方式对于桥面板的受力响应至关重要。设计方案采用搭接支承的方式,即在重力方向限制节点向下移动,不限制节点向上移动。为准确模拟搭接支承,模型在搭接处增加仅能承压、不承拉的大刚度虚拟接触杆单元。所以,依据设计方案,采用上述模拟方法,建立了精细化模型。

图2 桥面板平面设计(单位:mm)

图3 桥面板立面设计及材料剖面示意(单位:mm)
此外,钢结构施工中常常还采用螺栓、焊接等固定约束的方式。因此,在不改变其他任何参数的前提下,本节通过建立固定约束的对比模型,探究约束方式对于桥面板受力特性的影响。模型参数详见表1。

表1 模型对比
1.3 结果对比分析
设计模型与对比模型的主要计算结果如图4~11所示。
通过挠度云图对比可知,设计模型混凝土挠度最大为2.3 cm,而对比模型最大挠度为1.1 cm。应力云图对比可知,设计模型的各材料应力分布变化平缓,而对比模型在靠近约束区域内存在明显的应力集中现象,混凝土与钢材应力均很大。显然,相比固定约束,搭接支承的结构产生较大挠度,但能够有效避免支撑范围内的应力集中现象,使桥面板应力分布变化更加平缓。
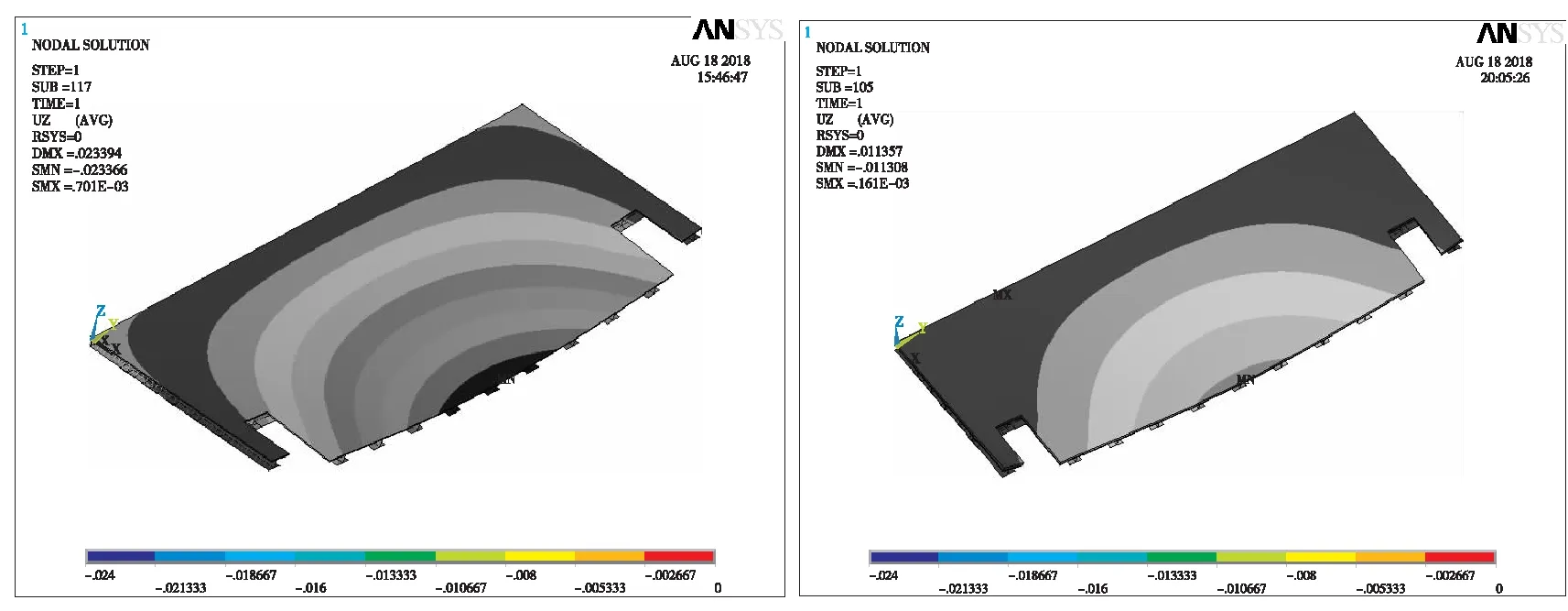
图4 设计模型混凝土挠度云图 图5 对比模型混凝土挠度云图
图6 设计模型混凝土主压应力云图 图7 对比模型混凝土主压应力云图

图8 设计模型桥面钢板米塞斯应力云图 图9 对比模型桥面钢板米塞斯应力云图
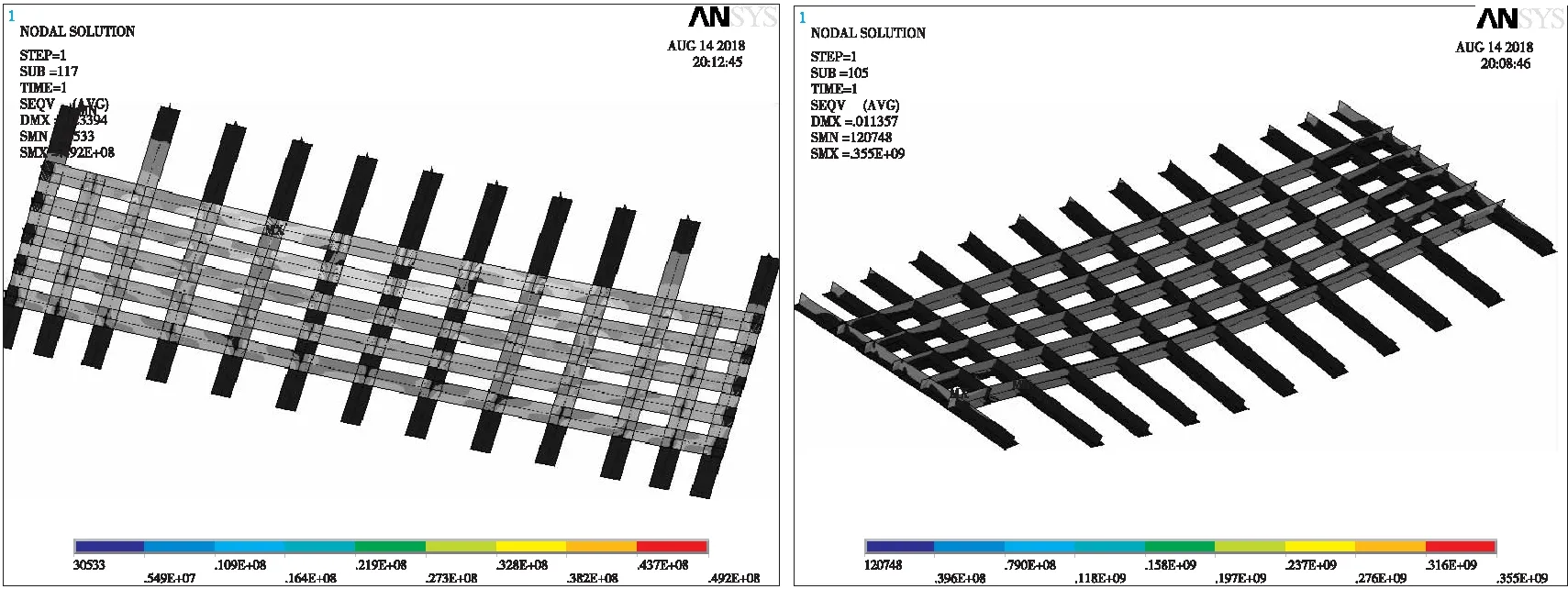
图10 设计模型T肋米塞斯应力云图 图11 对比模型T肋米塞斯应力云图
2 混凝土厚度对桥面板的影响
2.1 不同参数的对比模型
受桥面高程和配重构件的影响,本桥面板总厚度不能超过250 mm。所以在总厚度不变的前提下,本节通过建立不同厚度混凝土的桥面板模型,探究混凝土厚度对于桥面板力学特性的影响,模型参数详见表2。
2.2 挠度结果对比分析
各模型计算结果的挠度云图如图12所示。
最大挠度出现在悬臂侧,提取各模型悬臂侧的挠度计算结果并形成挠度对比(见图13)。Y轴为挠度计算值,X轴为沿线位置坐标,即未支承侧边上任意点沿边线到最左侧端点的距离。
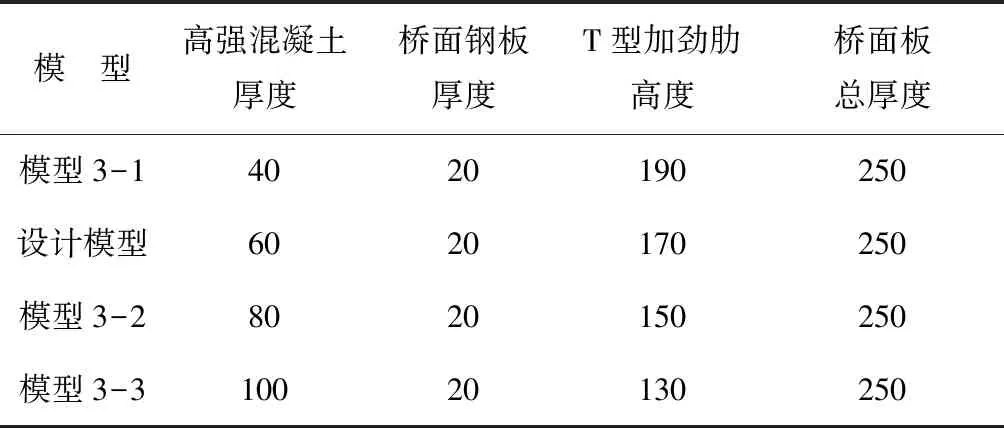
表2 模型参数 mm

图12 各模型挠度云图对比
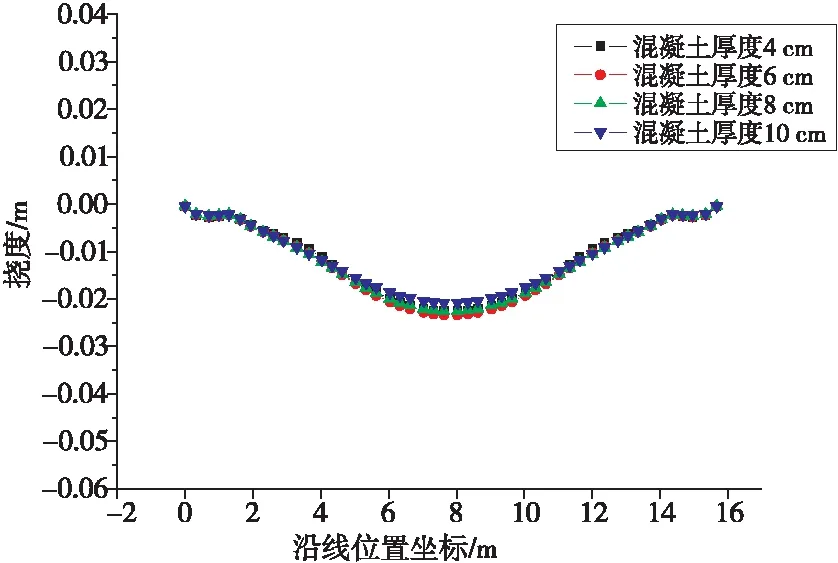
图13 挠度对比
可见,混凝土厚度的变化对于桥面板挠度影响很小。
2.3 混凝土压应力结果对比分析
提取各模型悬臂侧混凝土主压应力计算结果,并形成混凝土主压应力对比图(见图14)。Y轴为应力值,X轴为沿线位置坐标,即悬臂侧边上任意点沿边线到最左侧端点的距离。各模型混凝土主压应力云图如图15所示。
根据结果可知:随着混凝土厚度由4 cm增大到6 cm,跨中区域的混凝土最大压应力由约6 MPa逐渐减少至约3 MPa;混凝土厚度由8 cm增大到10 cm,跨中区域的混凝土最大主压应力由约3 MPa逐渐增大到约7 MPa ;在桥面板几何变化区域内,混凝土出现应力集中现象,且随着混凝土厚度的增大,最大应力也逐渐增大。
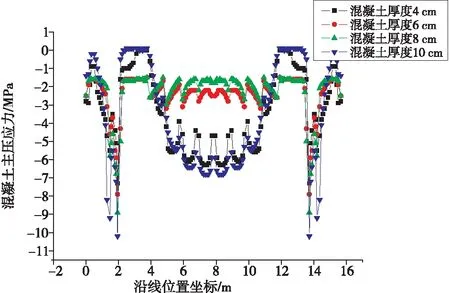
图14 混凝土主压应力对比
2.4 钢材应力结果对比分析
各模型计算结果的钢材米塞斯应力云图如图16所示。
最大应力出现在靠近悬臂侧加劲肋上,提取该加劲肋各位置处米塞斯应力,并形成对比图(见图17)。Y坐标是应力值,X坐标对应节点沿线位置坐标,即加劲肋上任意点沿横桥向到肋端点的距离。
分析可知,随着混凝土厚度由4 cm增大到10 cm,加劲肋的最大应力均出现在两侧几何变化的区域内,基本维持在50 MPa左右。

图15 各模型混凝土主压应力对比云图
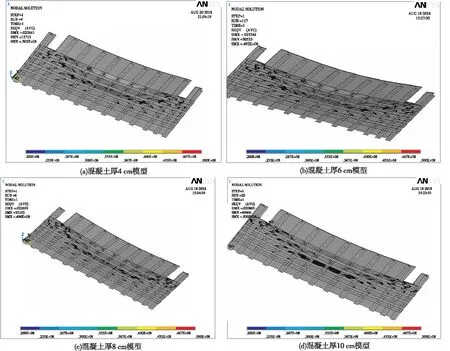
图16 各模型钢材应力对比云图
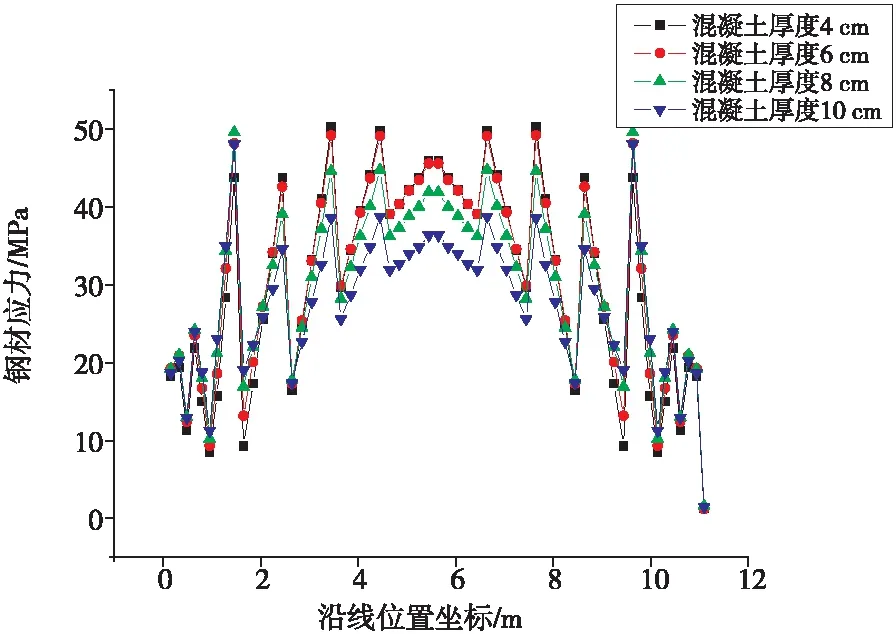
图17 钢材应力对比
2.5 小 结
根据上述分析,得出以下三点结论:
(1)混凝土厚度的变化对桥面板的挠度几乎无影响。
(2)随着混凝土厚度由4 cm增加到10 cm,跨中混凝土压应力先递减后递增。当厚度在6~8 cm范围内时,跨中混凝土压应力最小。
(3)桥面板两侧几何变化区域出现应力集中现象。
3 加劲肋形式对桥面板力学特性的影响
为增加钢结构刚度及避免结构失稳,组合桥面板需要设置加劲肋。加劲肋的形式主要有T型加劲肋与U型加劲肋。工程实践中,受到施工技术、材料工艺、力学特性等因素的影响,钢结构会相应选取适当形式的加劲肋。本节通过设计模型与U型加劲肋模型的对比分析,探究加劲肋形式对于钢-UHPC 组合桥面板力学特性的影响。
3.1 U型加劲肋的对比模型
设计方案采用高度170 mm的T型加劲肋。在设计方案基础上,对比方案将所有轴向为横桥向的T型加劲肋改为U型,且两种方案的高度、厚度及横断面面积保持一致,具体参数如图18~19所示。
3.2 结果对比分析
设计模型与U肋对比模型的计算结果如图20~25所示。
通过挠度云图的对比可知:T肋桥面板最大挠度为2.3 cm,混凝土最大压应力为10.8 MPa,靠近悬臂侧的加劲肋在中间区域内出现了最大米塞斯应力为49.2 MPa。U肋桥面板最大挠度为2.1 cm,混凝土最大压应力为14 MPa,钢材最大米塞斯应力为93.0 MPa,且钢材最大应力均出现在桥面板几何变化区域的外侧加劲肋上。显然,在肋高、肋板厚度与工程量相同的前提下,U肋桥面板挠度要小于T肋桥面板,但T肋更能够减轻桥面板两侧几何变化区域内应力集中的现象。
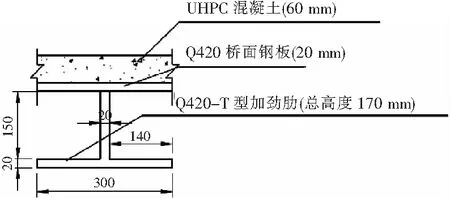
图18 设计方案剖面示意
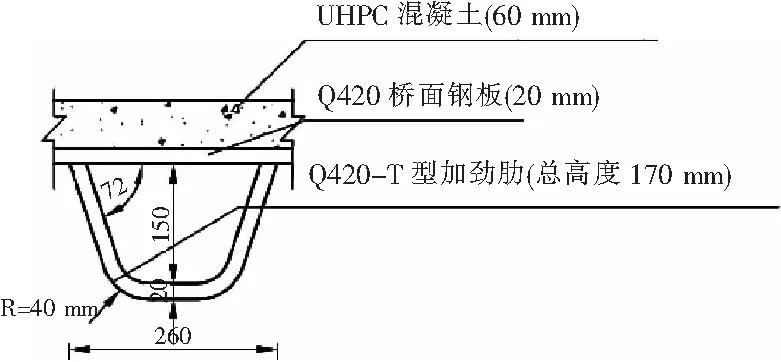
图19 U肋对比方案剖面示意

图20 设计方案挠度云图
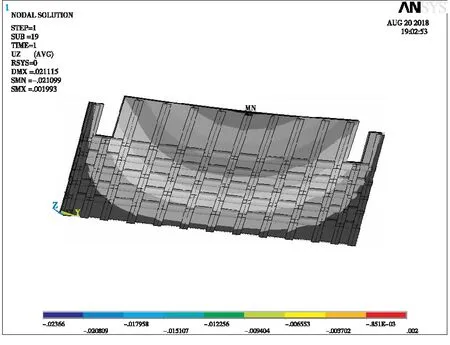
图像21 U肋对比方案挠度云图
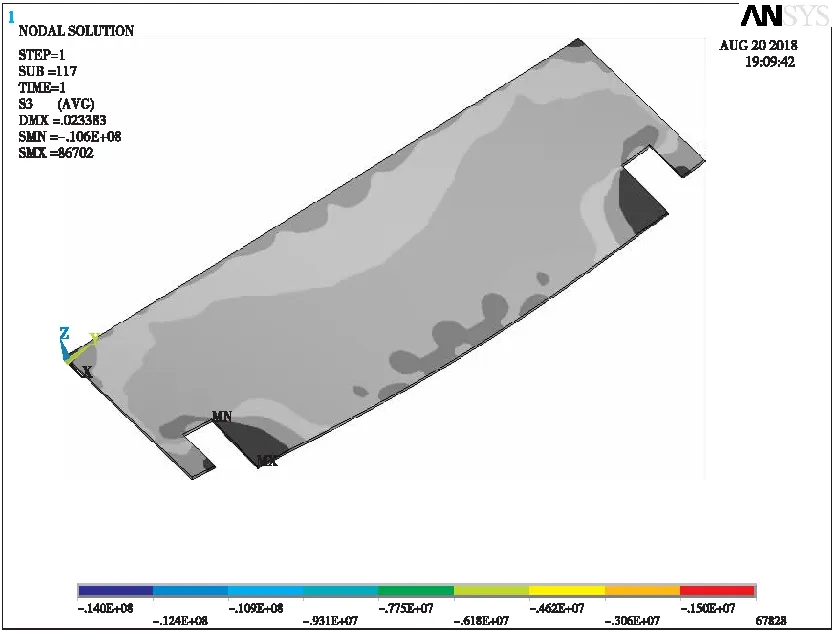
图22 设计方案混凝土压应力云图
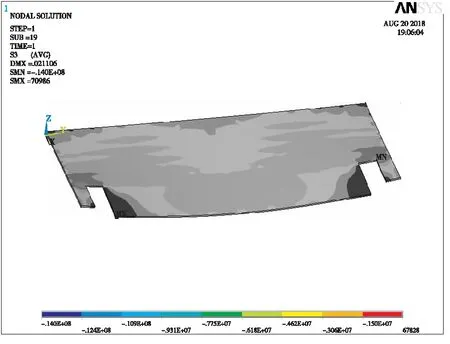
图23 U肋对比方案混凝土压应力云图
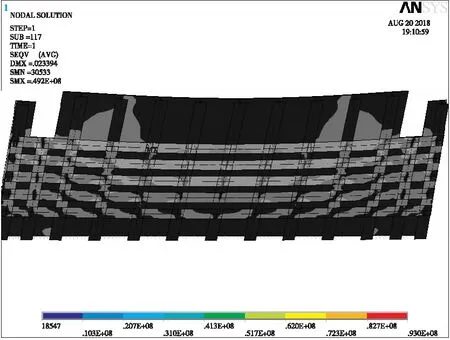
图24 设计方案钢结构米塞斯应力云图
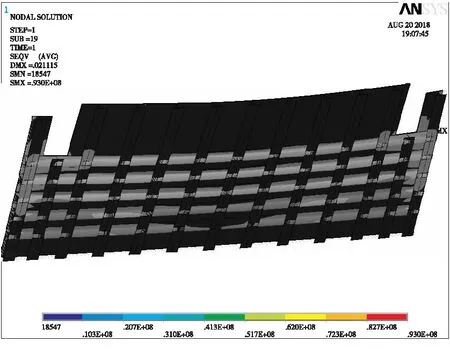
图25 U肋对比方案钢结构米塞斯应力云图
4 总 结
根据本文分析讨论,可以得出以下结论:
(1)相对于固定的约束方式,在挠度能够满足要求的前提下,采用搭接支承的方式能够有效避免钢-UHPC 组合桥面板支承范围内的应力集中现象。
(2)当混凝土厚度在6~8 cm之间时,钢-UHPC组合桥面板跨中混凝土压应力最小。
(3)钢-UHPC组合桥面板在两侧几何变化区域出现应力集中现象。相对于U型加劲肋, T型加劲肋桥面板虽然挠度较大,但能够有效减轻桥面板几何变化区域内的应力集中现象。

