城市景观斜拉桥的设计索力优化技术研究

刘朝晖，刘雪松，谭满江，薛明生

(中国电建集团中南勘测设计研究院有限公司，湖南 长沙 410014)

0 前 言

斜拉桥的索力确定是斜拉桥定量设计的一个关键步骤，由于对城市景观斜拉桥的造型要求，其结构布置往往表现出一定的“非规则性”，如桥塔倾斜弯曲、主梁布跨不对称等，这些会使索力优化过程变得复杂。

目前，用于斜拉桥索力优化的方法比较多，大致归为两类。一类是从力学平衡的概念出发，先假定最优索力方案对应于某一特定的受力状态，比如刚性支承连续梁、稳定张拉力、弯曲能量最小等，然后反推达到该状态所需要的索力，即最优索力。这类方法的优点是力学概念明确，能快速获得一个大致合理的结果；缺点是当结构有较强的非线性(如收缩徐变、施工步骤等)、非规则因素时，处理起来比较繁琐，需要较多的人工干预。另一类是从数学优化的概念出发，以设计控制指标(如梁塔各点应力、斜拉索索力等)直接作为优化控制目标，通过优化过程同时求得最优索力和相应的受力状态。虽然该方法力学概念相对不够明确，需要配置的数据更多，但是能够适应非线性、非规则情况，避免人工干预，在精细调整时能显著减少工作量。

1 背景工程

某城市景观斜拉桥为(70+192+110) m混凝土斜拉桥(见图1)。其主梁为预应力混凝土结构，采用C55混凝土，斜腹板单箱五室截面(见图2)，边孔箱室内设压重；梁高2.6 m，计入拉索区，其加高为2.85 m；顶宽24.5 m，底宽9.5 m，外侧为斜腹板。箱梁内设内横隔板，横隔板厚0.4 m，在中箱室锚固区加厚至0.5 m，每道拉索处各设一道。箱梁标准段顶板厚28 cm，中间拉索区顶板加厚50 cm；底板、斜腹板厚度均为28 cm，中腹板厚40 cm，边腹板厚25 cm。在低塔位置，主塔从主梁顶底板开洞穿过，在高塔位置，主梁与桥塔固结。

图1 (70+192+110)m混凝土斜拉桥布置(单位：mm) 图2 主梁断面(单位：mm)

主塔横桥向采用独柱型桥塔，呈天鹅颈部外形，下塔柱采用变截面直线形式，上塔柱等截面段顺桥向采用圆曲线形状。低塔高度为83 m，标准截面为440 cm×350 cm矩形，顺桥向壁厚1 m，横桥向壁厚0.7 m；高塔总高度为102 m，标准截面为500 cm×380 cm矩形，顺桥向壁厚1 m，横桥向壁厚0.8 m，索塔主体结构采用C50钢筋混凝土。塔冠采用简化的天鹅首造型，用Q235B钢材制作。

斜拉索采用Φs15.2 mm高强低松弛PE镀锌钢绞线，标准抗拉强度fpk为1 860 MPa，在塔上为锚固端，在梁上斜拉索锚固位置设置混凝土锚块作为张拉端。低塔侧设11对斜拉索，高塔侧设14对斜拉索，共计50根。主桥采用“固结+半飘浮”结构体系：高塔处采用塔梁墩固结，低塔处设置纵向活动支座和横向抗风支座，桥台处设纵向活动、横向固定支座。

上部结构的主要施工步骤如下：

(1)支架现浇施工主梁0、1号(1’号)节段，低塔处塔梁临时固结；

(2)挂篮悬浇施工主梁低塔侧的2～8号(2’～8’号)、高塔侧的2～11号(2’～11’号)节段；

(3)支架施工边孔现浇段，边孔合龙；

(4)挂篮悬浇施工主梁低塔侧的9～11号、高塔侧的11～14号节段；

(5)拆除边孔现浇支架及塔梁临时固结；

(6)中孔合拢，二次张拉斜拉索；

(7)施工桥面二期恒载。

该桥受力较为复杂，进行索力优化时要综合考虑诸多因素，例如：桥塔的曲线导致两边拉索受力不对称，高塔固结、低塔半飘浮带来的塔、梁受力不对称，边跨现浇支架和临时固结造成的多次体系转换等。

2 索力优化

2.1 基于力学平衡的方法

初步设计时，根据一次成桥的分析结果进行优化。按刚性支承连续梁方法可以使主梁和斜拉索的受力基本合理，但由于桥塔有曲线，仅考虑主梁弯矩的优化将导致桥塔弯矩达88 495 kN·m，不太合理。综合考虑塔、梁受力，经过较多手工调整后得到一个合理的受力状态(见图3)，桥塔弯矩27 000 kN·m，同时主梁弯矩比较合理，斜拉索索力较为均匀。

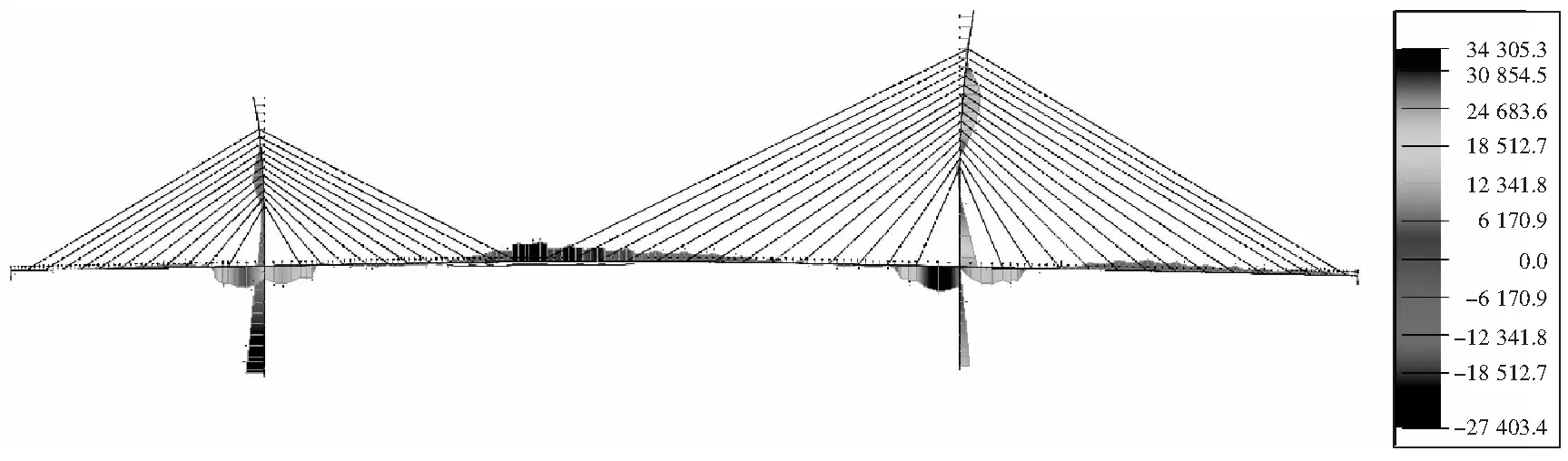
图3 一次成桥索力优化的弯矩示意(单位：kN·m)

施工图设计时，应根据模拟施工过程的分析结果进行优化。由于施工过程中存在多次体系转换，基于一次成桥状态反推得到的索力，代入后无法直接闭合，需要在施工步骤中增加额外的临时调节措施。另一方面，为了使混凝土主梁在各个施工阶段的应力满足要求，斜拉索的索力往往不能在本节段施工时张拉到位，需要在之后进行补张拉，这也会使问题变得复杂。鉴于以上原因，在模拟施工过程的索力优化过程中，不得不在一些步骤采用“人工干预”的方式，且由于需要考虑的变量和控制因素数目较多，工作量较大，效果难以保证，而利用该方法可得到一个基本满意的结果(见图4)。施工过程和成桥后的梁、塔受力较合理，但斜拉索索力略微不均匀，且斜拉索二次补张拉的根数(32根)偏多，边支点支反力储备偏小。

2.2 基于数学优化的方法

进行模拟施工过程的索力优化时，为了避免直接干预斜拉索索力带来的繁琐工作，本文采用数学优化的方法来处理索力优化中涉及的数量关系及控制条件。

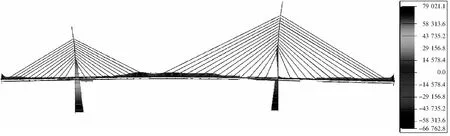
图4 模拟施工过程中索力优化结果的弯矩示意(单位：kN·m)

2.2.1 优化变量和控制量

优化变量X为结构设计中的“可调力”组成的向量，如斜拉索的张拉力、压重的重量、顶推力等。优化控制量Y(X)为结构设计中“控制指标”组成的向量，可以为结构响应量(如某一施工阶段或组合下的内力、应力、位移等)，也可以为非结构响应量(如压重量、相邻索力差值、二次补张拉索的根数等)。将Y在当前状态X0展开得：

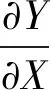
2.2.2 优化模型及求解

约束条件：对变量X和控制量Y的每个分量，按照设计要求列出约束条件即可，例如对主梁应力组合值Yi，约束条件为σmin≤Yi≤σmax。

目标函数：可以从结构响应量构造(如最小弯曲能量)得到，也可以从变量和非结构响应量构造(如索力均匀性、二次张拉斜拉索的数目或边孔压重数量等)得到。斜拉桥索力优化的数学模型具有变量数较多、约束条件多且一般为线性的特点，可采用常规优化算法求解。

2.2.3 应 用

采用上述基于数学优化的方法，对该城市景观斜拉桥进行索力优化，主要设置条件见表1。构造的数学优化模型属于混合整数线性规划类型，采用内点法求解。为了消除收缩徐变影响，优化过程中进行了2～3次迭代结构分析，最终索力及压重由优化求解得到，无需任何手工调整。

2.3 结果比较

运用基于数学优化的方法，得到的结果见图5～7。施工阶段和成桥后的梁、塔、索受力均有明显改善。

表1 索力优化的设置条件

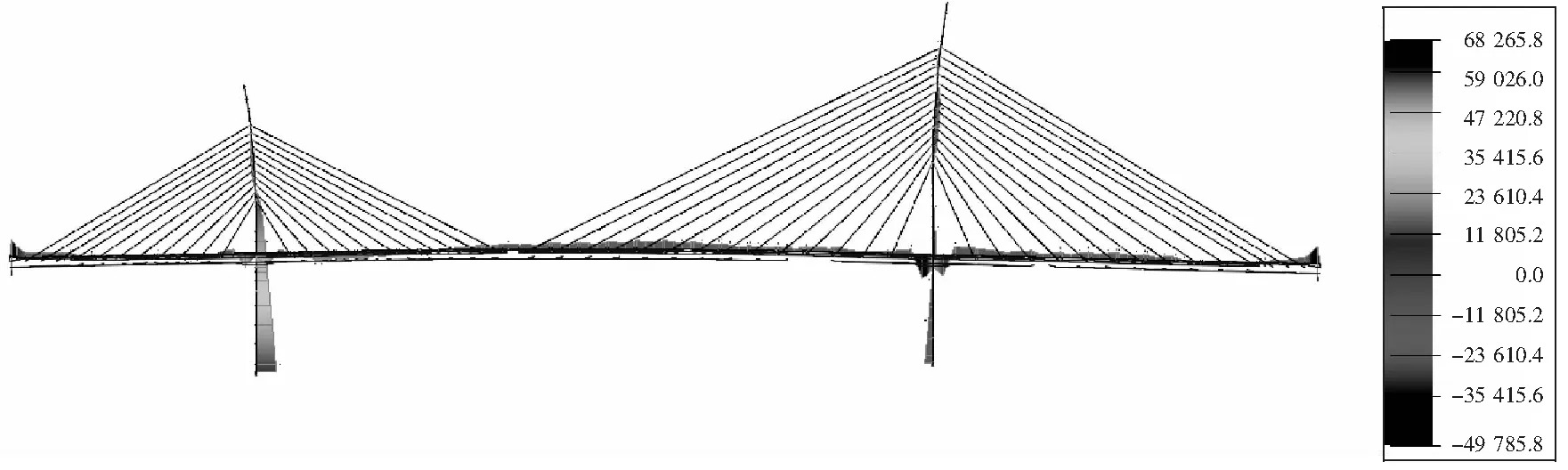
图5 模拟施工过程的索力优化结果的弯矩示意(单位：kN·m)

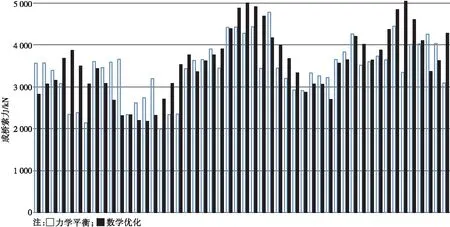
图6 成桥索力比较

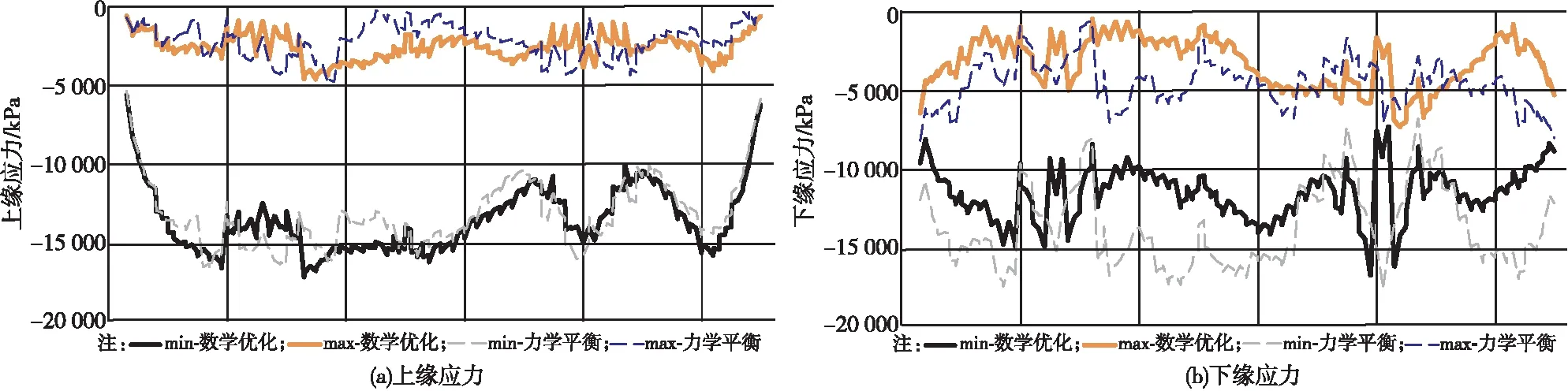
图7 运营阶段主梁应力比较

(1)施工阶段主梁最大拉应力由0.8 MPa减小到0.2 MPa，最大压应力由16 MPa减小到14.2 MPa。

(2)运营阶段主梁压应力储备由0.4 MPa增加到1 MPa。

(3)斜拉索索力更加均匀，相邻索力差值由1 500 kN减少到500 kN。

(4)桥塔最大压应力由17.0 MPa减小到16.2 MPa。

(5)斜拉索二次补张拉索的根数大幅减少，由原先的32根减少为5根。

(6)临时固结处剪力和边支点支反力均满足要求。

3 结 论

针对城市景观斜拉桥造型独特、受力复杂的特点，本文运用了基于数学优化的方法进行索力优化，将斜拉桥施工过程和成桥运营阶段的控制条件全部集中到数学优化模型中，实现了一次求解即得到最终的索力结果。此方法无需手工干预，减少了工作量，求解得到的结果显著优于传统的基于力学平衡方法得到的结果。