基于加权遗传算法的双目标应急物资配送车辆路径优化决策模型
宋英华,尹思杨,杜丽敬
(1.武汉理工大学安全科学与应急管理学院,湖北 武汉 430070;2.武汉理工大学中国应急管理研究中心,湖北 武汉 430070;3.武汉理工大学安全预警与应急联动技术湖北省协同创新中心,湖北 武汉 430070)
近年来地震灾害愈发频繁,已经成为威胁人类生命和财产安全的主要地质灾害。如2008年我国汶川地震,共造成69 227人死亡、374 643人受伤、17 923人失踪,是我国唐山大地震后伤亡最严重的一次地震;2010年我国青海玉树地震,共造成2 220人遇难、70人失踪,同时上万人在地震中受伤以及大量房屋受损;2011年日本大地震,共造成15 985人死亡、13 346人失踪,而且引发的巨大海啸对日本东北部岩手县、宫城县、福岛县等地造成了毁灭性破坏,并引发福岛第一核电站核泄漏。地震灾害发生后在短时间内会造成大量的人员伤亡,如果不及时向灾区配送足量的应急药品,可能会引发灾区大规模传染病的暴发以及灾民死亡人数的大幅度增加,因此将药品及时、有效地运送到受灾点至关重要。
车辆路径安排是应急物资配送的核心。然而执行具体的应急物资配送的是车辆的驾驶员,一方面驾驶员要面临地震后的余震风险和复杂的道路条件;另一方面驾驶员还要承受着灾难发生后大规模传染病暴发对自己的威胁以及地震造成的惨烈场景对自己内心的冲击,因此驾驶员的心理安全程度对应急药品能否被准确、高效地运送到受灾点起到决定性作用。张圆等[1]为了研究影响男女驾驶员安全的不安定因素,以广东省9 886条小型轿车交通事故数据为基础,对比分析了不同性别驾驶员的交通事故特征,并以交通事故严重程度为因变量,将其分为严重事故和非严重事故,从14个候选自变量中筛选出对不同性别驾驶员交通安全具有显著影响的自变量因素,采用二项Logit模型分别建立了男、女性驾驶员交通事故严重程度预测模型,同时对模型参数进行估计与检验,最终确定对不同性别驾驶员交通事故严重程度均有显著作用的影响因素有驾驶员是否系安全带、车辆有无保险、道路安全属性、路口路段类型和照明条件等。另外,为了最大程度地避免灾区流行病的暴发和蔓延,政府应急救援部门必须要给整个配送活动设置一个柔性时间窗,对超过该时间窗上限的每一分钟增加惩罚性成本,以期实现时间惩罚成本最小,因此时间惩罚成本也作为本文考虑的一个目标。
从应急物流心理感知的角度考虑,Hu等[2]制定了多目标线性规划模型,能够系统、最大限度地降低总体逆向物流成本、相应的环境和运营风险以及当地居民的心理创伤,并且利用结构化方程模型比较了处理灾后碎片的工作人员与受灾的灾民之间的心理成本变化的差异性;Hu等[3]研究认为受灾者所感受到的心理惩罚成本在等待灾区撤离或庇护所救济资源时可能会增加,而心理干预可以降低感知心理成本的幅度,并且开发了多步骤疏散和避难的新数学模型用以实现配送成本和心理惩罚成本的最小化;Sheu[4]从需求者的角度出发,根据生存心理学和认知理论,假设了灾后幸存者的感知—态度—韧性关系,并进行了规范分析,其中包括基于提出的概念模型和假设,建立幸存者特定的分解态度函数和灾后救济服务分布优化模型,同时使用结构方程模型验证了感知—态度—需求模型的有效性,该研究旨在实现救灾服务的分配,以最大限度地提高幸存者的适应能力。针对灾害发生后,由于临时避难所数量和住房建设能力不足,必须将受害者分批疏散和重新安置的情况,Hu等[5]构建了一种新的混合整数线性模型用于多步骤疏散和临时安置,以实现由恐慌诱发的心理惩罚成本、心理干预成本以及与运输和建筑物避难所相关的成本最小化。为了更好地解决可能出现的配送时间窗更改、送货地址变化等动态扰动问题对需求者的影响,宁涛等[6]构建了基于前景理论的价值函数度量策略来更好地感知需求者的心理感知变化。
从车辆路径问题和多目标优化求解的角度考虑,Oruc等[7]开发了一个双目标数学模型,旨在通过提供受损害信息来增加评估道路的总体价值和最大化评估节点的总利润,可以有效地寻找救援线路;Akbari等[8]开发了一个精确的混合整数规划(MIP)公式以及一种基于MIP-relaxation和局部搜索算法的数学方法,用来解决由于灾后碎片堵塞而造成的路径无法通行的问题,实现重新获得网络的连通性和基于道路的可通行性从而选择应急物资车辆的配送线路;Wang等[9]构建了一个非线性整数开放位置-路径模型,用以实现旅行时间和总成本的最小化以及分割交付的可靠性,并利用非支配排序遗传算法和非支配排序差分进化算法来验证所提出模型的有效性;Bozorgi-Amiri等[10]提出了一个多目标动态随机规划模型,用于解决灾前和灾后决策的人道主义救援物流问题,该模型具有三个目标,即最大限度地减少所有时期受影响地区之间的最大短缺量、总旅行时间以及灾前和灾后成本,最终将所提出的模型转化为应用ε-约束方法的单目标混合整数规划模型进行求解;杜战其等[11]以特大型港口上海洋山港为例,总结了在港口应急事件下应急车辆调度问题所具有的特性,着重考虑了时效性、经济性和安全性三个特性,并将包含时效性、安全性和经济性三个属性分量的多属性决策模型进行了无量纲化处理,最终求取决策效用函数,并利用改进路径优化算法进行求解,得到了一些启示性建议;刘长石等[12]构建了以所有车辆的碳排放量最小为目标的低碳时变车辆路径问题数学模型,通过引入交通拥堵指数,设计交通拥堵规避方法,并根据模型特点设计了一种改进的蚁群算法进行求解,最终实现了有效规避交通拥堵、缩短车辆行驶时间、减少车辆碳排放、促进物流配送与生态环境的和谐发展;徐君翔等[13]开发了以总配送时间最短为目标的数学模型来研究考虑动态行驶时间的无人驾驶车辆的路径问题,指出动态行驶时间与时变速度相关,并利用遗传算法验证了该数学模型的准确性和设计算法的优越性;马艳芳等[14]考虑运行环境的不确定性、顾客时间窗口要求以及对顾客同时进行取货和送货服务的情况,构建了不确定VRPSPD数学模型,以实现运作成本最低和顾客满意度最高的决策目标;饶卫振等[15]通过研究协作配送模型与成本分摊方法,构建了多方协作车辆路径问题模型,分析了协作配送成本分摊问题的属性,并基于经典的Shapley成本分摊方法,提出了B-T (Binary Tree) Shapley近似方法,从而能够在合理的时间内完成协作配送问题的成本分摊,最终实现显著地降低物流配送成本和减少尾气排放的目标;肖建华等[16]针对日益严峻的城市汽车尾气污染问题和日趋严格的城市限行措施,开发了基于城市道路限行的多能源多车型混合车辆路径优化模型,并将城市分区域、分车型等限行因素引入到车辆路径问题,以实现碳排放、运输等费用总成本最小的目标。
通过分析上述研究成果可以看出,研究动态多目标的车辆路径问题已经成为当今应急物流领域研究的主要问题。从研究角度来看,目前大多数研究都是从物流组织者的角度出发研究整个物资配送活动的成本、时效性和可靠性,但是对于具体执行物资配送活动的驾驶员的心理状态研究相对较少;从研究的方法来看,目前的模型多是以单一目标函数为主,针对目标变化而进行的分段研究较少;从研究的意义来看,将驾驶员的心理成本纳入震后初期应急物资配送成本中,可以有效地增加应急物资配送的安全性和有效性,对灾后重建和灾区社会秩序的稳定具有重大意义。因此,本文主要研究震后初期受灾点对药品需求下基于驾驶员心理成本和时间惩罚成本最小化的配送中心到受灾点的车辆配送路线安排问题。
1 问题描述与建模
1.1 模型假设
考虑驾驶员心理成本的应急车辆路径决策模型假设如下:①配送中心与受灾点的地理位置已知,且道路的通行情况可以通过探测技术实时获得;②每台配送车辆只装载应急药品这一种物资,与此同时,其他种类的物资不可以通过这些车辆进行配送;③配送的交通工具默认为是同一种型号的卡车,其他交通工具,例如飞机、轮船等不予以考虑;④每台配送卡车上固定搭配两名驾驶员,在配送过程中默认经过每个受灾点时驾驶员可以进行短暂休息但不进行人员更换;⑤默认每辆车装载的药品可以满足设计的配送线路各受灾点的物资需要,不考虑拆分配送和物资需求量短缺的情况。
1.2 问题描述
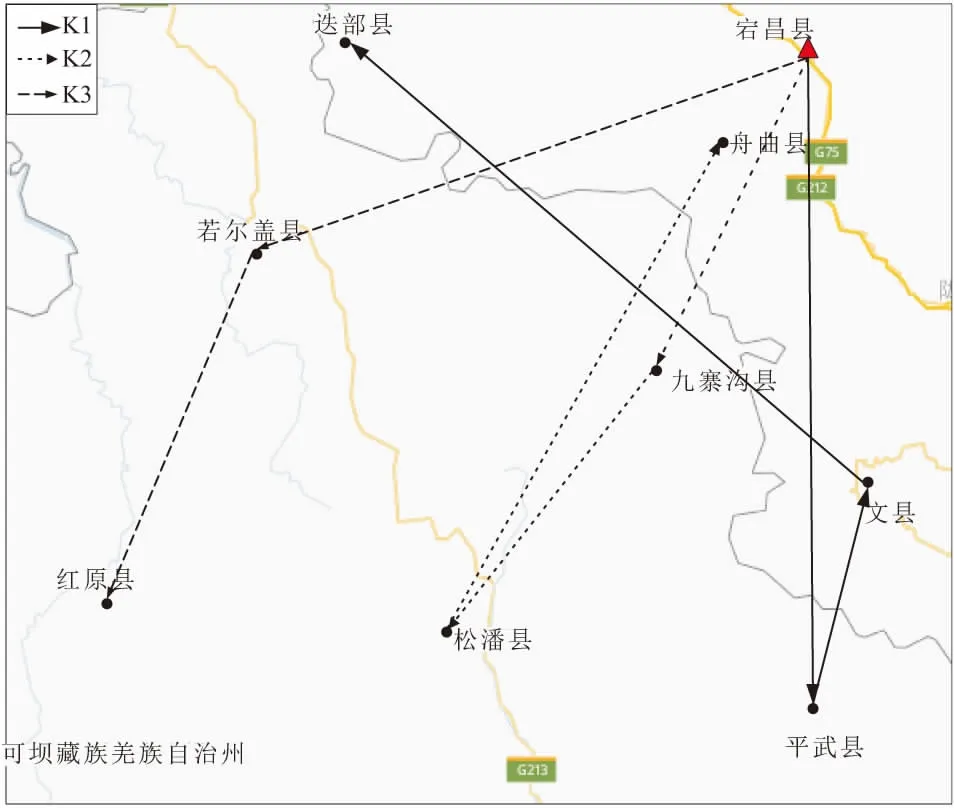
在考虑驾驶员心理成本的应急车辆路径决策模型中,应急物流网络表示为G=(V,A),如图1所示。其中,V包含两个子集,为选定的应急物资配送中心M和受灾点集合N;A为可用链路集合。D=(dij)为各点之间的距离矩阵[(i,j)∈A],其中i、j属于配送网络中的点,k代表车辆,满足三角不等式,即对任意i,j,k∈V都有dij 图1 应急物流系统VRP示意图Fig.1 Vehicle Routing Problem(VRP) illustration graph of emergency logistics system 考虑驾驶员心理成本的应急车辆路径决策模型中,用到的其他符号和变量定义如下: n为受灾点数量(个);m为选定的配送中心数量(个);L为应急物资集合量(t);l为应急物资索引,l∈L;Ql为应急物流系统中物资l的配送量(t);Qijk为车辆k从受灾点i到受灾点j的物资配送量(t);K为所有车辆(线路)的集合(条);k为车辆的数量(台);tk为车辆运行的总时间(min);ti为车辆到达受灾点i的时间(min),i∈n;t0为驾驶员心理发生变化的时间临界点(min);C0为灾害发生后参与配送的驾驶员的初始心理成本(元);tr为驾驶员每到达一个受灾点的休息时间(min);S0为驾驶员心理变化点之前给予的固定薪酬(元);S1为驾驶员的驾驶时间超过心理变化临界点后多驾驶每1分钟所给予的补偿工资(元);Ps为驾驶员薪酬的心理补偿系数;Pr为驾驶员每到一个受灾点休息的心理补偿系数;Ci为驾驶员到达受灾点时的心理成本(元);Cs为驾驶员心理总成本(元);t1为物资配送时间窗所要求的上限时间(min);Ct为超过时间窗上限的单位车辆配送时间惩罚成本(元);Cp为车辆配送时间惩罚总成本(元);Cj为单个受灾点的车辆配送时间惩罚成本(元)。 其中,决策变量为: yijk:1,车辆k从受灾点i运送物资到受灾点j;0,否则[k∈K,(i,j)∈A]。Zmk:1,车辆k从配送中心m出发;0,否则[k∈K,m∈M]。xm:1,选定的配送中心开启;0,否则。 建立驾驶员心理成本的模型需要从三个角度进行考虑:第一个角度是测算驾驶员驾驶车辆经过每一个受灾点的心理成本,并使之尽可能地增大,这样有助于最终决策的科学性和实用性;第二个角度是计算驾驶员的薪资报酬对驾驶员心理成本的影响,如肖琴等[17]构建了空中交通管制人员薪酬满意度对安全绩效影响的概念模型,由于薪酬满意度与员工工作不安全感呈显著负相关关系,所以薪资报酬的增减会对驾驶员的心理产生影响,因此给予驾驶员丰厚的薪水可以最大程度地降低驾驶员在行驶过程中的心理成本;第三个角度是计算驾驶员每到达一个受灾点的休息时间对其心理成本的影响,如史晨军等[18]构建了基于扩展计划行为理论(Ex-TPB)的驾驶员疲劳驾驶行为结构方程模型(SEM),从社会心理学角度探讨了影响驾驶员疲劳驾驶行为的心理因素以及各因素间的相关关系,因此确保驾驶员到达一个受灾点后有足够的的休息时间对降低驾驶员的心理成本至关重要。后两个角度是为了最大程度地降低第一个角度的驾驶员心理成本值,使得驾驶员在物资配送过程中心理成本保持在一个较低的水平,有利于物资配送过程的高效、安全,最终使得驾驶员的心理总体成本最小。 在设计好的线路中,由于每台车辆从第一个受灾点行驶到最后一个受灾点不用返回配送中心,所以驾驶员到达每一个受灾点的驾驶时间是从上一个受灾点到下一个受灾点的时间。 首先,假定车辆从配送中心出发的时间为0,即对xm=1、Zmk=1(m∈M,k∈K),有tmk=0。根据前景理论,可以推导出驾驶员经过每个受灾点的数学模型,即: 为了量化心理成本权重因子,α为驾驶员实际工作时间小于心理变化临界点的权重因子,μ、β为驾驶员实际工作时间大于心理变化临界点的权重因子,这些权重因子是根据驾驶员在这个阶段的心理状态确定的。例如在ti≤t0这个阶段,驾驶员的工作刚刚开始,积极性也较高,因此在这个阶段驾驶员的心理处于一个“保守”的状态,由模型来看,驾驶员的心理成本和驾驶时间呈正相关的关系,在确定权重函数α时,就选取一个较低的数值;反之,μ、β值的选取也是按照这个原则确定。 其次,考虑薪酬作为影响驾驶员心理感知的一个重要因素,可将薪酬纳入到心理成本考虑范围,于是可以推导出一个线性数学模型,即: 该模型主要是研究驾驶员心理变化临界点前后薪资水平对驾驶员心理成本的影响,其中Ps∈(0,1)。 最后,考虑驾驶员经过一个受灾点进行休息的时间对驾驶员心理成本的影响。在这里将驾驶员的休息时间tr设置成一个固定参数值,于是可以得出一个数学表达式Pr×tr,其中Pr∈(0,1)。因此,当ti≤t0时,有Ci=-(t0-ti)α+C0-Ps×S0-Pr×tr;当ti>t0时,有Ci=μ(ti-t0)β+C0-Ps×[(ti-t0)×S1+S0]-Pr×tr。该模型默认在应急物资配送过程中驾驶员到达上一个受灾点的心理成本不重复累加到下一个受灾点,因此所有车辆中驾驶员在应急物资配送中的心理总成本的数学模型可以表示为 除此之外,再计算物资配送的时间惩罚成本,通过设置一个物资配送时间窗,如[0,t1],如果车辆运行总时间tk超过物资配送时间窗的上限,那么超出的每1分钟都需乘以单位车辆配送时间惩罚成本,作为整个配送活动的车辆配送时间惩罚成本。如果tk≤t1,那么单个受灾点的车辆配送时间惩罚成本Cj=0;如果tk>t1,则Cj=(tk-t1)×Ct。配送活动的车辆配送时间惩罚总成本的数学模型可以表示为 s.t. (1) xm=1(m∈M) (2) (3) (4) (5) tijk≥0(i,j∈N;∀k∈K) (6) Ci≥0(i∈N) (7) yijk=0或1(i,j∈N;∀k∈K) (8) 上式中:约束(1)表示的是车辆在每两个受灾点间服务的时长不超过总体服务时间;约束(2)表示的是配送中心处于开启的状态且位置已知;约束(3)表示每两个受灾点之间的物资配送量小于实际车辆总体配送量;约束(4)表示如何确定具体的一个受灾点i的实际物资配送量;约束(5)表示车辆配送的物资量不会超过物资的总量;约束(6)和(7)表示驾驶员驾驶车辆从受灾点i到j的时间和驾驶员到达每个受灾点的心理成本为正数;约束(8)为0-1整数变量约束。 本文将采用加权遗传算法对双目标应急物资配送车辆路径优化决策模型进行求解,相比于普通的遗传算法,加权遗传算法可以将双目标问题转化为单目标问题进行求解,可以设置m1、m2为驾驶员心理成本和车辆配送时间惩罚成本的权重因子,确保m1+m2=1,于是可以得到一个新的目标函数,例如加权后的最优目标函数值=m1×加权后的驾驶员心理成本值+m2×加权后的车辆配送时间惩罚成本值,这样每个配送方案只会生成一个目标函数值,有助于将问题简化并得到近似全局最优解。 计算驾驶员的心理成本是为了帮助决策者更好地选择应急物资配送路径。因此编码产生的结果是车辆的配送路径,在编码中将采取实数编码的形式,在配送中假定有3辆同型号卡车对灾区进行配送,分别编号为1、2、3;假定有10个受灾点需要配送服务,将1、2、3号车随机地排列在10个基因位上。下面列举一个例子,演示一下具体的配送方法,例如染色体(1,3,2,2,3,1,2,1,1,3),每台车辆所在基因位的顺序就是这台车辆的配送路径,所以这个染色体代表的配送方案为1号车:0→1→6→8→9;2号车:0→3→4→7;3号车:0→2→5→10。其中,0代表已选定的配送中心,这样一个配送方案就产生了,通过设置种群规模就可以得到数量相同的配送方案,至此,种群初始化的工作就已经完成。 首先要设置一个交叉概率Pc,再随机生成一个随机数,用来与Pc比较,如果随机数小于交叉概率,那么需对染色体执行交叉操作。具体的交叉操作过程为先确定一个交叉点,将两条染色体交叉点之后的元素进行交叉,这样就得到了两个全新的染色体。 同样还要设置一个变异概率Pm,在变异操作中要对每条染色体确定两个变异点,然后将两点之间的元素进行逆向交换,得到一个全新的染色体,从而完成变异操作。 首先根据驾驶员心理成本模型编制适应度函数,并且将每条染色体代入适应度函数中,根据目标函数值由小到大进行排序,每次迭代保留最优染色体,从而得到近似最优解。 加权遗传算法的基本步骤如下(见图2): 图2 加权遗传算法流程图Fig.2 Flow diagram of the weighted genetic algorithm 步骤1:通过初始化操作得到初始种群NIND,染色体个数为NP个。 步骤2:设置迭代次数。 步骤3:对初始化的染色体执行交叉操作。 步骤4:对交叉操作后的染色体执行变异操作。 步骤5:设置适应度函数adapting1,计算每条染色体的适应度并且找出最优染色体加以保存。 步骤6:对迭代完后得到的每一代精英染色体进行适应度加权计算并排序。 步骤7:选取近似最优染色体。 步骤8:终止操作。 四川省阿坝州九寨沟地震共造成25人死亡、525人受伤、6人失联、176 492人(含游客)受灾,73 671间房屋不同程度受损(其中倒塌76间)。本次的研究对象为地震发生后第一天受灾最为严重的8个地区,其中受灾点1~8分别为1(九寨沟县)、2(若尔盖县)、3(红原县)、4(松潘县)、5(平武县)、6(文县)、7(舟曲县)、8(迭部县),受灾区域地理信息分布图见图3,选定的配送中心为宕昌县,假设配送中心与受灾点之间以及各受灾点之间的道路均可通行,每台车辆所搭载的药品数量也足够满足该车辆所经过的受灾点的需要且每台车辆在配送过程中保持相同的行驶速度(80 km/h)。为了研究整个配送过程的车辆配送时间惩罚成本和驾驶员心理成本,给出了驾驶员从配送中心(宕昌县)到8个受灾点的时间和驾驶员从受灾点到受灾点所用的时间,见表1和表2。同时,为了最大程度地衡量驾驶员心理成本对配送方案的影响,赋予驾驶员心理成本一个较大的权重值,这样可以将每个配送方案的驾驶员心理成本最大限度地刻画出来,决策者可以根据驾驶员心理成本的大小选择最优配送方案。本文采用加权的方法对目标函数中的车辆配送时间惩罚成本和驾驶员心理成本赋予两个不同的权重因子m1,m2∈(0,1),其中赋予车辆配送时间惩罚成本的权重因子m2=0.01,赋予驾驶员心理恐慌成本的权重因子m1=0.99。依据驾驶员在不同阶段的心理状态(根据第1.4节中确定的方法原则),随机设置了α、β、μ、C0、Ct,随后以3 h作为柔性时间窗的上界,将驾驶员心理发生变化的时间临界点和薪酬设置为100 min和3 000元,避免驾驶员的心理成本由于薪酬、休息的原因被过分地缩小,并根据休息时间和薪酬的大小选取了它们各自的权重系数,然后将μ=0.9、α=0.1、β=0.5、t0=100、t1=180、C0=4、Ct=5、S0=3 000、S1=10、Ps=0.001、Pr=0.1、tr=30各项参数输入计算机。 图3 受灾区域地理信息分布图Fig.3 Geographical information distribution map of the disaster area 表1 驾驶员从配送中心到8个受灾点所用的时间 (单位:min)Table 1 Driving time of drivers from distribution center to eight disaster areas(unit:min) 注:“0→1”表示驾驶员从配送中心到第1个受灾点所用的时间(其中“0”表示配送中心);其他含义同。 表2 驾驶员从受灾点到受灾点所用的时间(单位:min)Table 2 Driving time of drivers between disaster areas(unit:min) 本文采用Matlab R2014a对算法进行编程,所有计算工作在同一台计算机上完成,所使用的计算机的性能参数见表3。经过多次试验,加权遗传算法控制参数设置为:种群规模NP=60,变异概率Pm=0.7,交叉概率Pc=0.9。 表3 计算机的配置参数Table 3 Computer configuration parameters 通过对该算法不合理因素进行修正后,具体的最小配送总成本迭代图和最优配送方案的车辆配送路线图,见图4和图5。其中,图4为基于目标函数的每一代目标函数值相较于上一代目标函数值而得到的最优解的迭代过程,即最小配送总成本的变化过程;图5为根据图4所得到的最优配送方案的车辆配送路线图。 图4 最小配送总成本迭代图Fig.4 Iteration graph of the least total cost of distribution 图5 总成本最小化配送方案的车辆配送路线图Fig.5 Vehicle distribution routing of the distribution scheme with the least total cost 由图4可见,加权后的目标函数值迭代到第105次以后开始出现收敛的状态,从第105次到第200次迭代的目标函数值趋于稳定,即得到近似最优解。 由图5可见,宕昌县作为灾后应急物资的配送中心(3台配送车辆的出发地),具体的配送方案为:K1车辆的路径为宕昌县→平武县→文县→迭部县;K2车辆的路径为宕昌县→九寨沟县→松潘县→舟曲县;K3车辆的路径为宕昌县→若尔盖县→红原县。这个近似最优解中车辆配送时间惩罚成本为5 895.5元,驾驶员心理成本为29.2元。 地震发生后,会造成大量的人员伤亡和财产损失,同时也极易爆发瘟疫等严重传染病,因此将急需的应急药品配送到灾民手中便成为了此时车辆路径问题(VRP)的核心。由于地震刚刚爆发,驾驶员在配送的过程中可能会面临余震和传染病感染的风险,因此政府和相关社会救援组织要从驾驶员心理安全性和车辆配送时间惩罚成本的角度设计规划应急物资配送路径,以期最大程度地降低震后初期的应急物资配送成本和提高整个配送过程的安全性。 本文研究了地震后路网完全畅通条件下的应急车辆路径问题,考虑向灾区运送药品(车载物资完全能够满足受灾点的需要),不考虑需求量的问题,采用3辆同型号车辆,运用前景理论的知识构建了驾驶员心理成本模型和车辆配送时间惩罚成本为目标的应急车辆路径数学模型,并采用加权遗传算法(GA)求解,通过调整目标函数的权重因子m1、m2以及两个模型中的各项输入参数,可以得到不同的最优近似配送方案,决策者可以根据实际情况和所配送物资的紧急程度来选择车辆路径的具体调度方案。最后以四川省阿坝州九寨沟地震作为算例,验证了该模型和算法的有效性,对灾害后应急物资配送有一定的参考价值。 由于地震后应急配送网络的动态性和随机性,将选址问题和灾民对物资配送的感受纳入到车辆路径问题的整体考虑中,将会得到更科学、有效的近似全局最优解,可进一步降低受灾区域配送人员的心理成本,这将是今后的研究方向。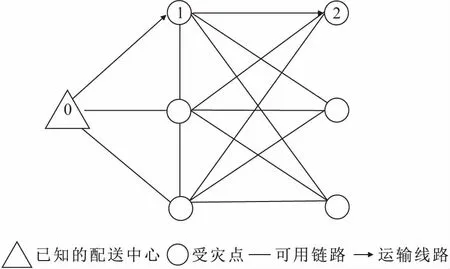
1.3 符号说明
1.4 模型的建立

2 算法设计
2.1 编码规则与种群初始化
2.2 交叉操作
2.3 变异操作
2.4 适应度计算及其排序
2.5 加权遗传算法的基本步骤

3 算例分析





4 结论与建议

