低渗透性裂隙介质中激发强度对Slug试验的影响研究
曹孟雄,陈 刚,胡 成
(中国地质大学(武汉)环境学院,湖北 武汉 430074)
Slug试验是一种通过瞬时改变钻孔内水位并记录水位变化值来推算含水层水文地质参数的现场测试方法,具有操作简单、耗时短、对含水层扰动低等特点。最早的Slug试验分析方法是由 Hvorslev[1]发明的,适用于承压含水层且忽略含水层的弹性储水效应,假定井中水位变化无加速度惯性作用,且地下水流动为稳定流运动模式;Cooper等[2]假定含水层的弹性储水效应不可忽略,且井中水位变化无加速度惯性作用,推导出第一个承压含水层Slug试验完整井的非稳定流运动模型。由于上述承压含水层Slug试验分析模式都假定井中水位变化无加速度惯性作用,因此均仅适用于分析测试井管内水位以近似指数的方式缓慢恢复的非振荡反应的试验资料。 Bouwer等[3]发展了非承压含水层Slug试验分析模式,利用测试井中滤管长度与滤管半径的比值,配合经验公式来求得其有效半径,以推估含水层的渗透系数,称为Bouwer & Rice模型。针对在高渗透性含水层中Slug试验反应曲线产生振荡的情况,Kipp[4]利用动量与质量关系得到与 Cooper等[2]相似的动量守恒方程式,用于高渗透性含水层中的振荡资料分析并求得半解析解;Hyder等[5]提出了一种可分析承压含水层和非承压含水层非完整井中Slug试验的半解析解模型,也称为KGS(堪萨斯州地质调查局)模型,并对比分析了Hvorslev[1]和Cooper等[2]的研究成果,结果表明在渗透系数相对较低的含水层中(以K<5×10-4m/s为界),Hvorslev模型得到的结果更为理想。此外,还有许多关于Slug试验振荡反应曲线分析模式的研究,这些研究考虑了测试井中水位变化因井管内扰流和水位动态压力变化而产生的非线性反应,从而发展出Slug试验非线性振荡反应曲线分析模式和分析方法[6-10]。
当前国内对于Slug试验的研究多基于国外Slug试验代表性理论模型而开展。如曾明明[11]基于Bouwer & Rice模型通过一系列的Slug试验计算出测井周围岩土体的渗透系数,并通过与抽水试验结果对比可知,两者的数值近似,表明Bouwer & Rice模型用于确定岩土体渗透系数是简便可行的;万伟锋等[12]通过建立物理模型Slug试验平台,利用Bouwer & Rice模型模拟分析了不同激发方式下不同激发强度对多孔均质含水层Slug试验结果的影响,结果表明在多孔均质介质中激发强度对Slug试验的计算结果无明显的影响,但激发强度越大,Slug试验的影响范围越大,故在现场具备快速水头变化条件的情况下,应选择较大的激发强度;苏锐[13]通过在低渗透性裂隙介质地区开展Slug试验并对与水头相关的参数进行灵敏度分析,结果表明激发强度越大,地下水流系统响应越显著,建议Slug试验采用较大的激发强度;Ji等[14]通过一系列不同激发强度的Slug试验,研究了非达西流对裂隙岩体地区Slug试验结果的影响;Wang等[15]认为瞬时改变Slug试验测试段内水位会产生比较明显的水力梯度(尤其是试验初期),这会使得钻孔周围含水层地下水出现非线性流动。
Slug试验理论模型发展相对成熟,但对Slug试验具体过程的研究较少,不同激发强度对Slug试验结果的影响鲜有报道。为此,本文在低渗透性裂隙介质中对不同平面位置采用注水式多深度分段Slug试验获取含水层水文地质参数,通过对同一试验段采用“小—中—大”激发方式开展Slug试验,利用Bouwer和Rice提出的半解析方法求取含水层的渗透系数,对比分析在不同激发强度下低渗透性裂隙介质渗透系数计算结果的差异性,并通过求取雷诺数来表征不同激发强度下钻孔附近的实际地下水流态,讨论适宜的激发强度,以为今后Slug试验在实际工程勘察中的应用提供借鉴和参考。
1 理论模型
在开展Slug试验研究时,有两方面的问题需要解决:一是对实际物理模型进行合理概化,准确分析Slug试验的影响因素;二是适用性数学模型的选取,根据地质资料以及概化后的物理模型选择相匹配的数学模型。最后将物理模型与适用性数学模型相结合,求取低渗透性裂隙介质的渗透系数。
1.1 物理模型概化
为了建立裂隙岩体中Slug试验的理论模型,需先对实际物理模型进行合理概化。国外一些学者经过深入研究,提出了两种模型概化方法:一是等效孔隙介质模型,即认为对于裂隙率高且裂隙与周围岩块没有水量交换的裂隙介质,可以将其等效为多孔介质,采用传统方法进行分析;二是替代模型,包括离散裂隙模型和双重介质模型,其中离散裂隙模型适用于裂隙率低且裂隙与周围岩块没有水量交换的裂隙介质,双重介质模型则适用于导水裂隙密度相对较高且裂隙与周围岩块存在水量交换的裂隙介质。Butler[16]、Lee等[17]研究指出,运用替代模型计算时,所需要的一系列含水层水文地质参数具有相关性,很难独立获得,且不同的参数组合可以得到相近的试验结果。由于地下水在非均质裂隙介质中流动问题的数学描述非常复杂,使得替代模型在实际运用上存在一定的困难。因此,尽管裂隙介质存在非均质性,在利用双栓塞分层试验设备在裂隙岩体中开展水文地质试验时,一般仍将野外复杂的非均质各向异性裂隙介质概化为分层均质的各向同性多孔介质(见图1),此时可运用多孔介质理论解决地下水流问题。在低渗透性裂隙介质中开展Slug试验时,其地下水渗流主要在节理裂隙中进行,基岩岩块相对于节理裂隙为弱透水介质,块状构造的岩体难以形成完整的隔水顶板,目标钻孔所选试验段上并无隔水层和弱透水层。故本文根据野外实际地质条件和试验条件提出如下概化条件:
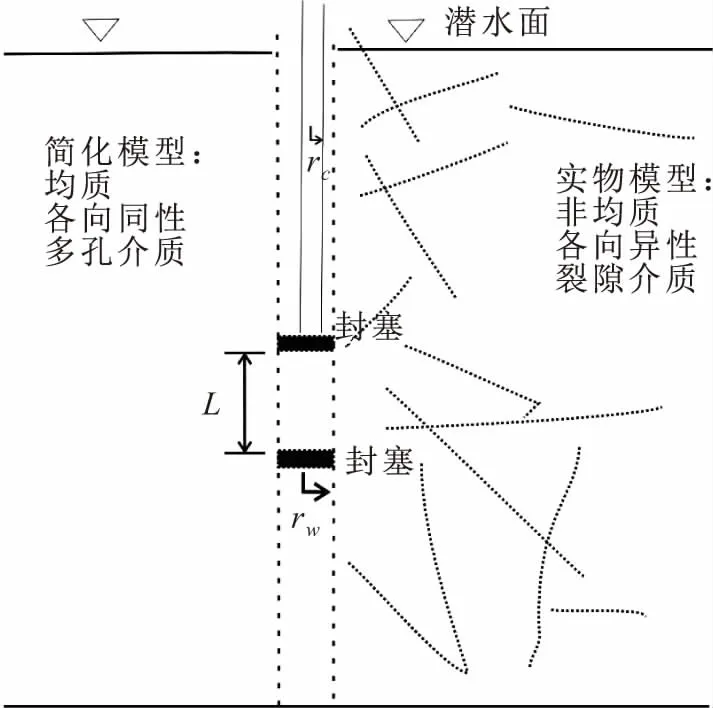
图1 裂隙含水介质物理模型概化图Fig.1 Overview of physical model of crack water medium注:L为试验段滤管长度(m);rc为套管半径(m);rw为滤管半径(m)。下同。
(1) 宏观上,将裂隙岩体看作以钻孔为轴心的无限大圆柱形潜水含水层,钻孔为完整井。
(2) 双栓塞封隔的每一个试验段都位于潜水含水层之中,其厚度为试验段长度,记为L。
(3) 双栓塞封隔后每一个试验段为均质各向同性多孔介质,不同试验段多孔介质渗透系数各异。
(4) 裂隙含水层天然水力坡度为0,且侧向无限延伸。
(5) 测试井的水位变化为线性反应,不考虑井管中的摩擦效应,且测试井内外的压力水头瞬间平衡。
1.2 Bouwer & Rice数学模型的基本原理
Bouwer和Rice在通过大量现场Slug试验后发现井内水位迅速变化后水位恢复速率与时间成指数关系,并建立了均质非承压含水层Slug试验理论模型[3]。根据概化后的物理模型,考虑模型的适用性,采用Bouwer & Rice数学模型进行求解,其适用条件是:潜水含水层;均质各向同性多孔介质;定水头有限直径圆岛形边界条件;忽略含水介质的弹性储水效应。建立的Bouwer & Rice潜水井模型示意图见图2。

图2 Bouwer & Rice潜水井模型示意图Fig.2 Diagram of Bouwer & Rice model for well flow in unconfined aquifers 注:H(0)为激发强度(m)。
由于Slug试验对钻孔周围含水层的扰动较小,因而可以假设在Slug试验进行的整个过程中地下含水层水位保持不变,利用Bouwer和Rice给出的解析解推导过程如下[4]:
Slug试验中注入井中的水流运动过程满足变形后的Thiem公式:
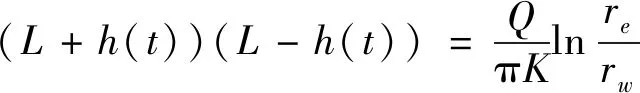
其中:
L+h(t)≈2L;
L-h(t)≈H(t)
可以得到模型的控制方程为
(1)
上式中:L为试验段滤管长度(m);h(t)为测试井中水位的位置水头(m);H(t)为测试井中水位的标准水头(m);K为含水层渗透系数(m/s);Q为含水层流量(m3/s);rw为滤管半径(m);re为Slug试验有效半径(m)。

(2)
将公式(1)代入公式(2)中,可得:
(3)
结合初始条件t=0时,H(t)=H(0)以及在t时刻H=H(t),可得到含水层径向渗透系数Kr的表达式为
(4)
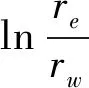
2 Slug试验过程概述
2.1 试验场区概况
试验场位于青岛董家口港区泊里某地下水封洞库内,场地地貌单元属波状剥蚀准平原,场地地形平坦,地势稍有起伏,地势总体上北高南低,场地目前处于施工阶段,大部分区域经过场平比较平整。根据水文地质调查及勘探成果,研究区主要地层岩性为燕山晚期青台山二长花岗岩,第四系覆盖层较薄,厚度范围为0.5~2.7 m。研究区内地下水的主要赋存类型为松散岩类孔隙水、碎屑岩类孔隙裂隙水。其中,松散岩类孔隙水赋存于场地第四系地层中,地下水以水平向渗流运动为主,部分垂直入渗补给下部裂隙水,相对于下部裂隙水而言,其富水性好,地下水水位埋深一般在0.00~3.40 m,地下水水位大多在该带随季节性变动,是地下水径流最活跃的部位;碎屑岩类裂隙水赋存于第四系地层以下,即燕山晚期青台山二长花岗岩中风化带中深部及其以下的岩体中,见图3。
2.2 试验方法
本次试验采用双栓塞多强度分段Slug试验,每段试验段长度为10 m,连接管半径为21 mm,滤管半径为44.5 mm。试验选择场地内VBH09号和VBH10号钻孔,表1列出了试验钻孔的基本信息。试验设备为武汉力博物探有限公司研发的钻孔智能压水测试仪,该仪器能自动监测、实时显示Slug试验全过程的地表压力和注水平均流量,数据灵敏度高、精确可信。试验开始前需测量钻孔天然地下水水位,按照设计试验段长度连接双栓塞,下放试验设备前在地表检测双栓塞密封性并确保各仪器能正常工作,检查无误后将试验设备下放至设计深度;试验设备下放后静置10 min左右,实时监测地下水水位,待水位稳定后给双栓塞加压,观测栓塞压力表读数是否稳定,待加压结束后静置数分钟,若栓塞压力值保持稳定即可开展Slug试验。试验过程中观测流量历时变化。
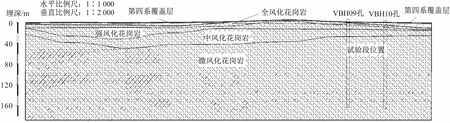
图3 试验场水文地质剖面简图Fig.3 Diagram of the hydrogeological profile of the test site

表1 试验钻孔的基本信息表Table 1 Basic information table of the test boreholes
Slug试验要求在天然静止水位条件下,瞬时激发钻孔内水位(激发时间一般控制在5 s内)。本次Slug试验采用瞬时注水的方式激发水位,通过调节离心泵功率控制激发时间,考察瞬时注水后水位回落情况。试验时先打开压水离心泵,激发3~5 s,之后迅速停泵,关闭进水阀门,压力传感器自动进行采集各段压力数据。其中,在VBH09号钻孔埋深为40~50 m试验段的激发强度(即激发水头)H(0)分别为1.9 m、7.1 m和19.0 m,埋深为50~60 m试验段的激发强度H(0)分别为1.0 m、6.7 m和19.0 m;在VBH10号钻孔埋深为41~51 m试验段的激发强度H(0)分别为2.9 m、10.2 m和17.0 m,埋深为51~61 m试验段的激发强度H(0)分别为2.0 m、9.8 m和20.0 m。Slug试验所获得的H(t)-t曲线,见图4。
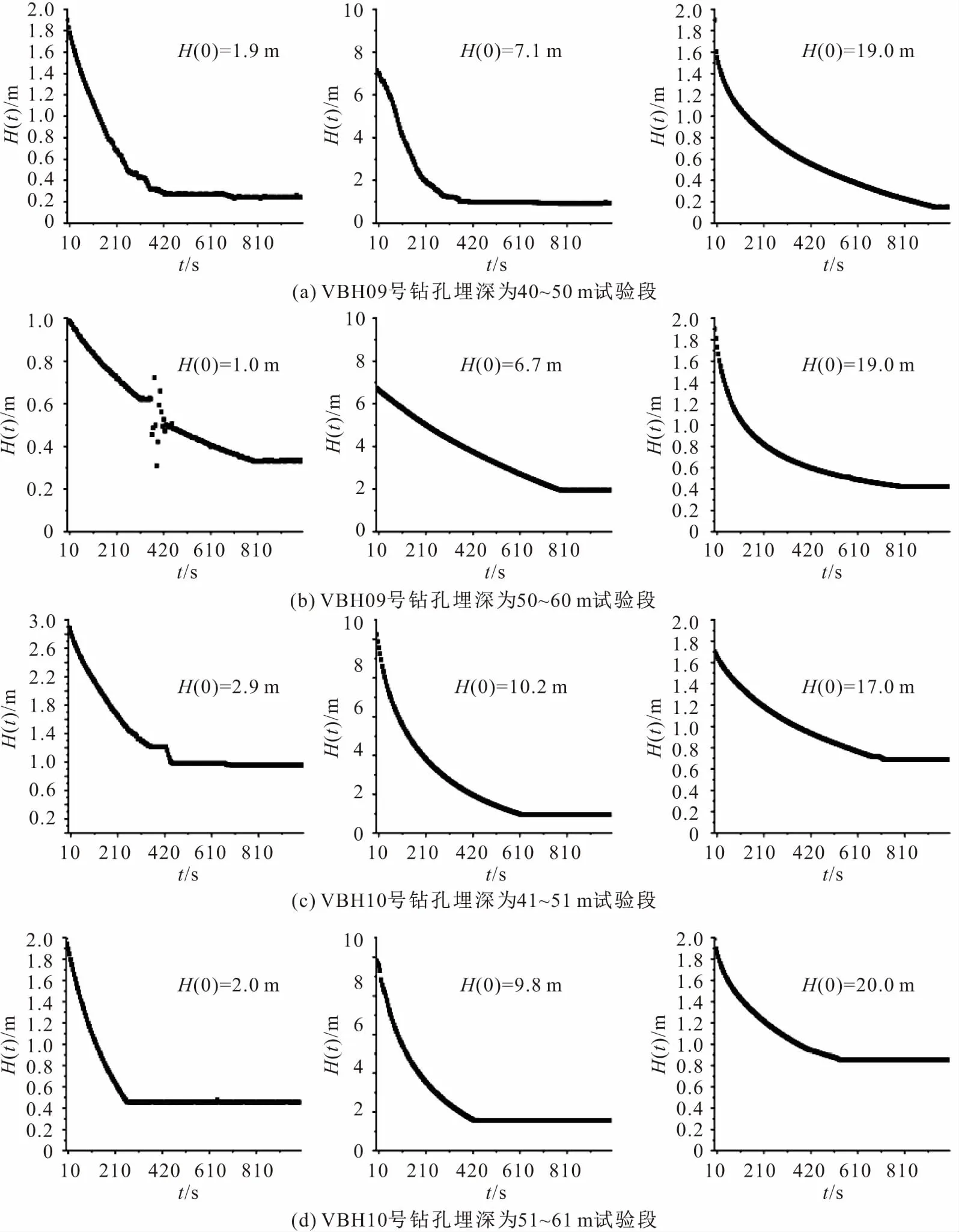
图4 Slug试验H(t)-t曲线图Fig.4 H(t) to t curves from the Slug test
由图4可见,所有Slug试验H(t)-t曲线均为指数恢复形态,试验为非线性振荡反应,适合采用Bouwer & Rice模型求解(注:VBH09号钻孔激发强度为1.0 m时Slug试验中期出现线性振荡反应,由于线性振荡反应历时较短,整体仍按照非线性振荡反应处理)。
为了便于对比不同激发强度下水位恢复情况,本试验激发强度H(0)选择水头稳定下降阶段t=0时刻的水头减去激发前实测静水位作为初始激发水头。由于试验设备所限制,水头只是理论上瞬时激发,且试验段地层渗透性较低。在裂隙岩体中开展Slug试验时,试验段水位恢复速率缓慢,一般试验历时无法使水位完全恢复,因此在低渗透性裂隙介质中开展Slug试验时,前期水位恢复比较明显,后期水位恢复十分缓慢,故本试验数据解析采用前期水位恢复较为明显的数据进行拟合。将实测水位数据与钻孔结构性参数代入公式(4)后,可计算得到试验段地层的渗透系数K值,见表2。
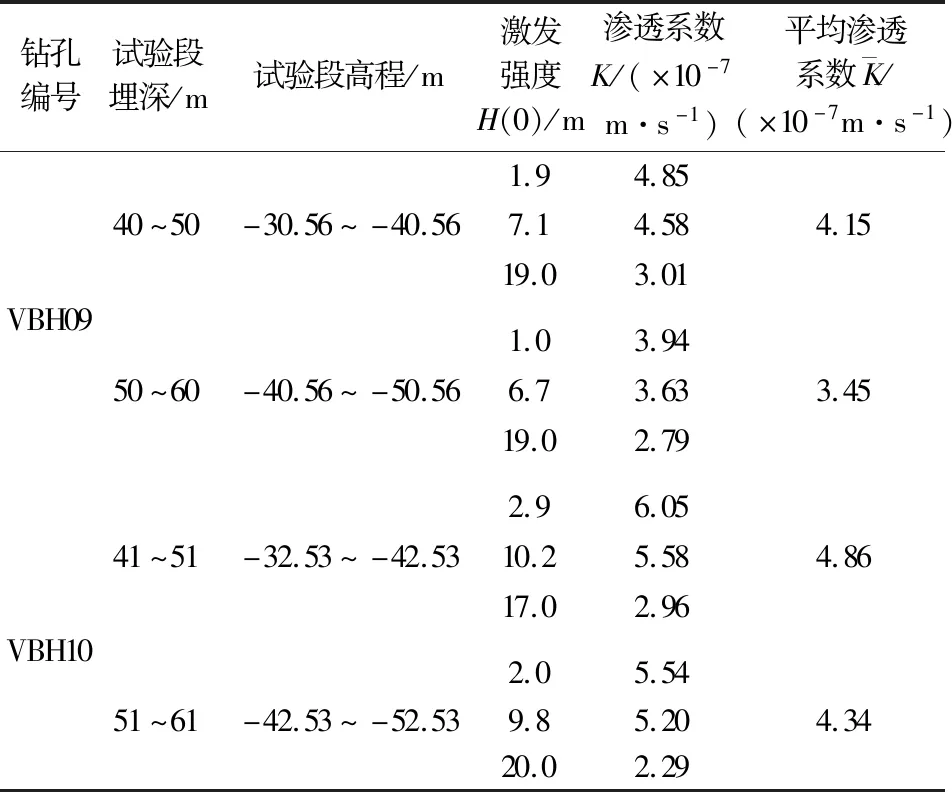
表2 Bouwer & Rice模型计算得到的试验段地层渗透系数K值Table 2 Results table of the stratum hydraulic conductivity K values of the test section by Bouwer & Rice model
3 Slug试验数据分析
3.1 试验段地层渗透系数K值的计算分析
根据表2可知,利用Bouwer & Rice模型计算得到的不同激发方式下试验段地层渗透系数K值有所差异,且激发强度H(0)与K值有很强的相关性,具体表现为K值随着激发强度的增加而变小(见图5)。其主要原因是当前Slug试验理论模型大多假设试验过程中地下水流动是基于达西定律的线性流动,由于达西定律表示压力损失完全由黏滞力决定,而Slug试验过程中实际地下水在低渗透裂隙介质中渗流时的压力损失不完全表现为黏滞力,因此不服从达西定律。在Slug试验中,如果激发水头过大势必导致地下水实际流速较高,地下水出现非线性流动,此时水力梯度与进出地层的流量不呈线性关系,故Slug试验解析数据的代表性和准确性都需要做进一步的分析。
3.2 对于非线性流的识别
雷诺数Re是研究地下水流态的重要物理量,其物理意义定义为惯性力与黏滞力之比。地下水在裂隙岩体中的渗流情况较为复杂,为了确定在Slug试验水位恢复过程中,地层单裂隙中是否发生过非达西流渗流,可定义代表性雷诺数为[18]
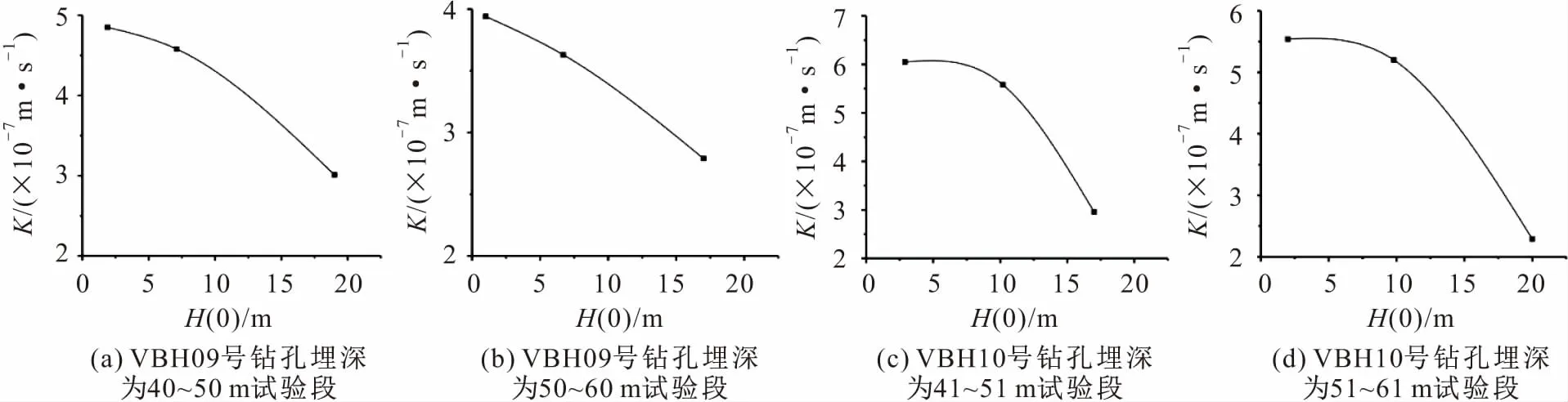
图5 VBH09和VBH10号钻孔不同埋深试验段激发强度H(0)与地层渗透系数K值的关系图Fig.5 Relationship between excitation intensity H(0) and stratum hydraulic conductivity K value of the test sections with various buried depths at the boreholes VBH09 and VBH10
(5)
式中:ρ为地下水密度(kg/m3);v为地下水流速(m/s);e为水力半径(m);μ为地下水动力黏滞系数( Pa·s);Q为地下水流量(m3/s);w为垂直于裂隙流动方向的隙宽(m)。
达西定律是在较为理想的试验条件下获得的。学者们通过对不同粒径的介质开展渗流试验,发现只有雷诺数Re在1~10之间的层流运动才符合达西定律,超过此范围,地下水渗流中渗透流速和水力梯度不再满足线性关系[15]。采用单裂隙模型进行的室内试验结果表明:当代表性雷诺数Re大于1~10时,非达西流现象是显著的。考虑到花岗岩基质的渗透率较低,假设在Slug试验中,地下水只通过开放的裂隙流入或流出地层,地下水沿径向流动,在井壁处流速最大,随着距离井壁距离的增加,地下水流速减小,故假设井壁附近最大地下水流速为v。为了计算Slug试验中试验段裂隙的代表性雷诺数,将平均地下水流量Qm和平均裂隙宽度wm定义如下[18]:
(6)
(7)
式中:Qm为平均地下水流量(m3/s);wm为平均裂隙宽度(m);Qi为第i条裂隙的地下水流量(m3/s);θi为第i条裂隙的倾角(°);Nf为试验段内裂隙数。
公式(6)中的试验段裂隙岩体中地下水总流量可由下式给出:
(8)

为了对Slug试验过程中地下水流态进行识别,需结合试验段内裂隙的位置、长度、宽度及走向等地球物理测井数据求取代表性雷诺数。试验过程中真实的雷诺数可能比计算的代表性雷诺数要大,这是合理的,因为采用代表性雷诺数方程计算值是某一时间段内雷诺数的平均值。VBH09号钻孔和VBH10号钻孔不同埋深试验段在不同激发强度下代表性雷诺数的变化,见图6。
由图6可见,瞬时改变Slug试验测试段内水位后,在水位恢复初期代表性雷诺数(Re)达到最大值并随水位恢复过程Re逐渐下降直至为零(注:VBH09号钻孔激发强度为1.0 m时试验中期出现非线性振荡反应且所求得的Re较大,由于非线性振荡反应历时较短,此时非线性振荡反应所求得的Re并未展现在图中)。Ji等[18]研究发现,对于裂隙花岗岩含水层,代表性雷诺数Re达到1时,试验段内地下水会出现非线性流动,并定义了平均雷诺数Rec,其是指整个Slug试验水位恢复过程中的整体代表性雷诺数,而在Slug试验中,如果激发强度过大则诱发地下水实际流速较高,这会导致试验初期钻孔周围含水层中地下水出现非线性流动,此时水头梯度与进出地层的流速不是线性相关的,这时采用Slug试验求取的地层渗透系数值偏低。通过计算试验段内的代表性雷诺数Re随时间的变化,可识别出Slug试验水位恢复过程中试验段内地下水随时间的代表性流动状态。由此可以发现,无论初始激发强度的大小如何,代表性雷诺数Re随时间的变化趋势是相似的,即Re在测试开始时达到最大值,并且随时间下降直至为零,这表明对于含多条裂隙的介质,当平均雷诺数Rec相对较小时,非达西流是可能存在的。图7显示了在两个钻孔开展不同初始激发强度的Slug试验水位恢复过程中平均雷诺数Rec的变化趋势。

图6 VBH09和VBH10号钻孔不同埋深试验段在不同激发强度下代表性雷诺数Re的变化图Fig.6 Change of the representative Reynolds number of the test sections under various buried depths at boreholes VBH09 and VBH10 with different excitation intensity
由图7可见,平均雷诺数Rec随初始激发强度H(0)的增加而增加,且随着H(0)的增加Rec增加速率有所降低。

图7 VBH09和VBH10号钻孔在Slug试验水位恢复过程中平均雷诺数Rec与激发强度H(0)的关系图Fig.7 Relationship curve of average Reynolds number Rec and excitation strength H(0) in the water level recovery process of Slug test in the two boreholes
3.3 临界激发强度的分析
为了避免Slug试验过程中非线性流对试验结果的干扰,保证试验段地层渗透系数值的精准性,从而为今后Slug试验在实际工程勘察中的应用提供借鉴和参考,需要确定因激发水头导致的线性流与非线性流之间的临界激发强度。结合公式(5)~(8),可得出平均雷诺数Rec的计算公式为
(9)
式中:T为水位恢复过程中雷诺数下降为0时所需的时间(s);H0为临界激发强度(m);其他符号意义同上。
根据Ji等[18]的研究,对于裂隙花岗岩含水层,当平均雷诺数Rec达到3时,非达西流效应比较明显。为了对Slug试验过程中激发强度过大而导致的非线性流进行识别,推导出临界激发强度H0的计算公式为
(10)
该公式可结合地球物理测井资料和水位恢复资料求取,且求取方便。在实际工程中,可根据地质资料预先选择一个适中的激发强度开展Slug试验,若此激发强度满足公式(10),可认为此激发强度下地下水非线性流对地层渗透系数值求取结果的影响较小,已选激发强度适用于在该地区开展Slug试验;若不满足公式(10),可将激发强度适度降低并继续开展Slug试验,直至所选用的激发强度满足临界激发强度计算公式。
4 结论与建议
(1) 为了识别Slug试验水位恢复试验过程中地下水的非线性流动行为并讨论分析临界激发强度,通过开展多深度多强度Slug试验,计算了VBH09号和VBH10号钻孔不同埋深试验段不同激发强度下的地层渗透系数,并利用地球物理测井数据计算试验段代表性雷诺数Re和平均雷诺数Rec,推导出临界激发强度H0的计算公式,并对野外Slug试验激发强度的现场选取提出了方案,可为今后有关的勘察工程提供参考。
(2) Slug试验结果表明:在本研究区开展Slug试验,当激发强度较大时,会导致试验过程初期试验段内实际地下水流速较高,从而出现非线性流动,进而对试验结果造成影响;随着激发强度的增加,受非线性流的影响,采用常规Slug试验,理论模型求取的地层渗透系数估计值有降低趋势。因此,在实际工程应用中,需要将地球物理测井数据与Slug试验结果相结合,共同求取水文地质参数,以保证参数求取结果的准确性。
(3) Slug试验受钻孔温度效应、井筒储存效应、孔壁皮肤效应的影响较大,而裂隙网络渗流特性和物质运移特性的影响因素较为复杂,本文在运用Slug试验解析模型时对上述因素的影响考虑不够全面,后续的研究可建立进一步考虑上述效应的Slug试验渗流模型,以提高Slug试验解析数据的精确性。

