基因表达式算法的民航涡扇发动机可调放气阀门工作基线建模

(中国民航飞行学院 航空发动机维修培训中心，四川 广汉 618307)

0 引言

对于航空发动机来讲，压气机的喘振会导致强烈的机械振动和热端超温，在极短的时间内就可能会造成发动机部件的严重损坏。现役的民航涡扇发动机多采用可调放气阀门(variable bleed valve, VBV)放出部分压气机空气以达到防喘的目的，所以可调放气阀门的工作状态对飞行安全的影响很大。相关研究结果表明，在飞机起飞和巡航段，如果VBV阀门的开度过大，有可能导致飞机飞行推力下降超过10%，引起飞机发动机推力失控事件的重大事件；在巡航和慢车速状态时，如果VBV阀门开度过小，易引起发动机的增压机喘振故障；在起飞、巡航和慢车状态中，如果VBV阀门开度振荡不定，会导致发动机推力下降超过10%，并且易发生喘振故障现象。因此研究可调放气活门对于发动机监控，从而及时发现不良变化预防飞行事故具有重大的意义。

另一方面，随着我国航空事业的发展，航空发动机已不再依赖统一定期以及事故后的维修方式，而是转变到根据每一架航空飞机的实时状态来定点视情维修。而这种更为精确的维修方式，要求对飞机每一个部件工作参数是否正常地了解，可以以较少的经济时间成本换取更可靠的飞行过程。然而国内所用的民用涡扇发动机基本全部由国外公司生产，其部件特性、结构参数与控制特性等均无从得知，因此无法建立对发动机进行视情监控和故障诊断的数学模型[1]。

近年来，我国航空公司开始利用飞机快速存储记录器数据(QAR)数据实施飞机性能监控。QAR数据包括用于飞行状态性能判断的各个设备实时温度、阀门开度、飞行速度、旋转速度等100多个参数。同时，QAR译后数据库还有其他功能，包括飞行航迹和飞行剖面的图形化查看以及飞行数据导出为Excel文件等。因此可以通过对QAR数据的挖掘，即利用系统的输入输出参数对发动机的系统进行辨识，构造一个相对真实的反映对象的数学模型[1]。

本文即是根据QAR数据中的参数来辨识航空发动机阀门VBV的数学模型，也称工作基线，即处于良好工作状态的发动机在标准状态下VBV与其控制参数之间的函数关系。VBV的控制参数较多，定性工作基线模型为：

VBV=f(N1K12, N2K25, VSV, TAT, T2.5, TLA, N1 ACT, P0)

其中：

N1K12为低压转子修正转速与额定转速的百分比(%)；

N2K25为高压转子修正转速与额定转速的百分比(%)；

VSV为可变静子叶片的角度(°)；

TAT外界大气温度(℃)；

T2.5为高压压气机进口温度(℃)；

TLA为油门杆角度(°)；

N1为低压转子实际转速与额定转速的百分比(%)；

P0为外界大气静压(PSIA)。

根据CFM56-7B发动机生产厂商CFM公司的文献[2]，综合考虑影响VBV开度的各种因素，排除的次要参数，最终将CFM56-7B发动机的VBV的定性工作基线模型简化为：

VBV=f(N1K12, N2K25,VSV ,TAT, T2.5)

本文辨识过程中所有参数样本均来源于实际的QAR数据。选择了一架BOEING737-800飞机左右两台发动机(这两台发动机CFM56-7B的装机时间均为2015年5月，CSN均为4 200)，收集了他们在2018年1月共25个航班，共50组QAR解码以后的数据。每次航班的数据由于飞行时间的不同，共有7 500到12 000条数据不等。在使用时依据了以下的原则预先对数据进行筛选[3]。

1)选用发动机循环数较少的数据；

2)选用发动机性能良好的数据；

3)剔除有显著差异的数据。

除此之外，为了排除数据单位对最终结果的影响，对所有数据进行了归一化处理。为了简化计算，数据量进行了4倍压缩。最终，所用的数据经过了筛选、剔出和压缩等预处理操作，保证了数据的可靠和统一。

1 航空发动机阀门VBV工作基线系统辨识的常规方法

早在60年前，国外就开展了飞机工作性能与故障性诊断结合起来统一研究。我国30年前，也开始了同样的工作。比如，我国中国民航学院的林兆福教授就提出，可以应用正交实验设计原理及最小二乘法曲线拟合原理来建立航空发动机工作基线[4]。哈尔滨工业大学的钟诗胜教授又进一步提出，利用多元非线性回归的方式，采用高斯牛顿迭代法对多元非线性回归方程进行回归分析[5]。再之后，中国民航大学的曹慧玲教授采用支持向量机回归算法，开始用厂家监控系统数据和飞机快速存储记录器数据两种方式对基线进行挖掘分析[6]。

对于航空发动机这样的复杂非线性系统，要对其进行系统辨识是比较困难的事情。针对这样的非线性模型，可使用的先进辨识算法有以下几类，分别介绍如下。

1.1 Volterra泛函级数

Volterra泛函级数具有鲜明的物理意义，切合非线性动力学的工程系统。但这种方法需要相当高的参数才能保证辨识结果的精度，计算比较困难。

1.2 NARMAX

NARMAX 模型即带外生变量的非线性自回归滑动平均模型。这种方法在实际中，可将给定的模型辨识问题简化为最小二乘估计问题，因此得到较为广泛的应用。但缺点是最近模型的精度取决于正确的模型结构。

1.3 ANN

人工神经网络算法(ANN)具有逼近任意非线性函数的能力。但训练算法、网络类型等需要实行指定，比较依赖先验知识，结果也不能提供简洁显性的知识表达。

1.4 模糊逻辑

模糊逻辑算法理论上可以以任意精度逼近任意一个定义在致密集上的非线性函数。但实际还有考虑算法的可操作性和模型的可解释性。

1.5 VSM

支持向量机VSM和人工神经网络一样，是一种新兴的通用学习工具，具有强大的非线性逼近能力。可以在有限样本的情况下，得到现有信息的最优解。但VSM得到的模型不能提供明确的数学表达式，难以分析系统的动稳态性能。

1.6 遗传算法

常规的遗传(GA)算法不需要先验知识，可以并行计算，全局寻优。可以快速高效地解决复杂高维和高非线性问题，具有非常突出的优点。后来GA算法发展出遗传编程(GP)算法，可以自动生成程序来解决问题。使用GP算法进行系统辨识，不需要对模型结构进行任何假设，可以在多目标下自动寻找适合的模型结构，同时优化模型结构和参数。

在GA和GP算法基础上，进一步发展了基因表达式编程(GEP)算法。这是一种基于生物基因结构和功能发明的一种新型自适应演化算法。具有GA和GP算法的优点，编码方式较为简单，易于进行遗传修饰的操作，并且具有结构和功能上的多样性。由于GEP在解决复杂的函数发现等问题上具有较好的性能，故在科学计算和商业应用等领域取得了广泛的应用[7]。

由于飞机发动机可调放气阀门VBV工作基线是一个多维，强非线性的复杂曲线。采用前面5种系统辨识方法，会遇到缺乏先验知识，数据量大，容易陷入局部最优，不能生成确定的数学表达式等种种问题。相比其他算法，GEP算法具有以下优点[8]。

1)具有强大的表达复杂问题的能力和快速高效的搜索能力，辨识结果不易陷入局部最优解。

2)不依赖于先验知识，可以自动搜索所有可能的非线性模型空间。

3)能够产生任意复杂度的模型结构，发现具有最优性能的动态表达式。

4)还可以进行多目标进化，使目标模型可以在复杂度和精确度之间实现平衡。

因此本文采用GEP算法来解决飞机发动机可调放气阀门VBV工作基线系统辨识这一问题。

2 VBV工作基线系统辨识的GEP算法设计

基因表达式编程的算法流程如图1所示。首先，随机产生一定数量的染色体个体(初始种群)，然后，依据待解决的问题要求，计算个体的适应度。然后按照个体适应度进行选择，选中的个体进行有修饰的复制，留下具有新特性的后代。接下来，这些新的个体也要经历相同的发展过程：基因组的表达，计算适应度，选择和有修饰的复制，该过程重复若干代，直到发现一个优良解[9]。

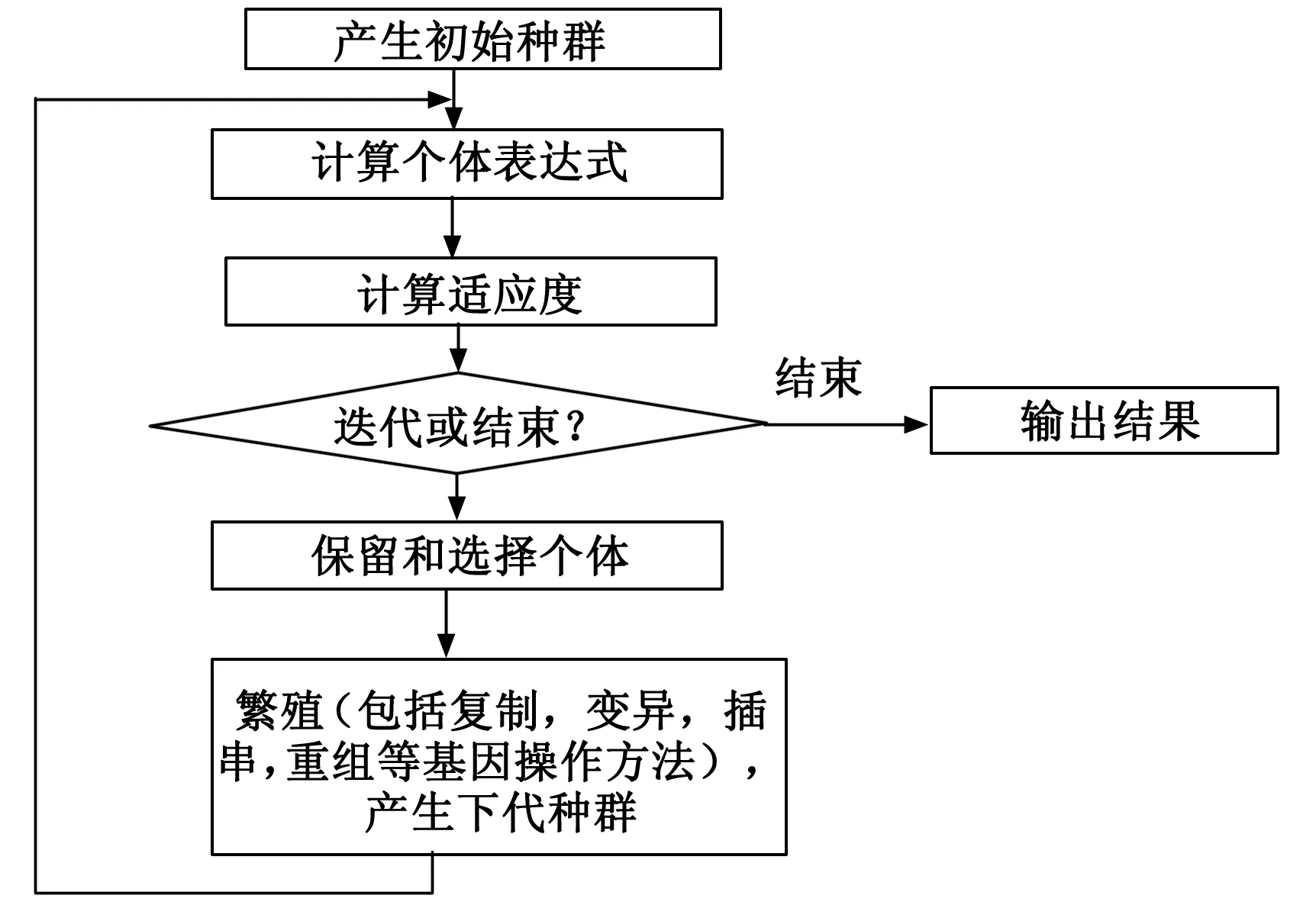
图1 GEP算法流程

将GEP算法用于工作基线函数挖掘具体工作，就是将5个VBV控制参数和可能的函数关系构造到初始染色体中，编码形成表达式树，计算表达式对应的适应度，选择适应度最好的染色体进行变异、插串、根插串、单点重组、两点重组、基因重组等操作，使染色体不断改变，越来越适应VBV数据所呈现的规律，直到最终匹配。适应度最高的染色体对应的表达式就是工作基线函数。

在对工作基线函数GEP算法编程中，所使用的开发软件是Matlab语言。这是美国Mathworks公司开发的高级技术计算语言和交互环境，广泛用于算法开发、数据可视化、数据分析和数值计算中。算法中具体设置如表1所示[10]。

表1 VBV工作基线函数挖掘中GEP算法相关设置

算法中适应度的判别采用残差平方和SSE，即拟合数据和原始数据对应点的误差平方和。计算公式如下：

当SSE的值越接近0，说明拟合数据越接近于原始数据，模型的预测越成功，拟合度越高。以SSE为适应度进行判别，可以让进化过程朝着拟合优度越来越大的方向进化。以一组数据进行迭代计算的适应度变化曲线如图2所示。

图2 适应度变化曲线

当程序迭代到300代，适应度达到0.98，此时拟合出运行曲线如图3(a)所示。将拟合出的曲线图3(a)和QAR中实际测出的曲线图3(b)对比，可以看出曲线的形状基本一致，仅在少部分地方有些出入。图3(c)进一步给出了拟合曲线和实测曲线之间的误差曲线，可以看出误差量很小，基本接近于零。说明GEP算法辨识VBV工作基线，误差小精度高，高效可靠。

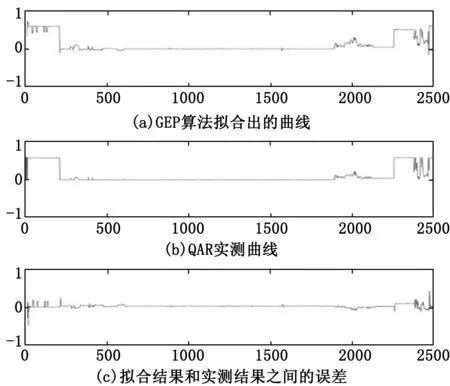
图3 QAR实测曲线，GEP算法拟合曲线及两者误差

3 VBV工作基线函数曲线拟合结果分析

图3的结果是GEP算法针对一个航班一台发动机的压缩数据，经过300代的迭代计算后，挖掘出的可调放气活门的开度VBV的工作规律。该规律经过表达式译码，写成公式为：

VBV=F(a,b,c,d,e)=0.2957+4Δ(d)+

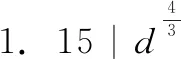
0.0049c+0.0047e

其中：a,b,c,d,e分别代表低压转子修正转速与额定转速的百分比N1K，高压转子修正转速与额定转速的百分比N2K，外界大气温度TAT，可变静子叶片的角度VSV，高压压气机进口温度T2.5这5个控制参数。

从上述拟合公式可以看出，可调放气活门的开度VBV与可变静子叶片的角度VSV关系最为密切，公式中2、3、4项都和VSV直接有关，对VBV最终数值其决定性的作用。说明VBV主要受VSV数据的影响。

另外，从公式可以看出，可调放气活门的开度VBV除了受可变静子叶片的角度VSV的影响外，同时也受低压转子修正转速与额定转速的百分比N1K，高压转子修正转速与额定转速的百分比N2K，外界大气温度TAT，高压压气机进口温度T2.5四个参数的影响，但影响相对较小。在这4个因素中，低压转子修正转速与额定转速的百分比N1K相对其它因素影响更大，在公式中第4、6项均和N1K有关。而高压转子修正转速与额定转速的百分比N2K，外界大气温度TAT，高压压气机进口温度T2.5这几项和最终可调放气活门的开度VBV有一定的关系，但整体影响较小。这些规律和实际中的直观影响相符，说明上述由GEP算法拟合出来的基线方程是贴合工程实际的。

但是该基线方程是由一次航班的一个发动机数据拟合出来的。为了深入讨论拟合结果的普遍性，将基线方程应用到其它航班数据中进行验证，验证时采用了以下指标：

确定系数(R2)：

其中：

确定系数R2越接近于1时，说明该拟合模型的拟合优度越高。由于确定系数会随着模型自变量数目增加而增加，为了让最终效果更精确，对确定系数进行修正，进一步采用修正确定系数adjustedR2。

修正决定系数(adjustedR2):

残差平方和(SSE)：

残差平方和(SSE)越小，拟合结果与实测数据之间的误差越小，说明拟合结果越准确。

均方误差(MSE)：

均方根误差(RMSE)：

均方误差(MSE)、均方根误差(RMSE)和残差平方和(SSE)一样，用来反映所得的拟合模型数据和实际数据之间的差异程度，数值越小说明两者越接近。

使用前面GEP算法拟合出来的模型公式，对随机选取的两次航班不同日期共50组的发动机数据进行检验。分别计算了确定系数(R2)、修正决定系数(adjustedR2)、残差平方和(SSE)、均方误差(MSE)、均方根误差(RMSE)，其结果如表2所示。

由表2中结果可知，50组数据利用函数模型进行验证所得到的结果相差不大，说明拟合函数总体可靠。确定系数(R2)和修正决定系数(adjustedR2)除去唯一一个数据以外，其余均高于0.95以上，说明函数的拟合优度好，拟合数据对实测数据的解释程度高；均方误差(MSE)在0.010 2～0.023 0之间，平均0.014 8；均方根误差(RMSE)在0.105 0～0.144 3之间，平均0.120 8，表明拟合函数数据分散在实际曲线附近，离散度很小，与实际曲线契合程度非常高。

4 结束语

通过对民航涡扇发动机QAR数据的挖掘，利用GEP算法找到了一个相对真实的民航涡扇发动机可调放气阀门(VBV)的工作基线数学函数。验证结果表明，GEP算法挖掘得到的结果精度高，误差小，在有限样本条件下对于民航涡扇发动机VBV工作基线的非线性建模具有很高的准确性，所构建的模型可以满足民航对可调放气活门进行监控和故障诊断的需要。

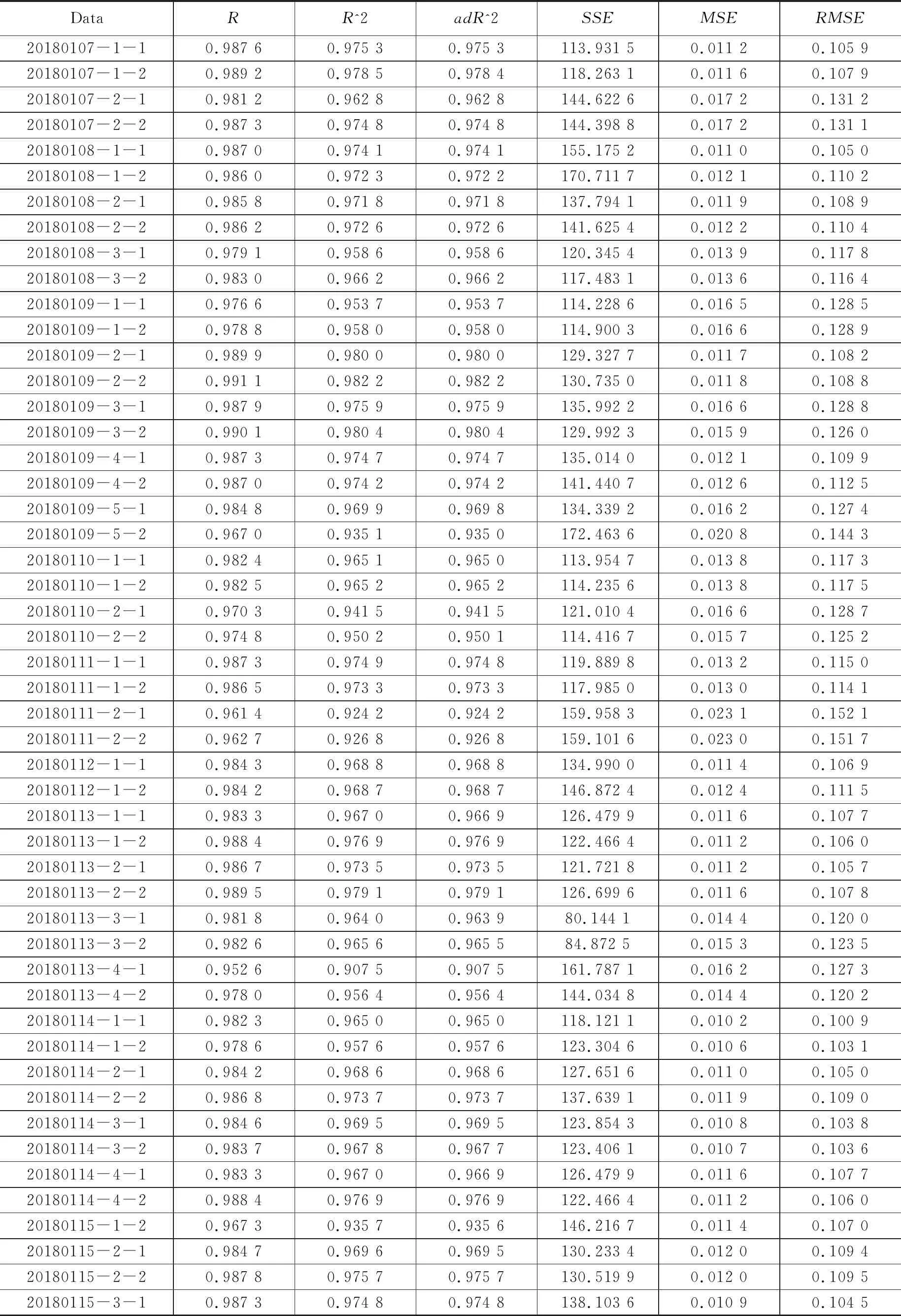
表1 GEP算法拟合模型对随机选取发动机数据组检验结果