数学课堂中“问题”设计的几点思考

夏彬

摘 要：数学是一门基础学科，它的内容深，知识点密集，知识间的联系比较紧密，要想在有限的课堂教学时间内取得较好的教学效果，在课堂教学中合理设计好问题是至关重要的。课堂提问不仅可以让学生巩固知识，反馈学情，培养学生的分析能力和钻研创新能力，也能使学生减少接受和理解知识的困难，同时也发展了学生的逻辑思维能力，语言表达能力和交流能力。以下就数学课堂教学中的问题设计谈几点设想。

关键词：数学课堂;“问题”设计;思考

回答老师提出的“问题”是课堂中学生获取知识的一种方式，问题的好坏直接影响了学生的学习效果。在数学课堂上，老师们会围绕本节课的知识点提出很多问题，但是有些时候课堂容易变成一些问题的简单堆砌，而且有的问题本身还过于枯燥，难以激发学生兴趣;有的离开教学重点，偏难偏怪;有的只注重均衡水平，缺乏层次性等等。因此对于问题的设计，笔者有一下几点思考：

一、问题的设计要契合学生的认知水平

《新课程标准》的倡导核心就是教学要以学生为主体，因此我们在设计问题时就要站在学生的认知程度上，这就要求教师能设计出符合学生认知发展规律的问题，同时这些问题需要具有一定坡度，往往从容易被学生接受的问题出发。比如，在教授《三角函数》这章内容的时候，我们如果一上来就提出“大家讨论一下正弦函数的图像是怎样的？”这个问题，虽然可能部分预习过的同学凭记忆能画出它的大致图像，但是这样的问题显然是不符合学生当时的认知水平的。而如果我们在演示完正弦函数的图像是如何得到的之后，再让学生对于余弦函数的图像进行分组讨论，在教师的帮助和引导下，学生再回答出这个问题，或许比之前的做法更有意义，学生也能获得一定的成就感。

二、问题的设计最好有现实意义

我认为最初可以从我们高中数学的应用型章节和内容着手，如1、函数，在日常生活普遍存在的求利润最大、时间最短、用料最省等问题;2、三角，诸如测量、建筑、航行等与三角函数知识有关的实际问题;3、数列，社会现实生活中人口增长问题、人寿保险问题，经济活动中存款利息、分期付款、期货贸易和生产活动中的资产折旧、增长率等与时间有关的实际问题;4、不等式，实际应用的投资决策、环境保护、生产规划、统筹安排、交通运输、最优化等问题及有关最大（小）值的实际问题;5、立体几何，现实生活中，诸如材料加工涉及几何图形的几何特征的应用题;6、解析几何，现实世界中诸如航行、天体运行的应用问题。7、排列组合，现实生活中存在着许多与人和事物的排列顺序、组合的种类有关的应用问题。这些问题由于其与生活的紧密联系，比较容易引起学生参与讨论的热情，能最大范围的调动学生的积极性。

三、问题的设计最好具有一定的开放性

一个开放性的问题更容易激发学生的想象力，培养学生的创新力。问题的开放，也就意味着有不同答案，这些答案或许可以反映不同层次的思维能力，从另一方面说，也能让不同思维层次的学生都参与其中。

比如在《集合的运算》的教学中可以引用下面这个问题，

例、若四面体各棱长为1或2，且该四面体不是正四面体，求该四面体的体积。

本题的答案是不唯一的，学生在交流的时候，不但可以表达自己的答案，更能从别人的答案中获得收获，这也恰恰体现了课堂学习的重要意义。

四、问题的设计要服务于教学的重难点

课堂中教师提出的任何一个问题，都要有利于教学重难点的突破，来帮助学生更好地掌握知识、巩固技能。

比如在《函数关系的建立》的教学过程中可以引入下面的例题，

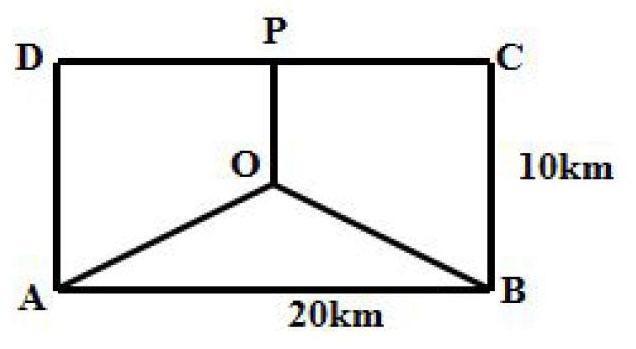
例、某地有三家工厂，分别位于矩形ABCD 的顶点A、B及CD的中点P处，已知AB=20km，CB=10km，为了处理三家工厂的污水，现要在矩形ABCD的区域上（含边界），且与A，B等距离的一点O处建造一个污水处理厂，并铺设排污管道AO，BO，OP，设排污管道的总长为Skm.

（一）满足条件的点O，可以取在哪里？

（二）为确定点O的位置，你可设什么为变量x？并根据你所设的x，建立S与x的函数关系式。

本节课的重难点是从一些简单的实际问题中建立两个变量间的函数关系式，并通过函数关系式的建立，培养学生把现实问题转化成数学问题的能力。同学们在回答这个问题的同时，既掌握了本节课的重点，也解决了函数关系建立的难点。

五、问题设计要有层次性

人的认识发展是渐进的，问题设计就要符合这个规律，往往是从简到难，简单的问题就好比是脚手架，可以是较难问题的一种简化，学生在解决简单问题的过程中掌握问题的本质，从而完成对较难问题的分析和求解。通过这些问题来培养学生的类比或者化归的能力。

比如，在学习“椭圆、双曲线、抛物线”这一章节后，教師可布置这样一个合作学习的问题：

（一）平面上到定点F1、F2的距离的和、差、积、商分别等于常数的动点的轨迹是什么？

（二）平面上到定点F1和定直线L的距离的和、差、积、商分别等于常数的动点的轨迹是什么？

（三）平面上到定点F1、F2的距离平方的和、差、积、商分别等于常数的动点的轨迹是什么？

通过这种问题链，让学生始终在自己的最近发展区学习不仅有利于培养学生的更好地解决问题，还能教会学生如何去探究问题，即从简单的出发，步步前进。套用华罗庚一句话，解决数学问题要学会退，退到不能再退位置。

当然，以上所列举的各条设计原则不可能在每一个问题中都得到充分的体现。但是笔者相信，只有遵循这样的原则，才能激发起学生自主探索的热情，更好地培养学生良好的数学素养。