借助GeoGebra 的3D作图功能认识空间解析几何中的平面与曲面
闫 湛,杨付贵
(广州工商学院,广州 510000)
1 GeoGebra软件简介
GeoGebra软件[1-2]诞生于2002年,是由美国佛罗里达州亚特兰大学的Markus Hohenwarter教授设计出的一款结合几何、代数、微积分和概率统计的免费动态数学软件。不同于需要编程的MATLAB软件,这款软件简单易学,作图快捷高效,可以利用滑动条在3D绘图区展示图形动态的形成过程。目前的最新版本是GeoGebra 6.0,美中不足的是新版软件导出中缺少了GeoGebra 5.0版本中的动画模式。
2 借助GeoGebra,认识空间解析几何中的平面和曲面[3-5]
2.1 借助GeoGebra,认识空间解析几何中的平面
高等数学(同济版)第8章第三节平面及其方程中提及到对于一些特殊的三元一次方程应该熟悉它们的图形特点,但只靠语言的描述无法提高学生的想象力,因此,对这部分的描述利用GeoGebra软件进行恰当举例绘制,用以辅助教学,加深学生对特殊情况的理解。
例如:对于平面的一般方程Ax+By+Cz+D=0
当A=0时,方程成为By+Cz+D=0,法向量n=(0,B,C)垂直于x轴,方程表示一个平行于(或包含)x轴的平面,不失一般性,在GeoGebra软件中拖动滑动条B、C、D使其值由-5变动到5,得到了如图1所示的效果图。同理,可在软件中观察Ax+Cz+D=0和Ax+By+D=0分别表示一个平行于(或包含)y轴和z轴的平面。

图1 平行于(或包含)x轴的平面Fig.1 Plane parallel to (or containing) the x-axis
当A=B=0时,方程成为Cz+D=0,法向量n=(0,0,C)同时垂直于x轴和y轴,方程表示一个平行于(或重合于)xOy面的平面,不失一般性,在GeoGebra软件中拖动滑动条C、D使其值由-5变动到5,得到了如图2所示的效果图。同理,可在软件中观察Ax+D=0和By+D=0分别表示一个平行于(或重合于)yOz面和xOz面的平面。
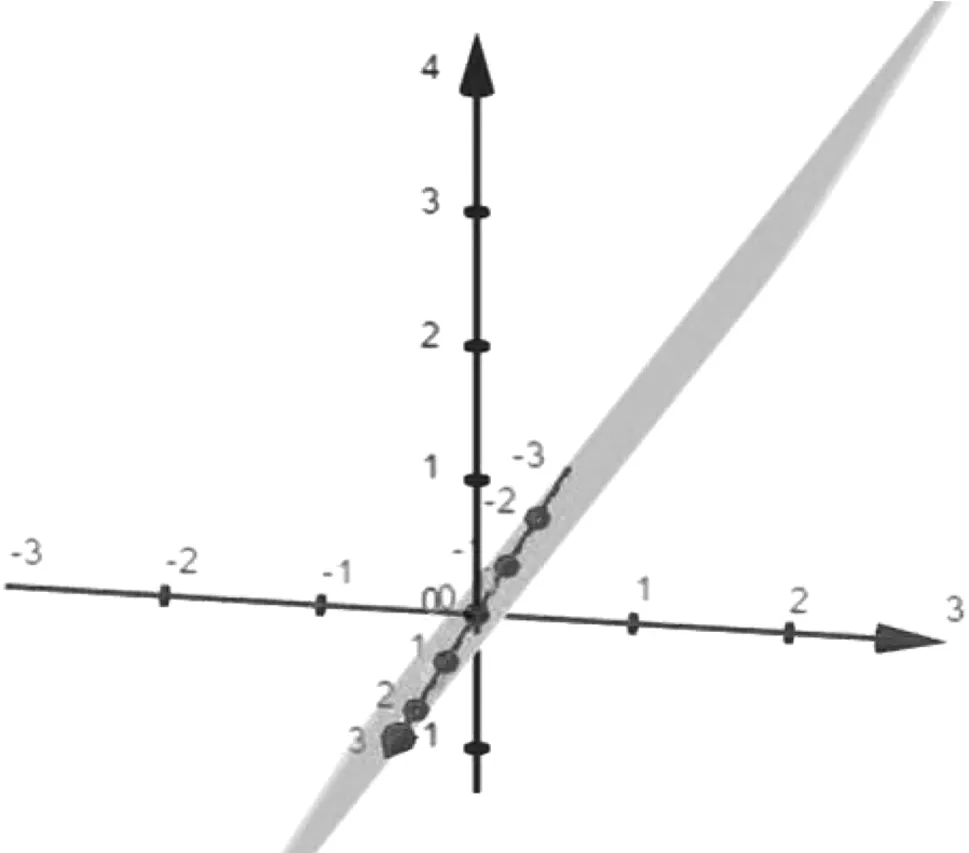
图2 z=ycotα平面Fig.2 Plane of z=ycotα
2.2 借助GeoGebra,认识空间解析几何中的曲面
2.2.1 借助GeoGebra,认识空间解析几何中的圆锥面
圆锥面是由直线L绕另一条与L相交的直线旋转一周所得的旋转曲面。若在GeoGebra软件中输入函数z=ycotα,当确定了α值时,就会在3D绘图区出现一个包含x轴的平面,如图3所示。
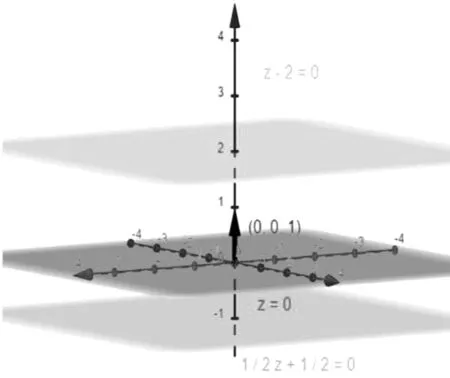
图3 平行于(或重合于)xoy面的平面Fig.3 Planes parallel to (or overlapping with) the xoy plane

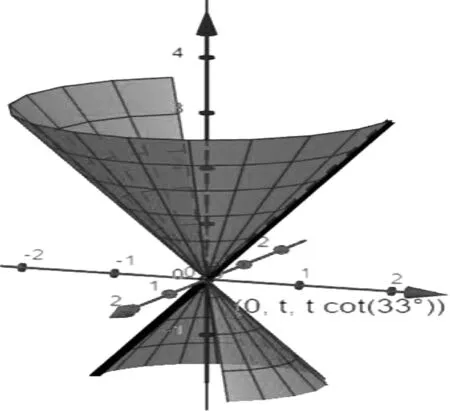
图4 圆锥面Fig.4 Conical surface

图5 z=ycotα直线Fig.5 Line ofz=ycotα
输入滑动条θ角度使空间中的直线能绕某一条直线转动一周构成旋转曲面,调出曲面命令:曲面(直线、旋转角度、旋转轴)即可得到如图5所示的效果图。
2.2.2 借助GeoGebra,认识空间解析几何中的抛物柱面


图6 抛物运动Fig.6 Parabolic motion
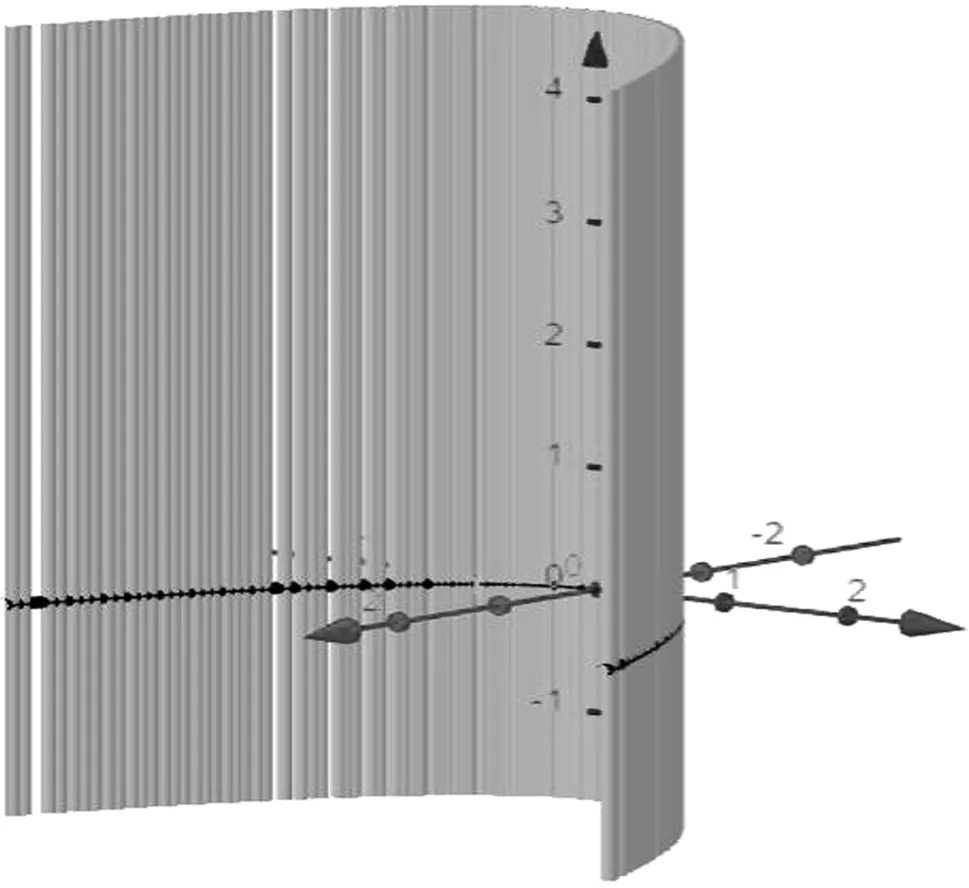
图7 抛物柱面Fig.7 Parabolic column face
当滑动条a从-5变动到5时,母线就可以沿着抛物线运动,得到的运动轨迹就是抛物柱面,效果图如图7所示。

