指向深度学习的高中物理教材整合与教学建议——以“匀变速直线运动的位移公式推导”为例

(江苏省沙溪高级中学,江苏 苏州 215400)

1 引言

深度学习倡导深度加工知识体系，深度理解概念规律，深度掌握知识内涵,进而实现深层次自主构建,达到提升学生的思维能力的目的，深度学习是以解决真实情景中的复杂问题为目标的有效学习。教材设计立足于学生获取相应的学科知识，发展学生思维和探究能力,培养学生的科学态度和责任感。物理教材设计的共性特征是取材于生活并指向生活,通过深层次的教材挖掘,学生除掌握基本的概念和规律外,更重要的是能够凝练出科学方法，以解决实际问题。然而学生的认知水平和思维层次很难处于同一水准,教材的设计往往力求受众面广,可能会影响教材的深度,限制学生思维层次的提高。全国各版本高中物理教材的设计尽管知识体系大体相同,但在设计思路和编排顺序等方面还是有较明显的差异。教师在教学前如果能认真研究各版本教材内容,分析差异，取长补短,适当进行整合编排,更有利于学生的知识掌握，进而指向深度学习。

2 多版本教材中“匀变速直线运动中位移公式推导”内容简析

2.1 人教版

人教版教材首先运用v-t图像研究了匀速直线运动的位移,说明v-t图像下的“面积”表示位移，在“思考与讨论”环节通过粗略估算小车运动的位移,引导学生得出时间间隔取得越短,估算越精确。最后从微元法的角度结合v-t图像,得出“面积”即位移的结论,最终推导出位移公式。

2.2 粤教版

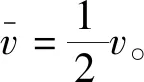
2.3 鲁科版

鲁科版教材的做法与粤教版教材类似,也是从速度公式和平均速度公式出发得出结论。但在本章的“拓展一步”中,教材从v-t图像出发,采用微元法,无限分割匀变速直线运动,得出v-t图像下的“面积”即为位移的结论。

2.4 沪科教版

2.5 教科版

在教科版教材第二章第六节中设置了“交流讨论”栏目,从匀速直线运动的位移入手,启发学生采用分割与逼近的方法,得出利用v-t图像下的“面积”求位移的方法,进而推导出匀变速直线运动的位移公式。教材在第六节最后设置了“发展空间”栏目,其中的第二题启发学生通过v-t图像下的“面积”来表示位移，并算出变速直线运动的位移。

3 各版教材设计的对比、分析

3.1 逻辑维度

各版本教材主要涉及两种设计逻辑,分别是理论指导实践型和实践引发探究型。其中人教版、教科版和鲁科版属于理论指导实践型,教材先对匀变速直线运动的规律作理论探究,再用所得理论分析自由落体等具体问题。沪科教版和粤教版属于实践引发探究型,教材先对自由落体这个特殊的匀变速直线运动进行系统分析,再结合自由落体的研究方法及所得结论,顺理成章得到一般匀变速直线运动的规律。笔者认为,实践引发探究型教材设计更能够激发学生的问题意识,体现物理源自生活的本质,促使学生将实践和理论相结合。

3.2 方法维度

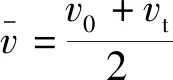
4 指向深度学习的教学建议

4.1 基于简单实例,由浅入深,层层递进

各版本教材均采用抽象公式的推导,沪科教版和粤教版虽然是从自由落体的特例入手,但依然没有涉及具体的位移、加速度和时间的数值,推导过程相对抽象。笔者建议借鉴沪科教版教材的方法,设计一个具体的匀加速直线运动,估算其位移,从而利用v-t图像下的“面积”，推导位移公式。

图1

可用以下情景导入:玩具小车从静止开始做加速度大小为a=2m/s2的匀加速直线运动,试估算小车在5s内运动位移的大小。

教师给出速度时刻表(如表1)，并引导学生画出v-t图像(如图1)。

表1

教师先启发学生提出估算方案:将每一秒内的运动当成匀速直线运动，计算相应的位移，再求和:x=2×1m+4×1m+6×1m+8×1m=20m。显然这个方案是有误差,比如2m/s只是1s时刻所对应的瞬时速度,而1～2s内速度均比2m/s大,所以实际位移也应大于以2m/s匀速运动1s所产生的位移，后面几项情况类似。此时教师可以让学生在v-t图像中画出各阶段匀速运动的v-t图像,同时将各个匀速运动对应矩形涂上阴影。此时学生已能提出更理想的估算方案了，比如每隔0.5s取一个速度进行估算,计算过程如下:x=1×0.5m+2×0.5m+3×0.5m+……+9×0.5m=22.5m。

学生在边作图、边计算的过程中,很轻松地发现:当时间取得越短,未涂上阴影的空白三角部分越来越小,估算也更精确。学生很容易得出结论:当时间取得极短时,小三角部分就消失了,这个匀加速运动的位移就可以用整个大三角形的“面积”来表示了。

通过对这个简单又具体运动的分析,学生的思维由浅入深,更容易理解v-t图像下的“面积”即位移这个结论的内涵,从而更有利于位移公式的推导。

4.2 微元法的逆向思考

所谓逆向思考是相对于正常的思考方式而言的，各版本教材均是由一个匀加速运动出发,引导学生采用“分割”方法,将匀加速运动看成是无数个匀速运动的组合。这种思维方式的难点不在于“微元思想”,而在于学生难以理解当分割的段数变多时,为什么所带来的误差会越来越小，教师可以设计一个“逆方案”来突破这个难点。

以玩具小车为研究对象,设计四组总时间均为8s的分段匀速运动,v-t图像如图2所示。

图2

运动1:第一个4s内速度为4m/s,第二个4s内速度为6m/s;

运动2:第一个2s内速度为4m/s,第二个2s内速度为5m/s,第三个2s内速度为6m/s,第四个2s内速度为7m/s;

运动3:第一个1s内速度为4m/s,第二个1s内速度为4.5m/s……第八个1s内速度为7.5m/s;

运动4:第一个0.5s内速度为4m/s,第二个0.5s内速度为4.25m/s……第十五个0.5s内速度为7.5m/s,第十六个0.5s内速度为7.75m/s。

让学生结合情景和v-t图像分别计算出这四个运动的位移分别为:x1=40m,x2=44m,x3=46m,x4=47m。

教师可以引导学生继续按照以上规律将时间细分,计算出更多的位移:x5=47.5m,x6=47.75m,x7=47.875m……

学生总结发现,如果将时间再细分,那么总位移最终指向48m。教师甚至可以引导学生根据等比数列的求和公式得出这个数列的最终求和就是48m。

教师再启发学生思考:如果将这8s等分成无数相等的时间,按此规律,显然无数个极短的匀速直线运动画出来必定是趋于一条直线,即这个复杂运动演变成了初速度为4m/s、加速度为0.5m/s2的匀加速直线运动(如图3),而这个运动的位移应该就是v-t图线和t轴所包围的“面积”，学生计算得出该“面积”为48m,与之前数学推导完全一致。通过“逆向思考”的方式,学生能够更好地掌握微元法。

图3

《普通高中物理课程标准(2017年版)》要求学生能够正确使用思维方法,从定性和定量两方面进行科学推理、找出规律。对于高中学生来讲,微元法属于高阶思维范畴,教师在教学中应由浅入深,创设具体的物理情景,启发学生步步深入,直抵物理本质。此外,合理整合各版本教材,优中取精,更有利于培养学生的高阶思维,促进学生的深度学习。