基于ABAQUS的曲梁与拱静应力分析

陈琦 唐佳 牛强强

曲梁与拱广泛应用于各种工程项目中，但约束条件对其力学性能的影响是显著的。曲率影响了对曲梁与拱结构的研究，本文通过ABAQUS 有限元软件数值模拟标准实验构件的变形情况，通过直接定义梁的法线，从而减小曲率对结果的影响，得到简支曲梁、二铰拱、无铰拱的应力最大截面和应变最大截面，为曲梁与拱在实际工程中的应用提供了参考依据。

学者Vlasov 在20 世纪50 年代建立了经典的稳定性理论，将曲梁的曲率替换，然后代入直梁的平衡方程中得到求解，开始了学者对曲梁与拱的研究。接着Usami 等在薄壁构件理论分析的基本假定，推导出曲梁翘曲位移的近似表达式，并推广至拱的研究。近年来，对曲梁的研究主要在刚度矩阵上和通过有限元进行分析曲梁的应力应变。

本文通过ABAQUS 有限元软件数值模拟了构件弹簧钢制（）的矩形断面曲杆在静应力作用下其变形结果，得到应力最大截面、应变最大截面，讨论分析了三种约束条件下曲梁与拱的静应力沿轴线变化的情况，为工程实际提供参考依据，以便于曲梁与拱结构在实际工程中的推广。

一、仿真模拟

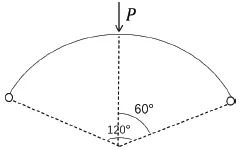
图1 研究对象示意图

所探究曲梁与拱构件的具体参数如表1 所示：

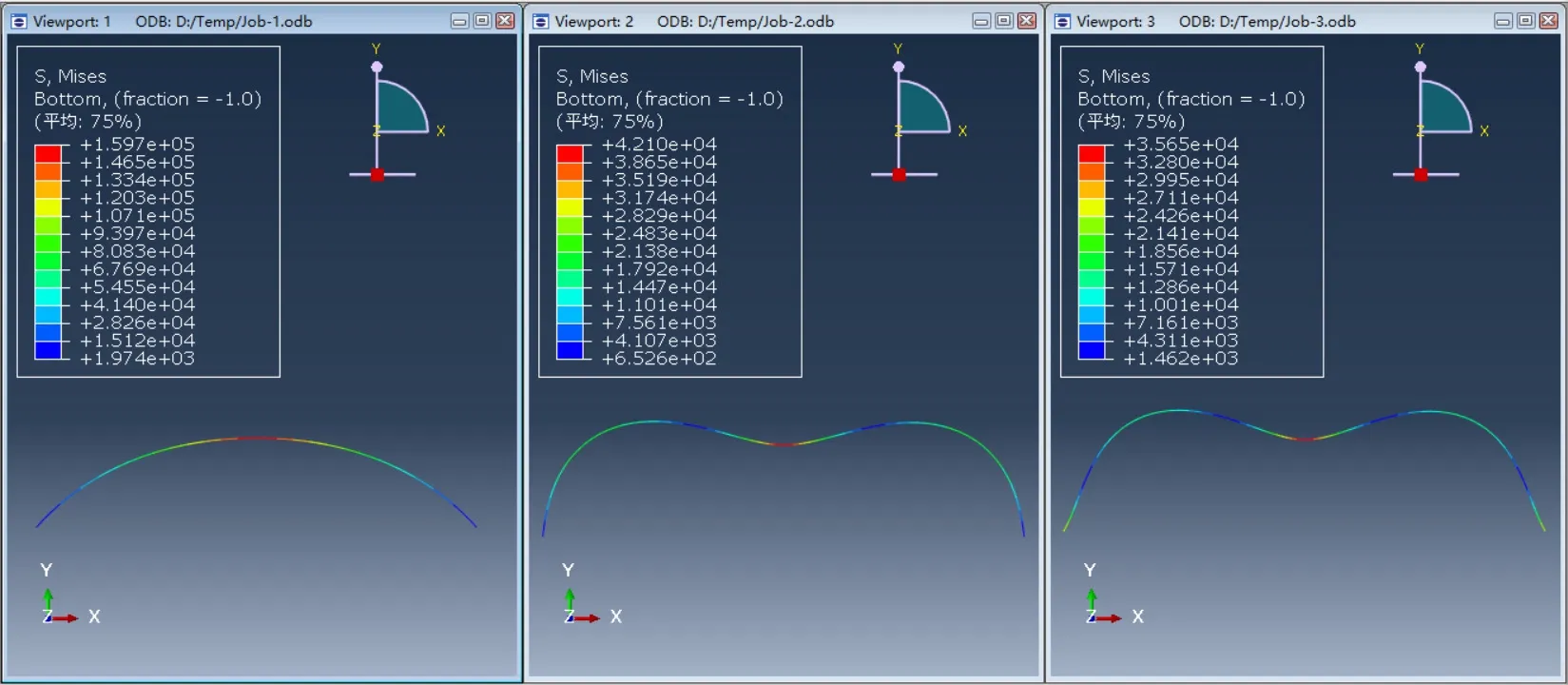
图2 三种约束条件下的应力分布云图

表1 试件相关数据

利用以上参数，在ABAQUS 中建立相应模型，得到如下应力云图结果，如图2 所示。

1.简支曲梁

数值仿真模拟得到如下简支曲梁在顶部受集中力作用下应力沿路径的变化如图3 所示。

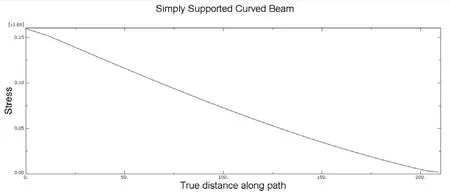
图3 简支曲梁静应力变化图像

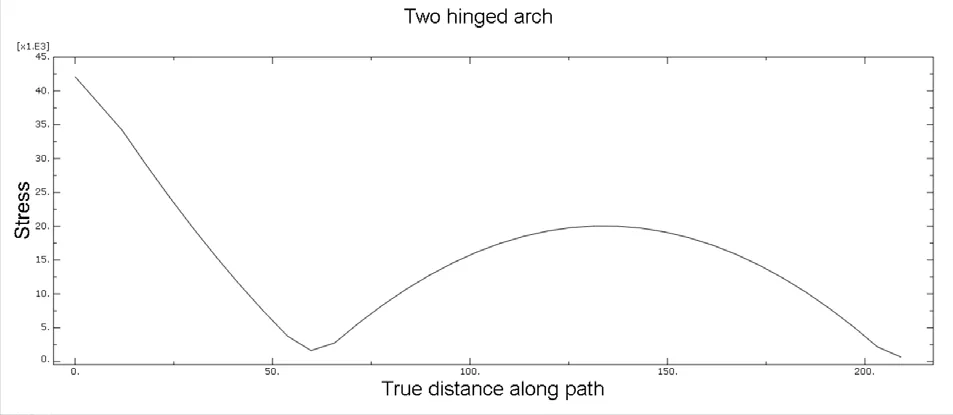
图4 二铰拱静应力变化图像

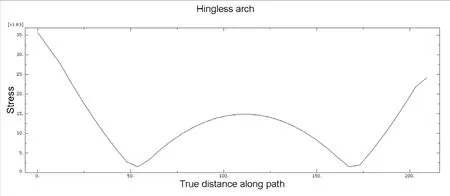
图5 无铰拱静应力变化图像

2.二铰拱

数值仿真模拟得到如下二铰拱在顶部受集中力作用下应力沿路径的变化如图4 所示。

3.无铰拱

数值仿真模拟得到如下无铰拱在顶部受集中力作用下应力沿路径的变化如图5 所示。

二、结语

对于曲梁与拱的静应力分析中，简支曲梁应力最大为 159689P× 10-5(N/mm2)时，路径为0；二铰拱应力最大为42101.5P×1 0-5(N/mm2)时，路径为0；无铰拱应力最大为35653.5P×1 0-5(N/mm2)，路径为0；从三种静应力变化图像中可以看出简支曲梁的应力变化较为平缓，避免了应力集中，出现危险点。此结论为工程实践提供了参考，保证实际工程的安全性。