粗粒土颗粒破碎效应量化分析
宋兴海, 任永旺, 刘子苑, 孙晓勇
(1. 河北水利电力学院 土木工程学院, 河北 沧州 061001; 2. 大元建业集团股份有限公司, 河北 沧州 061001)
固体材料(如钢、塑料等)在力作用下因晶体滑移错位等内因引起外观弹性及塑性变形,两者间比例不同使得材料宏观破坏形式呈延性或脆性特征[1];与固体材料不同,散粒体材料(如粗粒土、堆石料、砂集料等)在不同应力作用下因粗面磨蚀、棱角挤碎及体积破碎等颗粒行为而造成其宏观变形[2]。粒径大于2 mm砾粒及砂粒总质量分数超过50%的土料称为粗粒土,因其具有易压实、沉陷量小及强透水性等特性而被广泛应用于土木、水利、交通等领域;当应力增至一定程度时,属颗粒类材料的粗粒土极易发生颗粒破碎;此效应对土体强度、变形及渗透等力学性质与密实度等工程特性影响显著[3],成为推广此类材料工程应用的限制因素。
应力作用下颗粒破碎效应增加了土体颗粒数量及比表面积;诸多学者依据单位体积土体颗粒比表面积增量或粒径分布特征探究颗粒破碎效应机制,并提出了相关量化指标。梁越等[4]基于熵增理论认为基础熵变化规律可表征颗粒破坏特征,并将其用于量化泥岩受干湿循环作用的颗粒破碎程度;在混沌理论中熵指标用于描述均质态微观介质整体定向趋势,从测量尺度上还需深入探究将基础熵用于量化粗粒土颗粒破碎程度的合理性。考虑工程应用可操作性及便捷性,依据不同应力下颗粒破碎,查明颗粒破碎前后粒径级配曲线(Particle Size Distribution Curve,PSDC)并建立相应量化指标是揭示粗粒土颗粒破碎程度的直接有效途径。基于此,当前存在三种主要方法:一是取破碎前后PSDC间差的绝对值代数和作为量化指标,如颗粒破碎量Bg[5];二是基于破碎能量理论量化PSDC与坐标轴所围面积而建立的破碎指标,如颗粒相对破碎率Br[6];三是基于破碎前后颗粒分布特征局部与整理存在相似性的分形理论而建立的分形指标,如分形维数D[7]。
在同一应力条件下土体颗粒破碎规律相同,三个指标虽从不同角度量化破碎程度,其度量效果应相近,即各指标间应存在内在联系,但鲜有文献对此描述。为此,根据不同应力条件下粗粒土受剪切作用破坏前后颗粒粒径分布,查明PSDC变化形态,探讨破碎程度量化指标Bg,Br,D间联系,揭示粗粒土颗粒破碎效应量化指标换算关系,为工程中计算粗粒土考虑颗粒破碎所致沉降变形提供参考。
1 粗粒土三轴试验
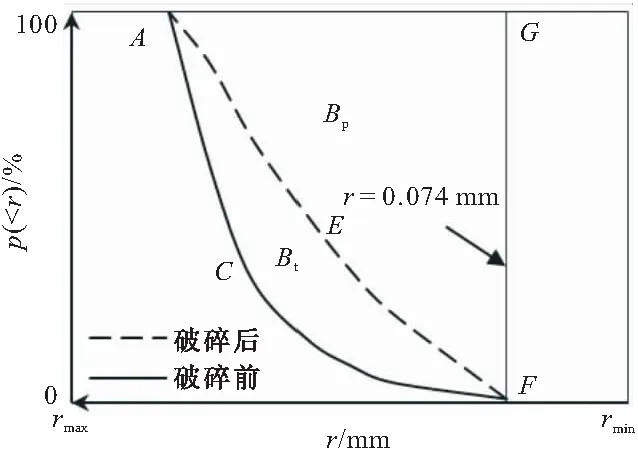
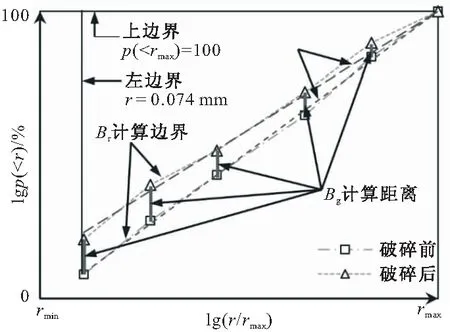
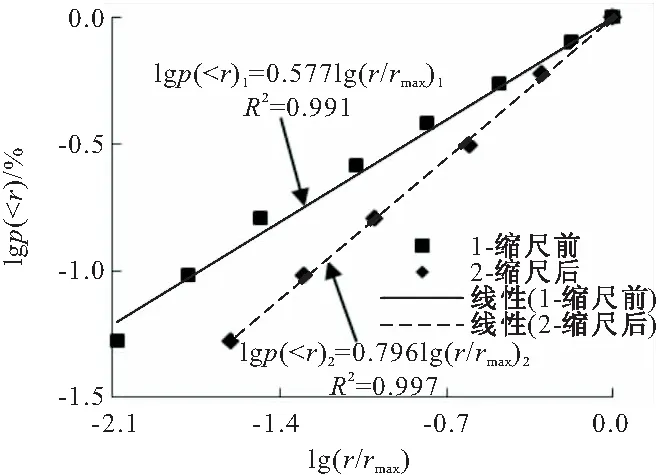
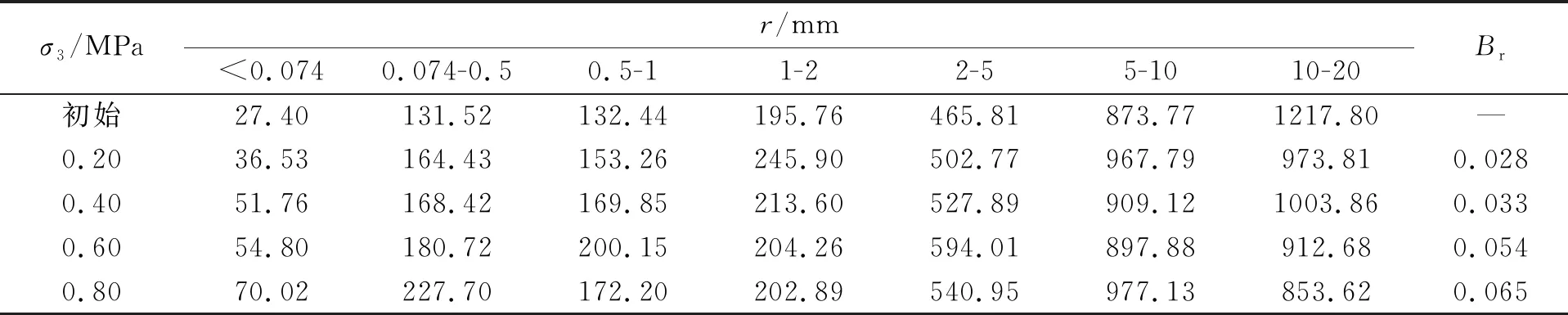
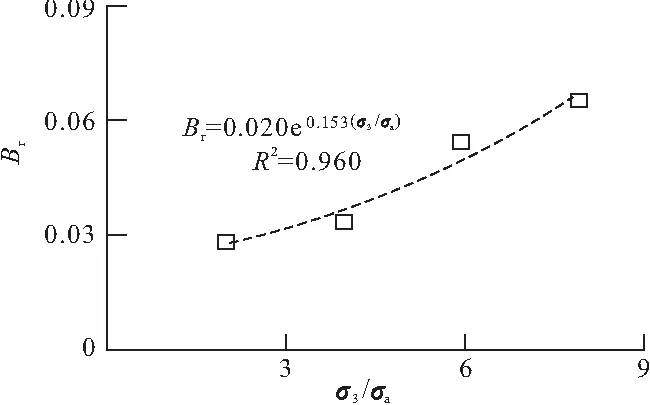
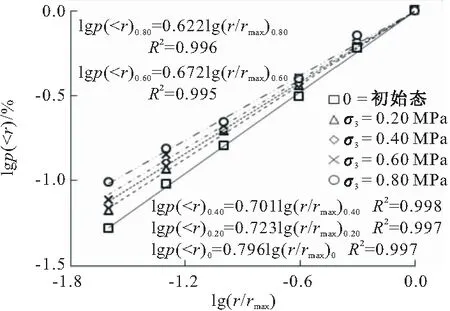
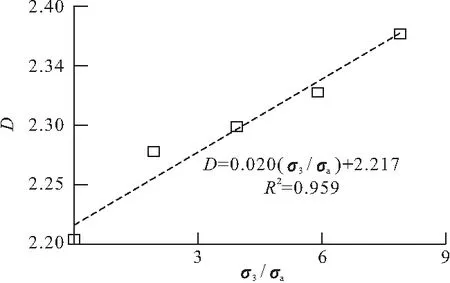
试样土体取自河北沧州某港口填筑区所用填料(其母岩为青白口系井儿峪组砂岩,微风化,隐晶砂质结构,主要矿物成分为石英及长石),粗粒(颗粒直径大于2 mm)含量为78%,颗粒比重为2.67,自然含水率为8.56%,原级配最大粒径为60 mm。受试验仪器尺寸限制,依据规范[8]采用混合法对原级配作缩尺处理,缩尺后最大粒径为20 mm,缩尺前后土体不均匀系数Cu为22.86及8.86、曲率系数Cc为1.68及2.36,均为级配良好粗粒土,其PSDC见图1(r为颗粒直径,p( 图1 缩尺前后粗粒土PSDC 采用GDS三轴试验仪作不同围压下土体三轴固结排水试验(Consolidation Drainage Test,CD试验),固结阶段采用应力控制施加静水压力,剪切阶段采用应变控制对土体施加剪切应力直至破坏,传感器自动采集试验过程数据。试样尺寸为直径101 mm、高200 mm,制样干密度为1.90 g/cm3(即压实度为90%时土体干密度值),初始含水率为10%。设定围压σ3值为0.20,0.40,0.60,0.80 MPa。 三轴剪切试验主要有两个阶段:(1)围压阶段,施加围压σ3至设定值,并保持30 min;(2)剪切阶段,施加偏应力Δσ至试样破坏,以轴向剪切应变达15%作为试验结束控制标准。试验结束后将试样置于105 ℃恒温条件下烘干24 h,采用20~10,10~5,5~2,2~1,1~0.5,0.25~0.5,0.074~0.25 mm及<0.074 mm圆孔筛网作振动过网的筛分处理;随后采用精度为0.01 g电子称测定各筛网剩余颗粒质量,用于进一步分析。 2.1.1 指标破碎量Bg Marsal[5]分析了粗粒土PSDC分布,指出单一特征粒径不能反映颗粒破碎效应整体特征,建议采用多粒径指标Bg表征颗粒破碎程度。 对于同一级配粗粒土,同一尺寸下土体颗粒破碎前后PSDC存在差值ΔWi,如图2所示;将所有差值作代数累加即可得到Bg值,其计算公式见式(1)(2)。 ΔWi=Wia-Wib (1) (2) 式中:Wia为试验前PSDC上某粒径值;Wib为试验后PSDC上某粒径值;n为选择粒径的数目。 图2 破碎指标Bg 2.1.2 指标相对破碎率Br Hardin[6]将0.074 mm作为粗粒土颗粒破碎终止粒径,粒径大于0.074 mm的颗粒存在破碎势函数bp,其数学表达为: bp=lg(r/0.074) (3) 从式(3)可知,bp为r单值函数,表征单个颗粒破碎可能性;土体破碎势bp在p( (4) 式中:f为PSDC数学函数。 图3 量化指标Br 若在不同应力下,土体发生颗粒破碎,则破碎后土体PSDC将演化为曲线AEF;此时,土体破碎量为Bt,其数值为: (5) 式中:Bpb为颗粒破碎前土体破碎势;Bpa为破碎后土体破碎势。 考虑PSDC形态变化,用Bt与Bp间比值Br来表征不同颗粒组成土体的颗粒破碎程度。 Br=Bt/Bp (6) 2.1.3 分形指标D 分形理论盒维数法及其发展被引入土力学并用于描述粗集类材料颗粒分形特性演变规律,并建立了粒径-质量分形模型[7]。假定某体积V中粗粒土颗粒总数为N0,质量为M0,粒径不小于r的颗粒数目为N(≥r),质量为M(≥r)。由盒维数法可得粒径小于r的颗粒N( N( (7) 式中:C为系数;D′为分形维数,0≤D′<3。 式(7)两边同时对r求导,得到dN( dN( (8) 若土颗粒密度为ρ,用系数C1表示概化颗粒形状,球形时取π/6,块体时取1。对式(8)作积分运算,则: (9) 将式(8)带入式(9)可得到: (10) 由式(10)可得到M0的数学表达为: (11) 在PSDC中p( p( (12) 将式(10)及(11)代入式(12),整理得到: (13) 从式(13)可知,用D′,rmax,rmin量化表述粗粒土PSDC;因D′为0~3,且rmin相对较小,rmin/rmax≈0,则忽略rmin/rmax,D′≈D,则式(13)简化为: p( (14) 式(14)两边同时取对数,得到: lgp( (15) 由式(15)可知p( 2.1.4 指标度量分析 根据前述分析可知,量化指标Bg,Br,D均为在p( 图4 同一坐标下量化指标 在图4中,Bg为颗粒破碎前后数据点间距离(一维)代数和;Br及D均为二维平面内概化颗粒破碎效应,其上边界(p( 保持缩尺前后土体力学性质相似,并将试验所得规律等比尺应用于工程建设是进行室内试验并改进其方法的基础[9]。从组成土体颗粒尺寸角度可知,一定程度上室内试验缩尺方法是一种既定的颗粒“破碎”行为[10],即超粒径全部缩至为试样允许粒径范围。这种缩尺效应直接影响室内试验成果对原型的模拟准确程度。 根据式(3)~(6)整理图1中数据,采用CAD 描绘形式计算得到缩尺前后后土体Br为0.125。用式(15)整理缩尺前后PSDC,得到土体PFC,并用线性函数拟合其变化趋势,如图5所示。从图5可知,拟合参数R2均超过0.95,线性相关性显著;缩尺前D1为2.423,缩尺后D2为2.204,后者比前者减小约9.04%。由此可知,采用混合法对原级配进行缩尺处理[11],减小了大颗粒数量、增加了稍小颗粒含量;这种缩尺效应可用颗粒破碎指标Br或D进行量化,应将此效应作为试验方法误差进行土体室内力学性质及工程性质分析。 图5 缩尺前后土体PFC 粗粒土颗粒受压剪作用而达到极限强度时产生颗粒破碎,其破碎程度受应力状态影响。 2.3.1Br量化分析 整理筛分结果,统计不同围压下土体各粒组颗粒质量,采用2.1.2节中计算方法,得到不同应力下土体颗粒破碎程度量化指标Br值,见表1。从表1可知,土体中大颗粒在应力作用下破碎、分裂为小颗粒,且其破碎程度与围压密切相关。 表1 试验前后土体颗粒筛分结果(质量) g 在同一坐标下绘制Br与相对围压σ3/σa(σa为大气压强,取0.101 MPa)分布,见图6。从图6可知,Br随σ3/σa增大呈指数函数变化趋势,拟合数学方程为式(16),且拟合参数R2为0.960,指数关系显著。 Br=0.020e0.153(σ3/σa) (16) 图6 Br随σ3/σa分布 2.3.2D量化分析 根据式(15),整理表1试验数据,得到不同σ3时lgp( 图7 lgp( 由图7可知,PFC的斜率随σ3增大而逐渐减小,D逐渐增大;与之相应,细粒逐渐增多,粗粒减小。与Br相似,整理图7中计算所得D,在同一平面内绘制D-σ3/σa分布,见图8。在图8中,D随σ3/σa的线性变化趋势显著,其拟合方程为式(17);因D<3,则σ3<3.95 MPa,即式(17)适用于粗粒土小主应力处于0~3.95 MPa间剪切破坏时D计算。 D=0.020σ3/σa+2.217,0<σ3<3.95 (17) 图8 D随σ3/σa分布 2.3.3Br-D方程建立 联立式(16)(17),消去σ3/σa得到Br与D的函数方程,见式(18)。 D=0.131ln(Br)+2.728,0.02 (18) 从式(18)可知,当Br趋于下限0.02时,D渐近其下限2.217;当Br趋于上限1时,D渐近于上限2.728。这表明,粗粒土分形维数存在边界值,这与粗粒土原有级配曲线所呈分形特征相关;总体上,在经受不同应力下剪切作用能量耗散(即存在颗粒破碎效应),粗粒土分形维数随相对破碎率增加呈对数关系变化。 不同应力作用下散粒体材料颗粒破碎主要有三种形式:粗面磨蚀、棱角挤碎及颗粒破碎[2]。在外荷载作用下,颗粒存在滑移、翻转及棱角挤碎等位置调整,机械咬合及粗面摩擦等粒间接触形式与空间上镶嵌搭接等团粒堆叠结构共同形成粗粒土受力骨架[12,13];应力持续增加至一定程度时,受力骨架中局部颗粒所受应力超过其强度而发生破碎现象[14]。不同围压条件下土体颗粒破碎程度存在差异,围压越高,土体受剪应力直至破坏过程颗粒间接触切向与法向应力愈大,颗粒破碎程度愈高,如图6,8所示。 从量化颗粒破碎准确程度角度,二维指标(Br,D)高于一维指标Bg,且Br优于D,如图4所示。实际工程中,颗粒类材料使用时粗粒土应力状态分布广泛,颗粒破碎前后PSDC差异不显著,此时采用Br量化其破碎效应时将受测定计算者人为确定Bp面积影响,存在偶然误差,此时可考虑采用D进行量化颗粒破碎,并采用式(18)对其进行校核。 依据PFC线性分布特征计算D,是分形理论的一种特殊情况,在局部与整体存在相似性的自然规律下[15],还需深入分析与提炼其与现有度量指标间的联系与区别,更深入挖掘分形理论的适用性。 (1)在粒径累积百分比-粒径平面内论述颗粒破碎量化指标Bg,Br,D的建立基础及其相互间区别。Bg为数据点间距离代数和,属一维指标。Br,D均基于面积变化量刻画颗粒破碎程度,属二维指标;Br为数据点折线距离总和比较,D为数据点所概化直线斜率变化量,本质都是利用增量量化破碎程度。 (2)处理超粒径的缩尺方法是一种既定的颗粒“破碎”行为,可用Br或D量化。用破碎势量化混合法缩尺效应Br为0.125,用分形理论得到土体缩尺后分形维数减小9.04%,建议室内试验应将缩尺效应作为试验方法误差。 (3)粗粒土不同应力下受剪切作用,其分形维数随相对破碎率增加呈指数关系变化。Br随相对围压σ3/σa增大呈指数变化趋势,D随σ3/σa变化呈线性分布规律,进而得到D与Br为对数函数关系。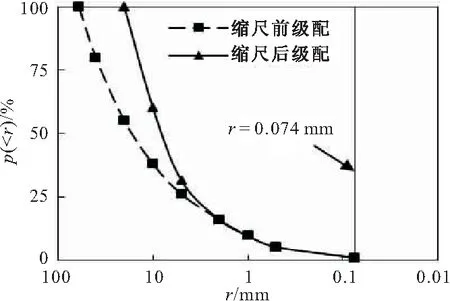
2 颗粒破碎效应分析
2.1 颗粒破碎量化指标

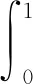
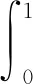
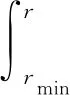
2.2 缩尺效应颗粒破碎分析
2.3 不同应力时颗粒破碎分析
3 颗粒破碎讨论
3.1 颗粒破碎机制
3.2 量化指标适用性
4 结 论

