干湿循环作用下砂岩蠕变损伤及本构模型

霍树义， 金坎辉， 杨 涛， 周晴晴， 张 薇， 崔建军

(1. 河北水利电力学院 后勤管理处， 河北 沧州 061001； 2. 河北省南运河河务管理处， 河北 沧州 061001)

近些年来，我国社会经济取得了飞跃发展，在矿业工程、水利工程、交通工程等领域齐头并进且大有赶超欧美国家的趋势，在这些工程建设中，或多或少会赋存于一定的水环境，受水岩相互作用的影响，岩体的强度、变形以及其它力学特性均会产生明显变化，进而引发一系列工程问题。其中，干湿循环作用对岩石的损伤劣化以及工程地质稳定影响显著，开展干湿循环作用下岩石的力学行为研究具有理论和工程实践意义[1～3]。

砂岩是一种多孔介质岩石，由固体骨架、孔隙及其它矿物质组成，是现代工程建设领域中最为常见的岩石种类之一，在干湿循环作用下关系着边坡稳定等一系列工程问题[4,5]。张鹏等[6,7]对干湿循环作用下砂岩的强度劣化规律进行了分析，得到了强度和弹性模量等与干湿循环次数的关系；薛晶晶等[8]对长英质细砂岩和弱蚀变泥质砂岩两种砂岩在干湿循环下的强度特征进行了对比研究，发现长英质细砂岩经干湿作用后的强度下降幅度大于弱蚀变泥质砂岩；当前，对砂岩干湿循环作用下强度及变形行为的研究较多，且逐渐由宏观破坏向微观损伤方向发展[9～11]；宋朝阳等[12]将砂岩在干湿循环作用下的微观损伤特征与声发射技术相结合，利用声学技术研究其力学性质的变化。

目前，针对砂岩干湿循环作用下的力学行为主要集中于常规加载和变形方面，对于干湿循环砂岩的蠕变力学行为的研究还比较鲜见[13]，由于工程建筑要求保持长期的安全与稳定，因此单纯的短期力学特征已不能满足工程设计和施工需要。基于此本文开展了干湿循环作用下砂岩的宏细观蠕变损伤变形的研究，基于研究结果建立起考虑干湿循环次数的分数阶蠕变模型，以期能够较好描述不同干湿循环作用下砂岩的蠕变损伤全过程。

1 试验概况

试验岩芯取自山西某矿山地下深约300 m处，中等粒径砂岩，平均密度2.31 g/cm3，孔隙率为7.8%，经D/Max-3B 型 X射线衍射仪测试得到：石英、长石、方解石、泥质胶结物等为砂岩主要成分。选取几组理化性质最为接近的岩芯，对岩芯按照相关试验规程和标准，进行切钻、切、磨加工，制成Φ50 mm×H100 mm的标准圆柱形试件。将试件分为五组，一组为原始试验对照组，即不进行干湿循环，其余四组分别进行“饱水-烘干”循环作用，循环次数分别为5，10，15，20次，干湿循环方式为：在常温下将试件置于自来水中浸泡(每隔2 h进行一次称重，前后两次称重差值小于0.1%时停止)，然后将试件在105 ℃烘箱中进行除湿干燥(每隔2 h进行一次称重，前后两次称重差值小于0.1%时停止)，即完成一次“饱水-烘干”循环。

首先对各试验组进行单轴抗压试验，得到各试验组的抗压强度、弹模等参数与干湿循环次数的关系；其次，再对各试验进行单级蠕变加载试验，恒定加载应力为单轴强度的40%，60%，80%，90%，95%，蠕变试验具体步骤为：(1)将饱水-烘干后的试件用保鲜膜包裹，防止蠕变试验过程中试件内部水分发生变化，然后置于试验台上并进行预加载，将试件固定，安装应变仪；(2)将试件施加至预定应力值，保持恒定应力，进行蠕变试验；(3)在恒定应力下，若120 h内发生蠕变破坏，则试验停止，若没有发生蠕变破坏，试验进行至120 h后也停止试验，测试砂岩的蠕变应变及损伤情况。试验仪器及试件见图1。

图1 实验仪器及试件

2 单轴压缩试验结果分析

试验得到的不同干湿循环次数下砂岩的应力-应变曲线特征见图2。从图中可以看到，在不进行干湿循环的情况下，砂岩的应力-应变呈脆性破坏特征，即压密和屈服阶段不明显，弹性阶段持续时间较长，峰后曲线较陡；在低干湿循环次数(5，10次)下，砂岩的应力-应变曲线与对照组相比呈现一定的变化，具体表现在屈服阶段区域增长，峰后破坏的脆性减弱，即逐渐变为脆-延性破坏；当干湿循环次数增至15，20次后，砂岩的脆性已较弱，压密和塑性屈服变形十分明显，弹性阶段时间较短，峰后曲线变化平缓，表现为典型的延性破坏特征。在干湿循环作用下，砂岩内部发生理化性质的改变，孔隙结构发生变化，颗粒间胶结力逐渐降低，屈服变形在试件内部是逐步发生的，峰后破坏阶段主要靠碎块间摩擦阻力和机械咬合力支撑变形，在低循环作用下颗粒剥落数量较少，因而表现为脆性破坏，当干湿循环次数增多后，颗粒剥落较多，填充于砂岩破裂面之间，起到一种缓冲变形的作用，故而表现为延性破坏特征。

图2 不同循环次数下应力-应变曲线

表1为试验得到的不同循环次数下砂岩的强度和弹性模量的测试结果。从表中可以看出：随着干湿交替次数的逐渐增加，砂岩的强度呈对数型函数σ=78.12-2.29ln(1+n6.16) 降低，干湿循环作用后，砂岩的结构变得松散，颗粒之间的胶结连结力降低，导致砂岩的强度减小；弹性模量与循环次数之间呈指数型函数E=11.08n-0.052降低；在干湿循环作用前期，强度和弹性模量降低幅度较大，随循环次数增加，对砂岩的理化损伤效应逐渐减弱，强度和弹模的降低幅度逐渐减小并趋于平缓。

表1 力学强度测试结果

3 蠕变试验结果分析

3.1 蠕变曲线特征

图3为试验得到蠕变应变历时曲线。从图中可以看出：在相同干湿循环次数下，随着加载应力的增大，瞬态应变越大，砂岩的蠕变历时曲线呈不同的变化特征，低应力水平时，蠕变状态仅包括初始蠕变和稳态蠕变阶段，特别是在低干湿循环次数下，蠕变速率呈收敛趋势，在试验时间内没有加速蠕变阶段出现，在高应力下包括典型的蠕变三阶段：“初始-稳态-加速”，应力越高，蠕变破坏的时间越短，这是因为应力越大，蠕变损伤发展越快，累计损伤效应越明显；在同等应力水平下，干湿循环次数越多，瞬态蠕变越大，稳态蠕变率越高，但蠕变破坏的时间越短，这主要是因为在干湿循环作用下，颗粒间胶结力明显降低，砂岩内部的初始损伤越明显，故而使得砂岩损伤发展越快；在规定试验时间内，对照试验组的砂岩在90%和95%加载应力下才发生蠕变破坏，在其它应力水平下没有发生，在5，10次干湿循环作用下，发生蠕变破坏对应的应力为80%，在15，20次下，发生蠕变破坏对应的应力水平为60%；在同等应力水平下，循环次数越多，蠕变破坏的时间越短；相同干湿循环次数下，应力水平越高，破坏时间越短。

图3 不同应力水平下的蠕变历时曲线

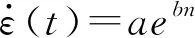
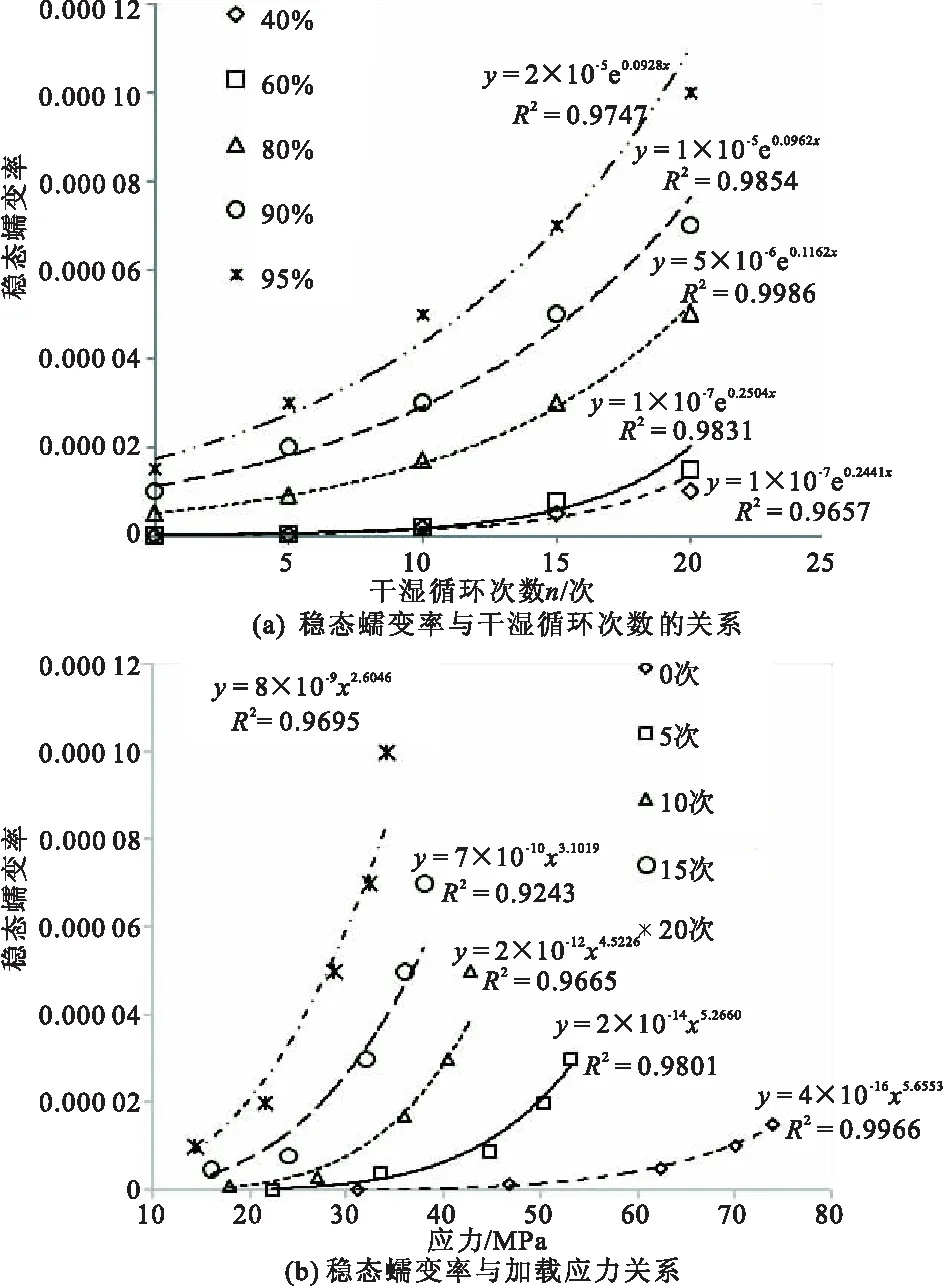
图4 稳态蠕变率变化特征

图5 敏感性常数与干湿循环次数关系

3.2 长期强度特征

长期强度关系着工程的长期稳定性问题，长期强度的求取一般有等时应力应变曲线法、体变法、蠕变速率拐点法等。鉴于等时应力-应变曲线法求取复杂，而稳态蠕变速率拐点法适应性差等特点，因此本文选择文献[14]提出的改进稳态蠕变速率拐点法对长期强度进行研究，该法的主要求取手段为通过对稳态蠕变速率进行求倒数，以应力为横向坐标，稳态蠕变速率倒数为纵向坐标，分别找出低应力稳态蠕变速率倒数和高应力稳态蠕变速率倒数的线性关系，将两条线性拟合曲线延长并相交，相交点对应的应力即为长期强度，见图6。通过改进的稳态蠕变率拐点法得到的长期强度与短期强度的关系见表2，从表2中可以看到，随着干湿循环次数的增加，砂岩的长期强度值逐渐降低，其与短期强度的比值也呈逐渐减小趋势，不进行干湿循环时，长期强度与短期强度的比值为0.603，当干湿循环20次以后，长期强度σs与短期强度σ的比值仅为0.416，可见干湿循环在很大程度上加剧了砂岩内部的损伤，致使长期承载力显著降低。

图6 改进的稳态蠕变速率拐点法示意

表2 长期强度与短期强度值关系

3.3 蠕变损伤演化特征

Kachanov[15]通过研究认为单轴压缩情况下，岩石的蠕变与损伤因子间呈如下关系：

(1)

式中：D为损伤因子；tF为岩石蠕变寿命；V为与材料相关的计算参数；t为蠕变历时。

假设岩石在天然状态下的损伤为0，经干湿循环后的损伤值可以用弹性模量来表示：

(2)

式中：D0为经n次干湿循环后的初始损伤；En为经n次干湿循环后的弹模；E0为天然状态下的弹模。考虑岩石的初始损伤，因此，可将式(1)(2)联立，得到：

(3)

定义En/E0=λ为损伤因子修正系数，经表1试验分析数据计算可得干湿循环0，5，10，15，20次后的修正系数λ为1，0.738，0.549，0.443，0.352。

蠕变破坏时间可以利用下式进行计算：

(4)

联立式(3)(4)，最终得到蠕变损伤因子与时间t的关系：

(5)

首先将蠕变试验数据分别代入式(4)，得到不同循环次数下砂岩的A和V值，见表3，将A，V，λ以及应力值代入式(5)，可以得到任意应力水平下的蠕变损伤发展过程，见图7。结合表3和图7可以看到：砂岩的初始损伤随干湿循环次数的增加逐渐增大，表明干湿循环对砂岩的劣化度越高，因此蠕变过程中损伤累积较快，蠕变破坏时间段，在天然状态下，砂岩的蠕变损伤值仅为0.164，可以预见，在此应力环境中，砂岩还需要很长一段时间才发生蠕变损伤破坏；相同干湿循环次数下，随着应力水平的提高，损伤发展呈现不同变化特征，低应力水平下，损伤发展缓慢，基本与x轴平行，在中等应力水平下，内部损伤在发展，但呈线性增长关系，且斜率较小，高应力水平下，损伤发展呈指数型函数关系，当试验进行到一定时间后，损伤快速累积，表明此时砂岩内部结构发生实质性变化，已不能继续支撑其结构的完整性，预示着即将发生蠕变破坏；同等时间里，应力水平越高，损伤值越大。

表3 计算参数值

图7 蠕变损伤因子演化规律

3.4 蠕变本构模型研究

岩石的蠕变特性关系着工程的长期安全与稳定，近些年来，很多专家学者致力于岩石的流变本构模型的研究。为充分表达岩石加速蠕变阶段的蠕变变形过程，分数阶模型被广泛应用于描述岩石的蠕变全过程[16]。结合蠕变试验结果，定义砂岩的蠕变本构方程为(见图8)：

(6)

式中：η1，η2为黏弹性系数；β，γ为分数阶微积分阶数；ta，εa分别为加速起始时刻及对应的应变量。

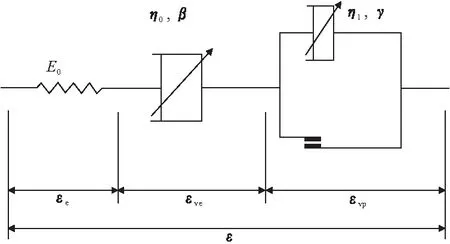
图8 分数阶黏弹塑本构模型

本构模型中，将粘滞性系数看作一个定常数是不准确的，大量研究表明：当岩石在低于长期强度下，只发生蠕变硬化作用，当应力大于长期强度后，会发生硬化与损伤双重作用，并且损伤作用会逐渐超过硬化作用，岩石会发生蠕变加速破坏，根据前人研究成果[17,18]，认为岩石的粘滞性系数符合如下关系：

(7)

式中：η10为初始粘滞性系数；ta为加速蠕变开始时刻；B，ζ，c，m为非线性常数。

通过前文分析可以得到：砂岩的瞬时弹性模量与干湿循环次数呈指数型函数关系，而应力敏感性常数d又与n呈线性相关，即：

E=11.08n-0.052

(8)

d=-0.165n+5.883

(9)

由此，联立式(6)～(9)，可得考虑干湿循环影响的砂岩分数阶蠕变损伤本构模型：

(10)

上式不仅考虑了砂岩经干湿循环后的初始损伤，同时考虑了蠕变过程中的损伤时变效应，因此，能比较真实地反映砂岩的蠕变损伤全过程。对式(10)进行参数敏感性分析，见图9。从图中可以看出：随着干湿循环次数的增加，砂岩的稳态

图9 敏感性分析

蠕变率和蠕变变形量均逐渐增大，非线性加速蠕变特征越明显，可较好地反映砂岩在不同干湿循环次数下的蠕变损伤全过程。

利用文中建立的本构模型，对不同循环次数下的砂岩试验数据进行拟合，限于篇幅，本文选取每组砂岩80%加载应力下的蠕变试验数据进行非线性拟合，拟合结果见图10。从图中可以看出，不同干湿循环次数下的本构模型拟合数据与试验数据均有较高的吻合度，其相关系数R2均大于0.95，且能够很好描述初始、稳态和加速三个阶段的蠕变变化过程，特别是加速蠕变阶段的非线性特性拟合吻合度较高，表明了本文所建非线性蠕变损伤分数阶本构模型具有很好的拟合精度，能较为准确地预测砂岩在经历不同干湿循环作用后的蠕变损伤及变形发展趋势。

图10 本构模型拟合数据与试验数据对比

4 结 论

(1)砂岩经干湿循环作用后，强度随干湿循环次数增加呈对数型函数降低，弹性模量随干湿循环次数增加呈指数型函数降低。

(2)干湿循环作用会加剧砂岩内部结构的劣化，由于理化性质发生改变，软化及塑性变形能力提高，导致蠕变应变发展越快，非线性加速蠕变特征越明显；在规定试验时间内，低应力状态下，仅出现初始和稳态蠕变，在高应力状态下才会出现加速蠕变破坏；循环次数越高，发生蠕变破坏应力水平越低；稳态蠕变速率分别与干湿循环次数、应力水平呈指数型、幂函数型关系。

(3)在天然状态下，砂岩的长期强度为短期强度的60%以上，但经干湿循环作用后，长期强度与短期强度的比值显著降低，20次干湿循环后，仅为40%；干湿循环导致蠕变损伤发展出现明显差异，循环次数越多，应力水平越高，初始损伤值越高，损伤累积速率越快。

(4)基于试验分析成果，建立起考虑干湿循环损伤作用的非线性分数阶蠕变本构模型，经拟合分析，该模型可以很好地表达不同干湿循环作用后砂岩的蠕变三阶段变化特征，具有一般普适性。