基于随机森林的混凝土早期碳化预测

吴贤国， 王 雷， 邓婷婷， 胡 毅， 袁福银， 李铁军

(1. 华中科技大学 土木工程与力学学院， 湖北 武汉 430074； 2. 中交第二航务工程局有限公司， 湖北 武汉 430040； 3. 中交路桥建设有限公司， 北京 100027； 4. 中国交通建设股份有限公司， 北京 100088)

混凝土的碳化是混凝土所受到的一种化学腐蚀。水泥性质、混凝土强度、及混凝土组成成分与混凝土的碳化都有密切关系。近年来，提高混凝土结构耐久性一直是一个备受关注的问题，而混凝土早期碳化作为影响混凝土耐久性的因素之一，屡次成为研究人员争论的焦点，混凝土快速碳化的原因、混凝土早期碳化的严重后果、如何减轻混凝土碳化等问题正困扰着诸多研究学者们。

因此，国内外学者围绕混凝土碳化分析开展了相关研究。部分学者从微观方面揭示出混凝土早期碳化的实质，对混凝土早期碳化现象有了初步认识，胡晓鹏等[1]对掺合料混凝土早期碳化进行微观分析，利用测试pH值探究碳化深度规律并验证了酚酞试剂测试的适用性；胡晓鹏等[2]通过混凝土早期碳化性能的试验研究，发现了混凝土早期碳化的特点。一些学者通过在暴露条件下建立混凝土早期碳化试验，建立了不同的影响系数的表达式，胡晓鹏等[3]通过粉煤灰混凝土早期碳化规律研究，建立了粉煤灰混凝土早期碳化深度的计算模型；张成中等[4]通过探究掺合料对混凝土早期碳化深度的影响，建立了掺合料碳化速度影响系数的表达式；朱红英等[5]通过挖掘粉煤灰不同掺量对混凝土碳化的影响，混凝土的碳化深度D与碳化龄期T之间的关系可用幂函数D=αTβ(α为碳化性能影响系数；β为碳化速率影响系数)进行相关性较好的表达。还有部分学者会根据特定的实验模型，探究不同影响因素对碳化深度的影响，汪彦斌和蔺鹏臻[6]制作了一组混凝土箱梁模型在不同工况下进行一系列碳化试验,分析了箱梁结构的碳化深度在碳化时间和浓度的变化下所造成的影响，同时在理论层次上为接下来荷载作用下的箱梁碳化研究奠定了基础。然而，以上研究都是基于已有的实验数据对早期碳化特点进行挖掘，缺乏对早期碳化性质进行预测。

本文将以松原至通榆段高速公路项目为例，针对研究区季节性冻土特点，基于随机森林算法回归预测模型，选取水泥强度、水胶比、粉煤灰用量、细集料用量、粗集料用量、平均粒径等九个影响因素，从而建立早期碳化深度的随机森林预测模型，同时与BP(Back Propagation)人工神经网络预测模型及小波神经网络分析模型结果进行对比，验证随机森林模型的可靠性和适用性，为混凝土早期碳化预测提供一种新思路。

1 方法及原理

1.1 随机森林回归算法

在2001年Breiman[7]提出来随机森林(Random Forests，RF)的概念。这种算法是由Bagging(套袋)算法以及CART(Classification And Regression Tree)算法相融合而成的一种新型算法。若干个样本是利用自助抽样法(Bootstrap)从最初原始样本集中随机抽取的，并对这些样本分别构建决策树，继而形成组合分类器，假设这个随机森林的组合分类器为{h1(x),h2(x),...,hk(x)}，h(x)为单个分类器对于输入向量X所产生的输出结果。对于通过自助法(Bootstrap)随机抽取的训练集向量X，Y，Y是训练集中的对应分类结果，定义间隔函数(Margin Function)如下：

(1)

式中：k为分类器训练次数；I()为指示函数，其作用是衡量平均正确分类数大于平均错误分类数的程度；∂vk为取间隔函数值的平均值。间隔函数越小，模型分类的置信水平越低[8]。泛化误差是用来反映模型好坏程度的指标，可以表现除训练集以外的数据对模型的预测水平，随机森林泛化误差PE*为：

PE*=EX,Y(mg(X,Y)<0)

(2)

式中：EX,Y为X，Y空间上求得的概率。

随机森林预测模型的特征如下：

(1)当k趋向于无穷大时，即此时随机森林处于很大的规模，便满足大树定律规律，则随机森林泛化误差PE*如式(3)所示：

PE*=EX,Y(Pθ(h(X,θ)=Y))-

(3)

式中：θ为单棵决策树服从独立同分布的随机变量；Pθ为随机变量输出值的发生概率；X为自变量。这表明了即使随机森林的泛化误差非常大，这个模型也不会产生过拟合的情况，因为泛化误差一定存在一个极限值。

(2)假设对所有的θ，E(Y)=EXh(X,θ)则有：

(4)

1.2 随机森林的生成方法

采用Bagging 思想，从原始样本中在抽取的若干个训练样本的过程中采用了Bagging思想，且整个过程是满足随机性并是有放回抽取的，以避免随机森林决策树中出现局部最优解问题[9]。同时每个训练样本数等于原始样本数，其中回归决策子树T由每个训练样本分别建立，最后预测结果由各棵树的综合平均值表示。在Booststrap抽样时，未被抽取数据的概率为：

(5)

当N→∞时，

(6)

即表明每次有36.8%的数据未被抽取，这些数据称为袋外数据(Out-of-Bag，OOB) ，OOB误差通过OOB估计(Out-of-Bag Estimation)获得[10]。从原有的特征中选取m个特征进行最优分割点筛选，重复上述步骤生成决策树，最终的回归结果由各个决策树的输出结果求平均得到。Bagging 思想可以在保证随机性的条件下建立大量回归决策子树的同时，保证了各个子树之间的相对独立性[11]。

1.3 基于随机森林的重要性排序

OOB残差均方是一种评估随机森林特征重要性的方法，这种方法的评估依据是随机置换残差均方减少量。采用OOB残差均方进行重要性评估的大致步骤如下：

(1)每一棵回归决策树由对应的样本集建立，在预测的时候采用OOB测试集，就可以得到OOB残差均方。

(2)在b个OOB 样本的基础上，通过随机置换的方式，变量Xi形成一个新的OOB集合，这个新的OOB由已经形成的随机森林进行模拟测试，便可得到OOB的残差均方MSEij，生成矩阵A如下：

(7)

式中：p为影响因素变量个数；b为样本个数。

(3)变量Xi的scorei(重要性得分)可表示为：

scorei= ∑( errOOB2-errOOB1)/ntree

(8)

式中：errOOB1为随机森林中每一棵决策树的袋外数据误差；errOOB2为随机地对袋外数据OOB所有样本的特征Xi加入噪声干扰后每一棵决策树的袋外数据误差；ntree为决策树数目。

1.4 随机森林回归模型验证

只有利用合适的评价指标才能准确验证模型的正确性，在随机森林模型中拟合优度R2以及均方根误差RMSE便可以作为较为合适的两个评价指标。拟合优度R2用于检验回归模型对样本数据的拟合程度，范围在0～1之间，取值越大，拟合程度越高；均方根误差RMSE用于表现样本的离散程度，是估计量预测值与实际观测值之间相差绝对值的总和，统计数据越完美，那么均方根误差RMSE的值越接近0，但均方根误差RMSE大小同时还受预测数值的大小影响。两个评价指标的表达式如下：

(9)

(10)

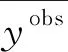
1.5 Pearson函数

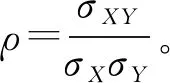
(11)

Pearson相关系数的主要作用是分析两个连续变量之间的相关关系。其取值范围是[-1,1]。样本相关系数r的绝对值表示两个连续变量间相关关系的强弱，绝对值越接近1，则两个连续变量相关程度越高，关系越密切。由于r是样本统计量，则抽样波动性会直接影响r的取值大小，所以两个变量之间线性关系是否显著可以由r进行统计分析进而判断。为了更加形象地表现出不同影响因素与混凝土碳化深度的相关性，可以采用相关性矩阵图来表示。

2 随机森林回归模型的建立

随机森林回归模型对于影响因素重要性的排序以及影响因素对评价指标的预测有重要意义，模型的实现主要包括如下几个步骤，如图1所示。

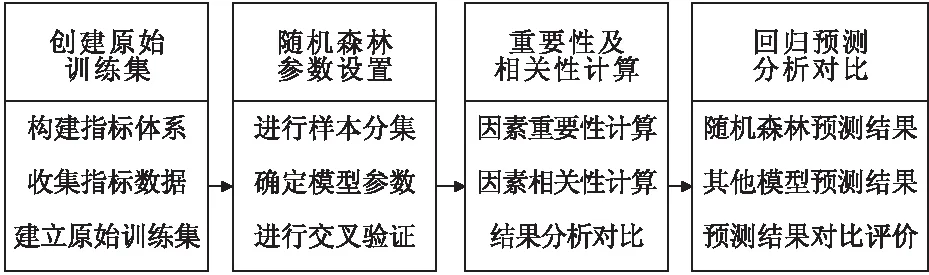
图1 随机森林回归流程

2.1 构建原始训练集

(1)构建指标体系。通过查阅大量相关文献以及工程实践材料，确定主要影响因素，从而构建指标体系。

(2)收集指标数据。在确定主要研究影响因素时，根据工程项目检测实验收集相关数据。

(3)建立原始训练集。根据工程项目检测实验收集的相关数据，建立原始训练集。

2.2 随机森林参数设置

(1)确定样本分集及模型参数

若样本数据比较小，为了使结果更加可靠，可将原始样本划分成训练集和测试集。具体步骤如下：

1)将原始数据随机分为K组，利用其中一组数据子集中的数据分别做一次测试集用来测试模型；

2)将余下的K-1组子集作为训练集用来训练模型，那么总共可以得到K个模型；

3)用得到的K个模型预测精度的平均值作为这个模型预测精度的最终估计值，最优的训练模型为其中预测精度最高的模型。

(2)交叉验证

在随机森林模型的建模流程中，主要参数有两个，分别为：随机森林树的棵数ntree、模型中所挑选的变量数mtry。设数据集中的变量有P个，默认情况下随机森林分类模型中mtry=P，ntree=500；随机森林回归模型中mtry=P/3，ntree=500。

2.3 重要性与相关性计算

(1)因素重要性计算

由于随机森林具有能够计算单个特征变量重要性的特点[13]，对于已经生成的随机森林，若用袋外数据测试其性能，假设袋外数据总数为M,用这M个袋外数据作为输入，带进之前已经生成的随机森林分类器，分类器会给出M个相应的数据分类，因为这M条数据的类型是已知的，则用正确的分类与随机森林分类器的结果进行比较，统计随机森林分类器分类错误的数目，设为N，则袋外数据误差大小为：

(12)

随机森林中每一棵树的袋外数据误差记为errOOB1，将噪声干扰随机加入到袋外数据OOB的所有样本当中，重复计算其袋外数据误差，记为errOOB2。根据式(8)对不同影响因素进行重要性评分，并将这些重要性评分进行可视化绘图，使不同影响因素的重要程度更加清晰明确。

(2)因素相关性计算

为了进一步验证随机森林模型在此试验的准确度，可以利用Pearson函数模型分析不同影响因素与早期碳化深度的相关度，相关度程度由Pearson相关系数r大小表示，其值可根据式(11)求得。

(3)结果对比分析

将重要性的计算结果与相关性的计算结果进行对比分析，可进一步确认随机森林预测模型的准确性。

2.4 回归预测对比评价

(1)随机森林预测结果

R语言软件[14]是一种自由软件编程语言与操作环境，是一种数学计算的环境，是一套完整的数据处理、计算和制图软件系统，具备高效的数据处理和存储功能。本文利用R语言软件，在调用随机森林算法程序包的基础上，编写与数据处理相关的R语言代码，就可以实现碳化深度随机森林预测模型的计算。

(2)其他预测模型

为了进行对比分析，本文选择准确程度相对较高的BP人工神经网络以及小波神经网络进行建模并预测分析。

(3)预测结果对比分析

选用均方误差MSE、拟合优度R2等参数来判断模型的预测精度，计算公式参考式(9)(10)，将三种预测模型误差进行对比分析。

3 案例分析

3.1 工程背景

松原至通榆段高速公路项目是《国家公路网规划》中绥芬河至满洲里高速公路铁力至科右中旗联络线的组成部分，也是《吉林省省级公路网规划》 “五主、一并、一环、七联络”中“联三”线的组成部分，在国家级和区域级公路网中均有重要意义。松通高速以松原市的前郭县为起点，途中经过乾安县后进入白城市境内，再经通榆县，最后以吉林省白城市通榆县与内蒙古自治区科右中旗交界处(吉、蒙省界)为终点。本文所获取影响因素相关数据样本来自松通项目的多个标段。

3.2 构建原始训练集

(1)建立指标体系

基于大量工程实践和文献可知[15～19]，混凝土的早期碳化性质与原材料组成成分以及组成成分的比例有关，因此本文将主要从材料层面选择影响混凝土早期碳化的影响因素，具体因素包括：水泥强度、水泥用量、粉煤灰用量、细集料用量、粗集料用量、混凝土强度、硅灰用量、水胶比、平均粒径等。评价碳化性评价指标确定为碳化深度。

(2)建立原始训练集样本数据

以松通项目土建工程混凝土碳化深度作为混凝土碳化性的输出变量。选取检测的36组数据作为原始训练集，部分数据如表1所示。

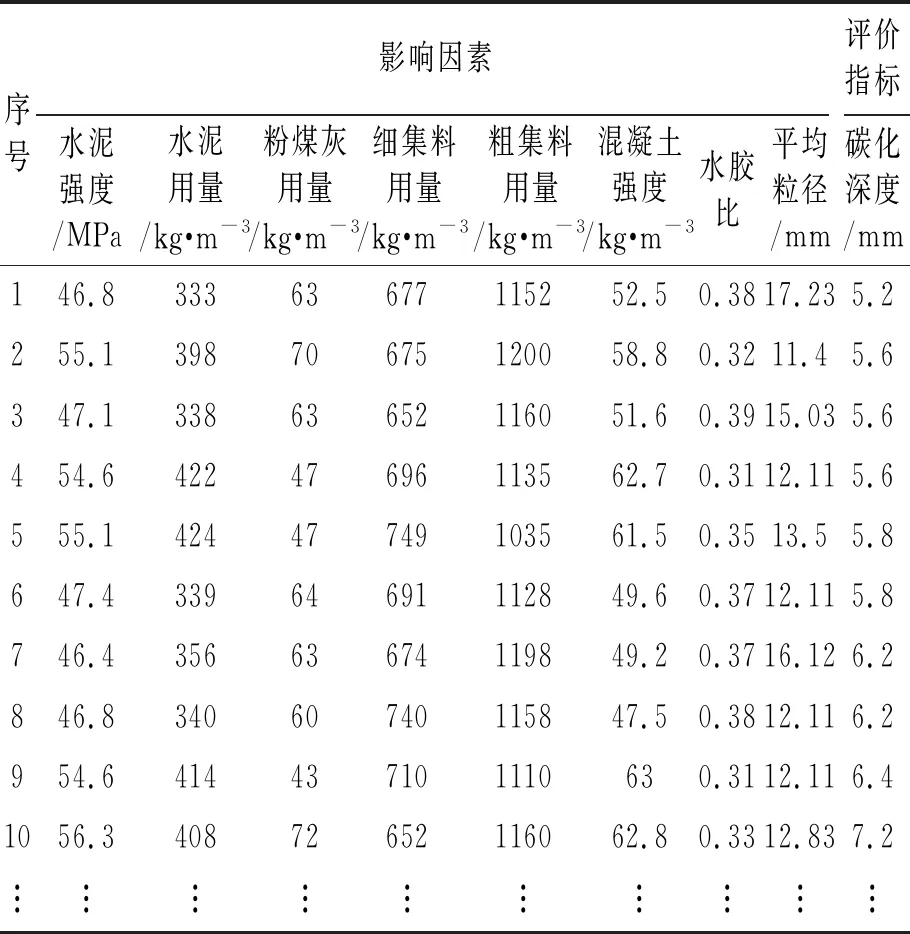
表1 工程实测样本数据

3.3 随机森林模型建立

(1)样本分集

先将上述选取的监测样本随机分为 5等份，任选其中4份作为样本训练集，其作用是确定随机森林参数和构建随机森林模型，另外1份作为样本测试集用于模型预测好坏性能的评估，同时强调后文中所出现的原始训练集以及原始测试集即为此处所提及的训练集和测试集。

(2)交叉验证

默认情况下mtry=P(分类模型)或mtry=P/3(回归模型)；ntree=500。Breiman的研究指出：当随机森林的参数取默认值时，模型往往也能取得比较理想的效果。因此本文将取mtry=P/3，ntree=500建立回归模型，以此保证准确度。

(3)重要性计算

通过随机森林回归模型分析各个影响因素对早期碳化深度的重要性程度，同时将重要性程度大小按照降序方式进行排列，节点纯度(InNodePurity)的变化幅度越大，说明该影响因素越重要，表2为重要性排序表。由重要性排序及得分可知，平均粒径、水胶比、水泥用量、混凝土强度、细集料用量等变量重要性度量值相对较大。

表2 重要性排序

(4)相关性计算

利用Pearson函数可以分析各个影响因素之间以及影响因素与早期碳化深度之间的相关性，可以作为对随机森林回归模型预测结果的一种验证手段，计算结果的相关性图如图2所示。在相关性图中，蓝色代表影响因素与碳化深度呈正相关，而红色则呈负相关，圆形半径越大代表影响因素与碳化深度的相关性越强，半径越小则相关性越弱，由这几点可以看出，平均粒径、水胶比、水泥用量、混凝土强度、细骨料用量与碳化深度的相关性明显高于其他影响因素，且与重要性排序图大体一致，进一步说明这些影响因素是对碳化深度性能有较大影响。

由于数据来源项目实际工程，表明这些因素是本项目混凝土早期碳化主要影响因素，工作中要加强这些因素的管控。

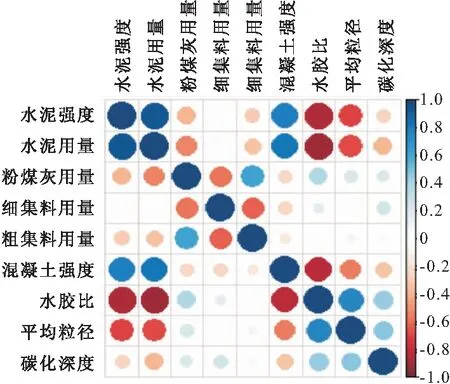
图2 因素相关性

(5)模型训练及预测

通过随机森林回归模型对训练样本进行拟合，对测试样本的预测结果如图3所示。

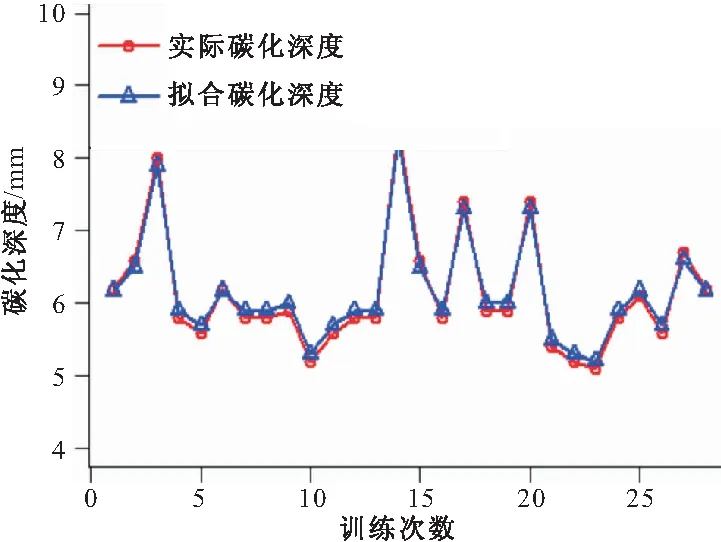
图3 训练集拟合结果

从图3可以看出，早期碳化程度拟合值和实际值比较接近，模拟效果较好。同时对测试集进行预测检验，如图4所示，可以看出测试集预测结果的预测值曲线与实际值曲线两者非常贴近。

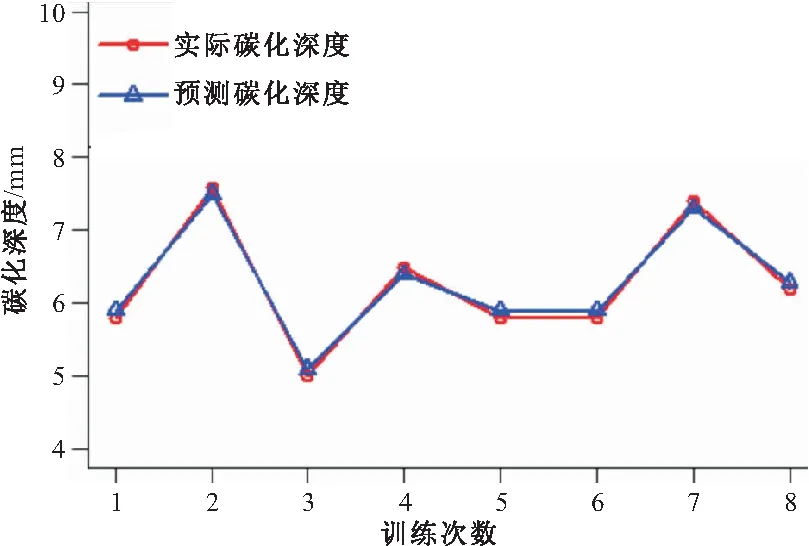
图4 测试集预测结果

3.4 回归预测结果对比分析

为了进一步检验基于随机森林模型(RF)预测早期碳化的优越性，便选择BP人工神经网络和小波神经网络进行对比分析，选用式(8)均方根误差和式(9)确定性系数两个系数来衡量不同预测模型的预测精度，通过比较这三个预测模型所得到的两个系数来确定精确程度，得到误差结果对比结果，如表3所示。

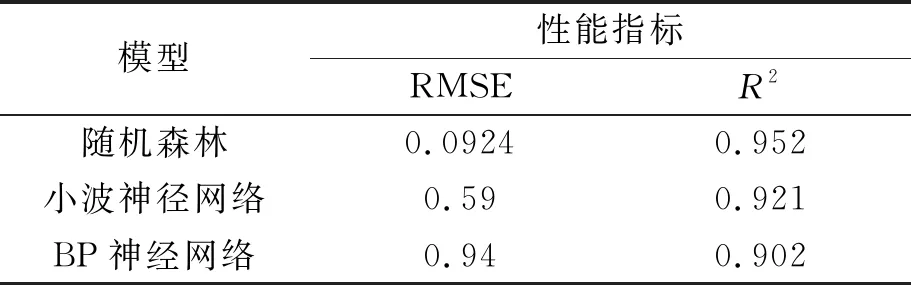
表3 误差比较

从预测结果对比表可以得出：随机森林预测模型、BP人工神经网络预测模型、小波神经网络分析的均方根误差分别为0.00057，0.016，0.0138，确定性系数分别为0.694，0.734，0.5433，可以看出在确定性系数十分相近的前提下，由随机森林模型得出的均方根误差远远小于由人工神经模型以及小波神经网络模型得出的均方根误差，说明随机森林模型预测结果最为贴近实际值，精度更高，效果更好。

4 结 论

(1)利用随机森林回归模型预测混凝土的早期碳化程度，通过此预测模型得到所选影响因素对于早期碳化深度的重要性程度，并且得出了效果比较好的预测结果。这证明所提出的随机森林预测模型为实现碳化深度预测提供了一种有效的工具。

(2)本文以松通项目为研究案例，根据混凝土的早期碳化程度与原材料性质选择了9个相关的影响因素，并利用Pearson函数得到了在这些影响因素相关性程度，其中平均粒径、水胶比、水泥用量、混凝土强度、细集料用料量等变量重要性度量值相对比较大，与碳化深度的相关性明显高于其他影响因素，由于数据来源实际工程项目，表明要加强这些因素的管控。

(3)本试验将随机森林模型的误差与人工神经网络模型以及小波神经网络分析的误差计算结果进行对比分析。结果表明，与BP人工神经网络预测模型以及小波神经网络预测模型相比，随机森林预测回归模型所得到的预测结果更为准确和稳定，从而进一步说明了随机森林预测模型在对混凝土早期碳化程度的研究中具有更大的优势。