基于相关性与关联规则一致性的中考成绩分析方法研究

任福栋，孙菲，任福捷，郭悦，刘宁

基于相关性与关联规则一致性的中考成绩分析方法研究

任福栋1，孙菲2，任福捷3，郭悦1，刘宁1

（1. 齐齐哈尔市招生考试院，黑龙江 齐齐哈尔 161006；2. 齐齐哈尔高等师范专科学校 职业技术系，黑龙江 齐齐哈尔 161005；3. 讷河市拉哈一中，黑龙江 讷河 161300）

选取齐齐哈尔市2019年市区中考成绩，在市级、区级、校级3个层面上进行学科间数据分析．计算关联规则数据中的学科相关系数，验证关联规则与学科相关系数是否具有一致性，进行中考成绩评价分析，找出学科间存在的相互影响关系，为提高薄弱学科成绩提供参考与借鉴．

相关系数；关联规则；中考成绩；齐齐哈尔市

相关性分析是指对2个或多个具备相关性的变量元素进行分析，从而衡量2个变量因素的相关密切程度[1-5]．相关性不等于因果性，也不是简单的个性化，相关性所涵盖的范围和领域几乎覆盖了我们所见到的方方面面[6-10]．在学科成绩相关性分析中，计算学科间的相关系数，可以检验学科间的相关性显著程度[11]，能够验证两两学科间的相互影响情况，反映学科间整体影响情况；关联规则分析，可以检验各学科分段间是否存在关联关系[12]，并通过关联前项得出所影响的关联后项，关联分析中的关联前项与关联后项反映出学科各分段的影响情况[13]，即学科局部影响情况．因此，相关性分析与关联规则二者都能够反映学科间相互影响关系，将二者相结合，通过对选定关联规则中的数据计算学科相关系数，验证学科间影响是否具有一致性，将能够从整体和局部2个方面共同检验学科间的影响情况．

本文选取齐齐哈尔市2019年市区中考成绩，在市级、区级、校级3个层面进行相关性与关联规则成绩数据分析，验证关联规则是否符合学科间的相互影响关系，以此确定学科间的影响规则，提出通过同步加强相关学科教学的方式改进薄弱学科成绩的方法，为提高薄弱学科成绩提供参考与借鉴．

1 相关性与关联规则一致性的中考成绩分析方法

1.1 相关系数确定学科整体相关程度

利用皮尔逊积差相关系数法[14]，能够计算2个变量间的简单相关系数，相关系数数值的绝对值越大，说明2个变量相关程度越紧密；相关系数数值的绝对值越小，说明2个变量相关程度越不紧密[15]．相关系数的正负符号代表2个变量的相关方向性，即相关系数为正数时，代表2个变量正相关，相关系数为负数时，代表2个变量负相关[16]．皮尔逊积差相关系数计算公式为

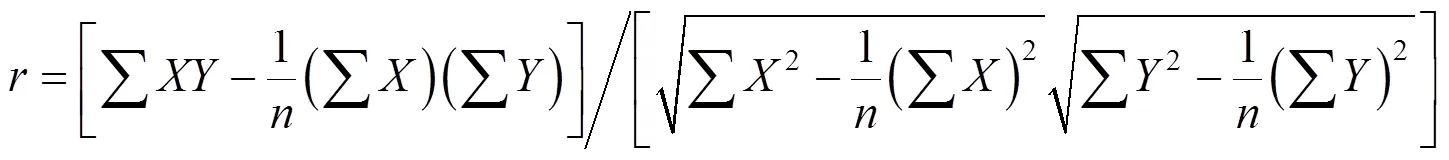
通过计算中考各学科间简单相关系数，对学科间简单相关系数进行分析，可以确定学科间的整体相关程度，利用相关影响关系进行学科教学调整，有利于强化薄弱学科成绩的提高．

1.2 关联规则确定学科分段关联关系

利用关联规则Apriori算法[17]，对学科成绩数据进行高分段、中分段、低分段划分，进行布尔型数据转换[18]，设置最低条件支持度与最小规则置信度后，进行学科成绩数据分析，得出高于最低条件支持度和最小规则置信度的关联规则项[19]．对关联规则项集进行关联规则事项分析，获取关联规则前项推导出关联规则后项的关联规则，获得各学科高分段、中分段、底分段的前置影响条件和后置影响结果，得到学科局部间的影响规则．为加强薄弱学科各分段学生教学提供科学依据，有助于提高学科薄弱分段学生的成绩[20]．

1.3 相关性与关联规则一致性的中考成绩分析方法

将考查学科高分段、中分段、低分段间影响关系的关联规则与考查学科整体间影响关系的相关性分析相结合，能够更好地验证学科间的影响关系[21]．对中考各学科成绩按照满分值（语文、数学、英语满分值为120分，物理、化学、思品、历史满分值为100分）的80%和60%3个分数点选取分界点，将各学科成绩划分为高分段、中分段和低分段3个分段，即满分为120分的学科分界点为96分和72分，满分为100分的学科分界点为80分和60分．利用关联规则Apriori算法得出符合最低条件支持度与最小规则置信度的关联规则，选取其中某个规则，确定关联规则前项与关联规则后项．在中考成绩库中将关联规则前项和关联规则后项的分段数据进行筛选，建立新的学科成绩数据库．利用相关性分析方法对数据库中的学科成绩数据进行分析，计算数据库中学科间的简单相关系数，对学科间计算的简单相关系数值进行分析，确定关联规则分析结果与相关性分析结果是否具有一致性[22]．对经过相关系数验证，具有一致性的关联规则分析结果，确定其是可信的，能够确定学科影响关系符合中考成绩分析实际，这种关联规则可为改进教学提供参考和借鉴；对经过相关系数验证，关联规则与相关系数不具有一致性的关联规则分析结果，其具有不可信性，不能将其作为改进教学的参考规则，将其舍去[23]．

通过相关性分析验证关联规则的中考成绩分析方法，避免了关联规则偶发因素的影响，确保了经过2种方法检验的关联规则的可信度，保证了关联规则分析结果的可用性[24]．

2 相关性与关联规则一致性的中考成绩分析方法应用

本文利用2019年齐齐哈尔市中考市区7 901名（经剔除特殊值数据考生后，共为7 819名）考生成绩数据作为分析对象，利用SPSS公司SPSS Clementine 12.0数据挖掘软件中的Apriori数据分析模型进行关联规则分析．相关性分析利用Microsoft Visual FoxPro 6.0软件借助式（1）自行编程进行．在具体对象分析上，选取2019年齐齐哈尔市市区中考数据中的某一区、某一初中学校为分析对象，为避免数据量小影响分析结果的情况，选取数据对象都为1 000人以上的区、初中学校．

2.1 整体数据的关联规则分析与相关性分析

对全部7 819名考生数据进行关联规则分析和相关性分析，关联规则分析结果见图1，相关性分析结果见表1．

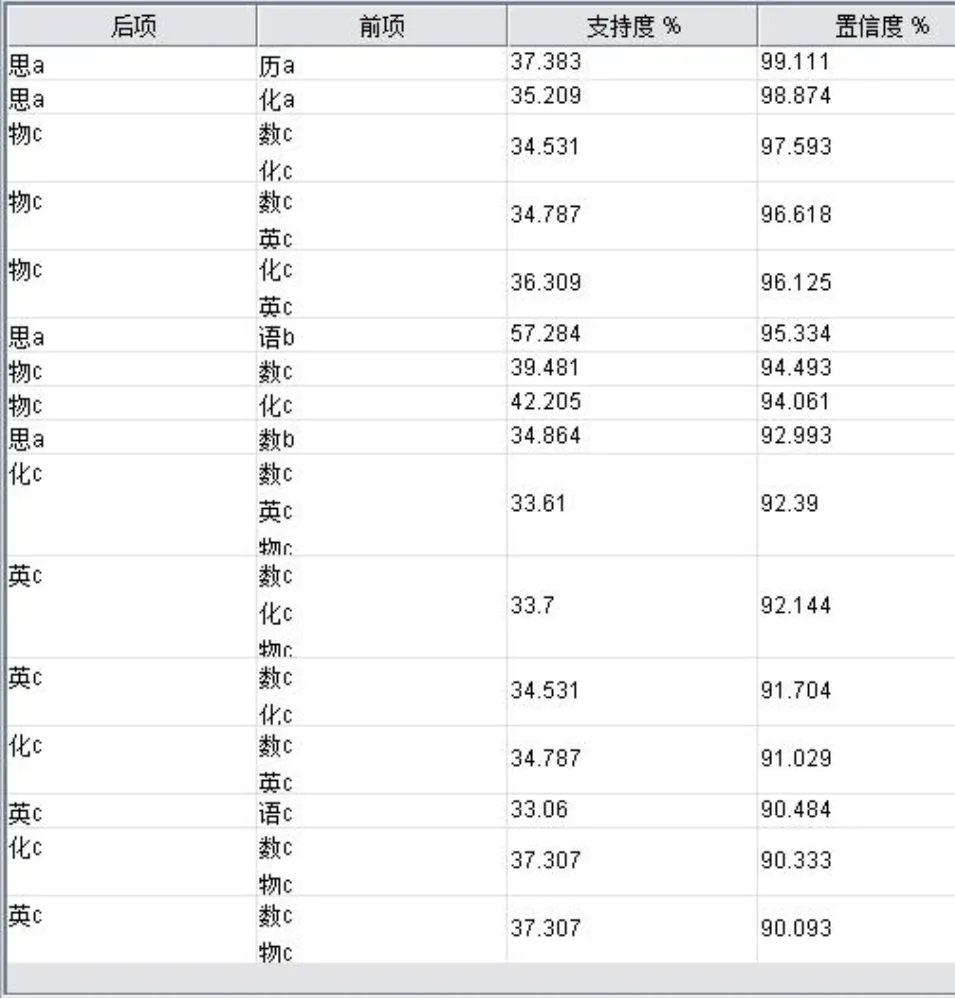
图1 市区考生数据关联规则分析

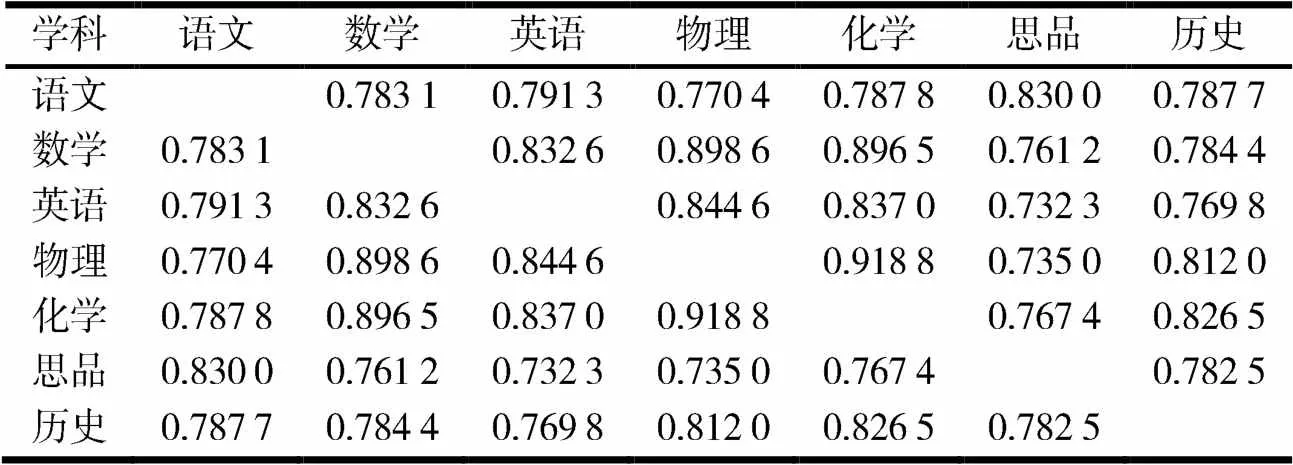
表1 市区中考各科相关系数

对选取的某区1 560名考生数据进行关联规则分析和相关性分析，关联规则分析结果见图2，相关性分析结果见表2．

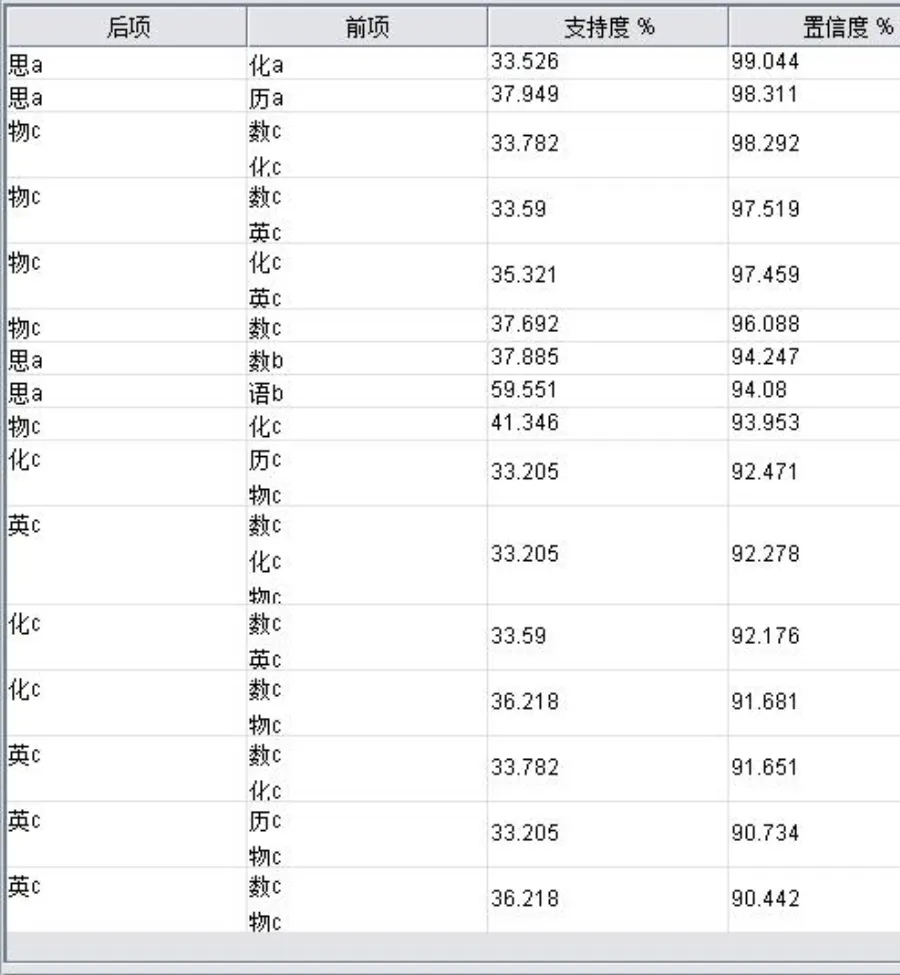
图2 某区考生数据关联规则分析

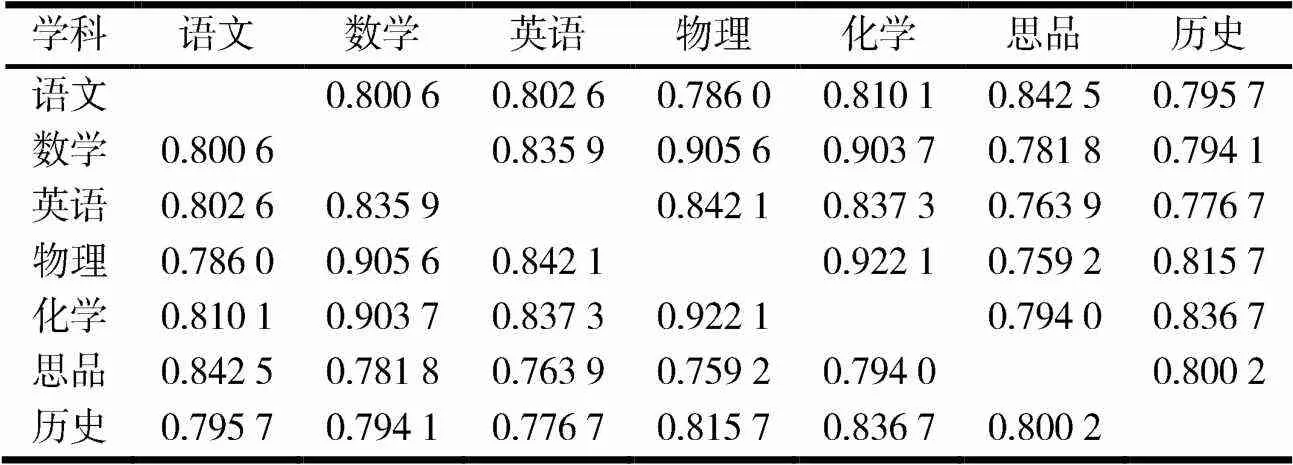
表2 某区中考各科相关系数

对选取的某初中学校1 026名考生数据进行关联规则分析和相关性分析，关联规则分析结果见图3，相关性分析结果见表3．

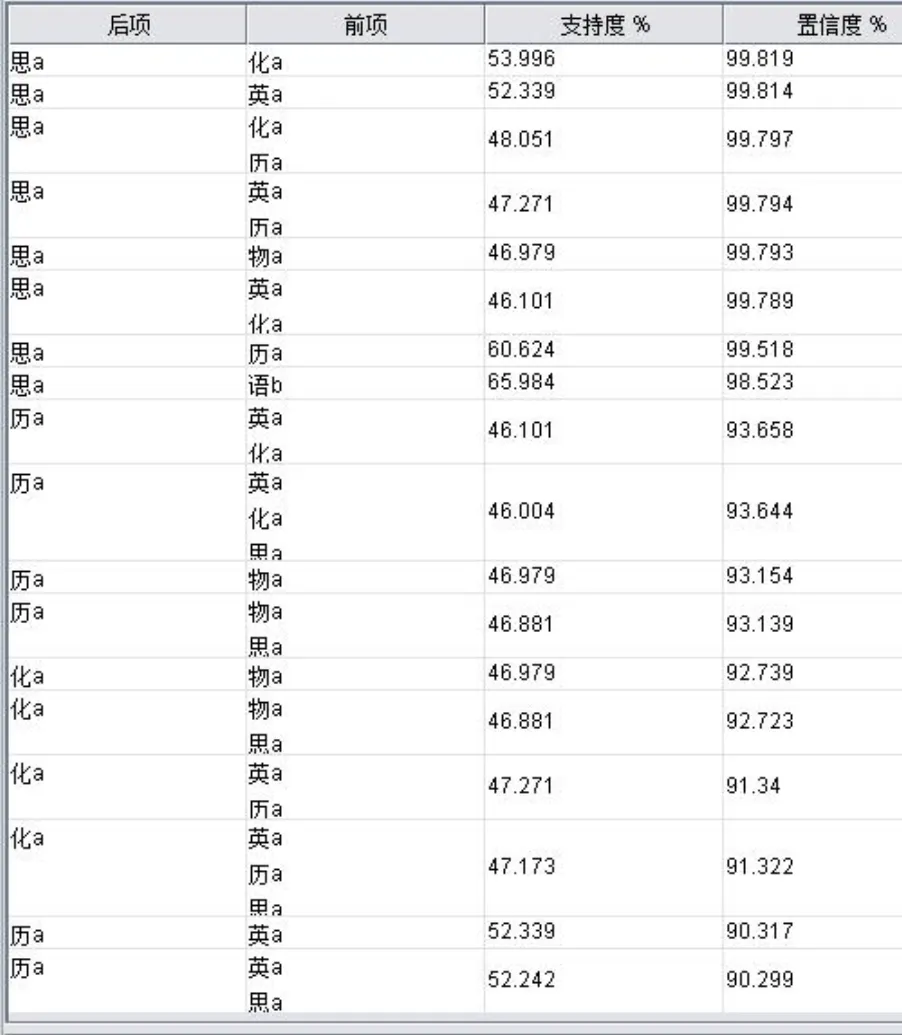
图3 某校考生数据关联规则分析

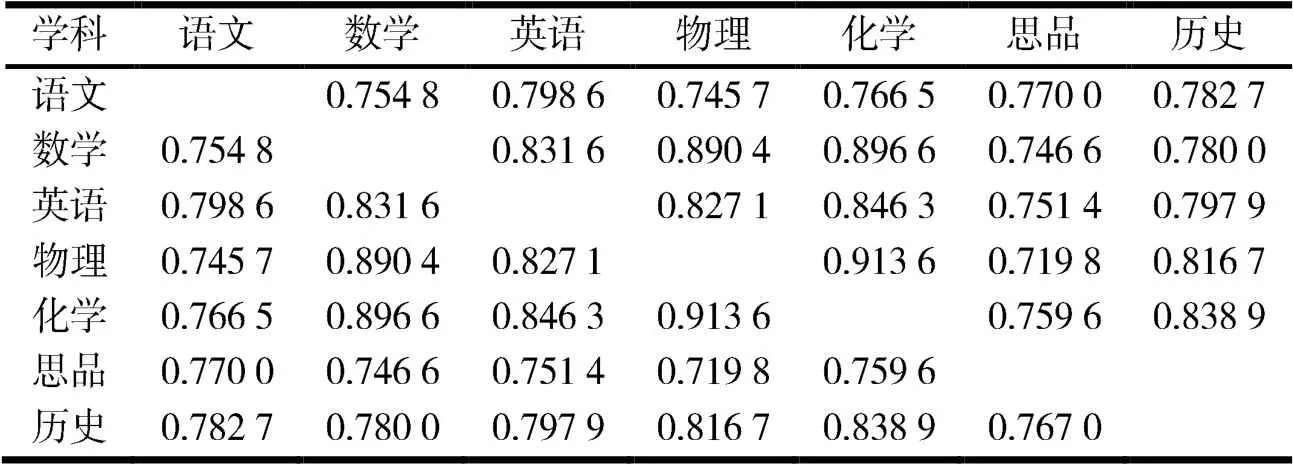
表3 某校中考各科相关系数

2.2 选取关联规则项进行相关性分析

对于图1全部考生数据关联规则分析结果，选取第3项关联规则，即关联前项数学c、化学c得出关联后项物理c，该关联规则的支持度为34.531%，置信度为97.593%．将该关联规则前项与后项2 635名考生数据建立新的成绩数据库，进行相关性分析，分析结果见表4．

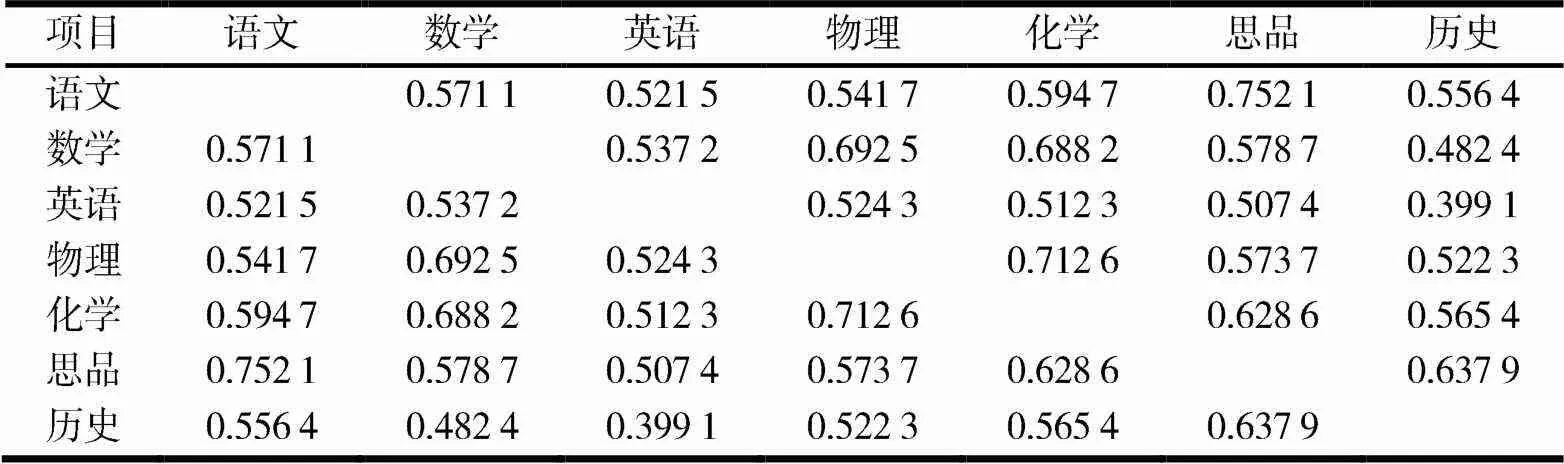
表4 市区数学c、物理c、化学c关联规则下中考各科相关系数

对于图2某区考生数据关联规则分析结果，选取第8项关联规则，即关联规则前项语文b得出关联后项思品a，该关联规则的支持度为59.551%，置信度为94.08%．将该关联规则前项与后项860名考生数据建立新的成绩数据库，进行相关性分析，结果见表5．

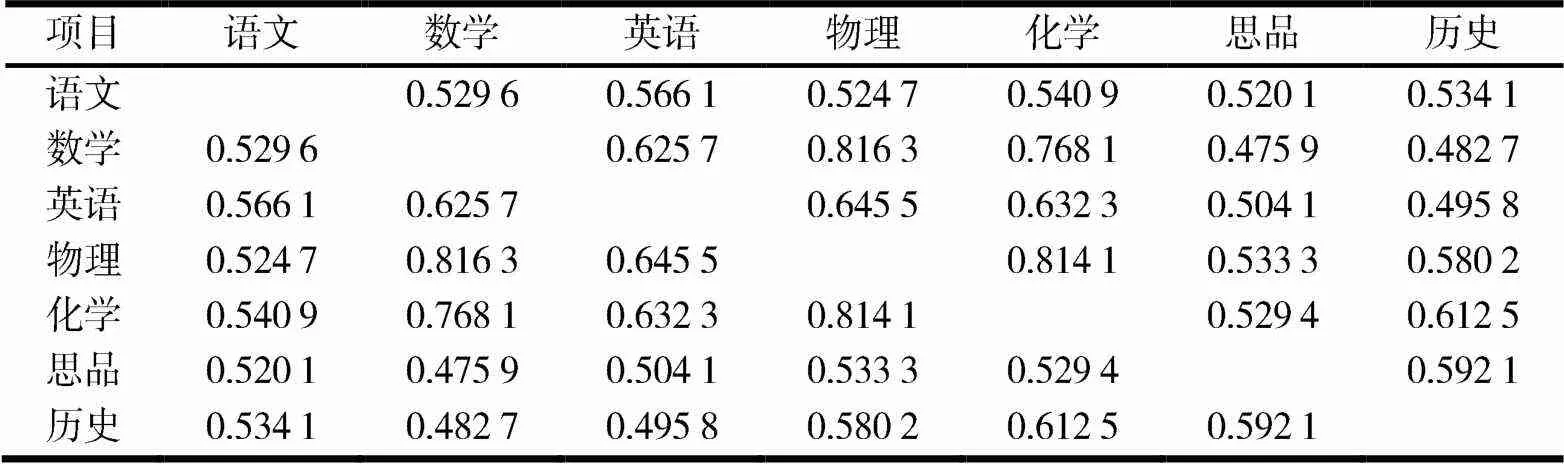
表5 某区语文b、思品a关联规则下中考各科相关系数

对于图3某初中学校考生数据关联规则分析结果，选取第13项关联规则，即关联规则前项物理a得出关联后项化学a，该关联规则的支持度为46.979%，置信度为92.739%．将该关联规则前项与后项447名考生数据建立新的成绩数据库，进行相关性分析，分析结果见表6．

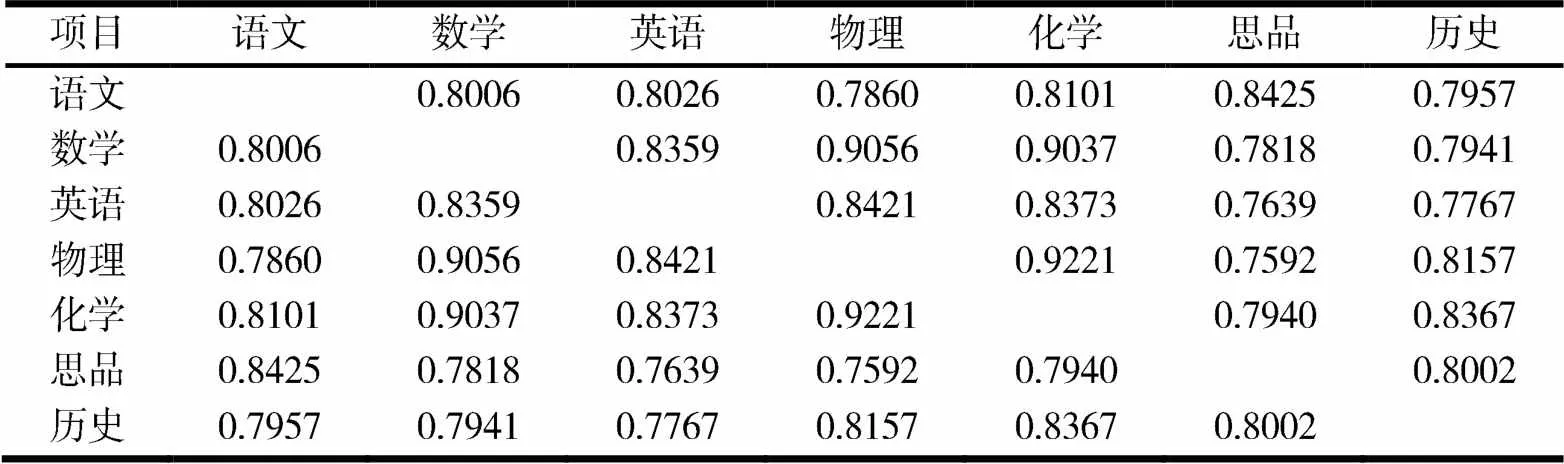
表6 某校物理a、化学a关联规则下中考各科相关系数

2.3 关联规则分析与相关性分析一致性检验

由表4可以看出，物理与数学的相关系数为0.692 5，物理与化学相关系数为0.712 6．在各学科间相关系数中，除去相关系数最高的语文与思品（相关系数为0.752 1）外，物理与化学的相关系数由高到低排在第２位，物理与数学的相关系数由高到低排在第３位．说明在该关联规则中，关联规则与相关系数是趋于一致的．

由表5可以看出，语文与思品的相关系数为0.520 1，在各学科间相关系数中，排在21个学科相关系数中的倒数第4位．说明在该关联规则中，关联规则与相关系数是不一致的．

由表6可以看出，物理与化学的相关系数为0.922 1，在各学科间相关系数表中，物理与化学的相关系数最高，在21个学科相关系数中排在第１位．说明在该关联规则中，关联规则与相关系数是趋于一致的．

3 数据分析结论

3.1 关联规则对比分析

关联规则支持度为包含该关联规则前项或后项的项集与全部非空项集的比值，在衡量高分段考生成绩中，支持度数值越大，说明包含该关联规则前项和后项的项集越多，高分段考生人数越多，也就越支持该关联规则符合学科关联情况，反映出的教学效果也就越好；在衡量低分段考生成绩中，支持度数值越大，说明低分段考生人数越多，反映出的教学效果越差[25]．在市区全部考生化学低分段得出物理低分段的第８项关联规则中，支持度为42.205%，在某区考生化学低分段得出物理低分段的第９项关联规则中，支持度为41.346%，比市区全部考生该关联规则少0.859个百分点，说明在此关联规则下该区情况比市区情况好，物理低分段和化学低分段考生人数少，物理和化学学科教学效果较好．由于在学校分析中，选取的学校为初中热点校，学校考生成绩都较好，因此该校本身就不存在这种关联规则．在历史高分段得出思品高分段的关联规则中，市区全部考生、某区考生、某校考生都存在这种关联规则．市区全部考生的关联规则支持度为37.383%，某区考生的关联规则支持度为37.949%，某校考生的关联规则支持度为60.624%．这说明在该关联规则下所选取区的教学效果情况比市区全部的教学效果情况稍好一些，而所选取学校的教学效果情况比市区全部的教学效果情况和选取区的教学效果情况好很多，因此该校历史高分段学生和思品高分段学生教学效果非常理想．

3.2 关联规则分析与相关性分析一致性结果

通过对市区全部考生中考成绩、某区考生中考成绩、某校考生中考成绩３个层面考生中考成绩数据关联规则分析及关联规则下的考生中考成绩相关性分析，可以验证关联规则分析结果中的关联规则．有些关联规则的关联规则前项与关联规则后项中，关联项所在学科间的相关系数在所有学科间相关系数中是高的，即关联规则与关联前后项学科间相关系数是趋于一致的，说明关联规则符合成绩数据一致性变化趋势．

市区关联分析中的数学低分段、化学低分段得出物理低分段的关联规则，该规则的支持度达到34.531%，置信度达到97.593%．说明数学成绩低并且化学成绩低的学生，物理学科成绩低的概率较大，数学低分段、化学低分段得出物理低分段规则项集占到所有非空项集的34.531%，即在低分段学生中数学成绩与化学成绩影响到物理成绩．对该相关规则下的2 635名学生进行学科相关系数分析，得出物理与数学的学科间相关系数为0.692 5，物理与化学学科间相关系数为0.712 6，在21个学科间相关系数中，除语文与思品学科间的相关系数最高外，物理与化学、物理与数学的学科间相关系数排在前2位．说明物理与数学、化学学科间相关关系非常显著，物理与数学、化学学科影响较为密切，也印证了关联规则中低分段学生物理成绩受到数学成绩和化学成绩的影响．这为改进学科教学提供了依据，要提高物理学科低分段学生的物理成绩，要同步对这部分学生数学成绩和化学成绩进行教学提高，受学科间相互影响的作用，通过数学、化学、物理3科同步进行加强教学，物理学科成绩提高的效果将更加显著；反之，在加强数学学科成绩偏低和化学学科成绩偏低的学生教学过程中，也可以带动学生物理学科成绩的提高．

某校考生关联分析中的关联前项物理高分段得出关联后项化学高分段的关联规则，该关联规则的支持度达到46.979%，置信度达到92.739%．说明物理学科成绩高的考生化学学科成绩高的概率较大，物理高分段得出化学高分段规则项集占到所有非空项集的46.979%，即在高分段考生中物理成绩影响到化学成绩．对该关联规则下的447名考生进行学科间相关系数分析，得出物理与化学学科间相关系数为0.922 1，在21个学科间相关系数中物理与化学的学科间相关系数最高，排在第１位．说明物理与化学学科间相关关系非常显著，学科间影响较为紧密，也充分印证了关联规则分析得出的物理高分段影响化学高分段的关联规则．这为高分段考生提高化学学科成绩提供了依据，要提高高分段考生化学成绩，应同步对这部分学生加强物理学科教学；反之，在加强高分段考生物理教学的同时，也能够带动考生化学成绩的提高．

3.3 与相关性分析存在差异性的关联规则假象

在关联规则分析结果中，有些关联规则的关联规则前项与关联规则后项中，关联规则前后项学科间相关系数在所有学科间相关系数中不突出，是低的或靠后的，即关联规则与关联前后项学科间相关系数是不一致的．说明这种关联规则不符合成绩数据相关关系变化趋势，其关联规则对表现学科间关联性不可信，这种关联规则所反映的情况不能应用于学科教学中，应该在分析结果中舍去，避免错误地影响学科教学的调整．如对某区数据分析得出，关联分析中的关联前项语文中分段得出关联后项思品高分段的关联规则，该规则的支持度达到59.551%，置信度达到94.08%，应该是较强的关联规则．将该关联规则中的860名考生学科成绩进行相关性分析得出，语文与思品学科间的相关系数仅为0.520 1，在21个学科间相关系数中排倒数第４位．说明在这860名考生成绩中，语文学科与思品学科相关性不显著，即语文中分段关联前项得出思品高分段关联后项的关联规则与相关性分析结论不一致，此关联规则存在关联规则假象问题，不能将其作为改进教学的依据应用到教学中．

4 结语

通过对中考考生成绩进行相关性与关联规则一致性检验，可以利用相关系数表现学科间变化情况的功能验证关联规则可信性，确定符合成绩数据实际情况的关联规则，并将可信的关联规则应用于教学过程中．针对关联规则具体情况同步制定提高学科教学质量的措施，从而改进学科教学，提高学科成绩．规避了关联规则假象的问题，避免由于过度信任关联规则而制定错误的改进教学措施的情况发生．这种利用相关系数验证关联规则的方法，在实际应用中需要利用程序编制分析软件，实现理论研究转化为应用成果，运用于实际成绩数据分析工作中．

[1] 贲维维．高一函数学习与中考数学成绩相关性分析及教学提升探索[D]．南京：南京师范大学，2018

[2] 宣筱潇，李琪．相关关系分析法在多学期数学成绩相关性中的应用[J]．科教导刊（下旬），2019（1）：23-24

[3] 王孝玲．教育统计学[M]．4版．上海：华东师范大学出版社，2008：197-203

[4] 薛薇．统计分析与SPSS的应用[M]．5版．北京：中国人民大学出版社，2017：185-194

[5] 吴飞青，吴成玉，方伟，等．基于数据挖掘的成绩相关性实证分析[J]．电气电子教学学报，2019，41（4）：1-3，13

[6] 张翼．解析图书情报分析中相关性分析原理的有效应用[J]．科技资讯，2019，17（22）：255-256

[7] 叶永明，魏奇龙，罗丽芳．胎儿颜面畸形超声检测的应用价值及其与染色体异常的相关性分析[J]．中国优生与遗传杂志，2019，27（7）：864-866

[8] 刘祥洁．水质自动监测参数的相关性分析及在水环境监测中的应用[J]．节能，2019，38（7）：78-79

[9] 王小兰，陈甲瑞，邢震，等．藏东南高山松胸径与冠径的相关性分析及应用研究[J]．林业资源管理，2019（1）：63-69

[10] 袁立霞，罗晓，张文丽，等．制药废水厂微生物群落和多种抗性基因相关性分析[J]．河北科技大学学报，2019，40（2）：175-181

[11] 陈小杭．高考数学成绩与大学数学专业课学习能力相关性分析[J]．长春教育学院学报，2019，35（2）：8-10

[12] 曾兴．基于关联规则挖掘的学生成绩分析研究[D]．海口：海南大学，2018

[13] 王成勇．基于关联规则Apriori算法的学生成绩分析[J]．价值工程，2018，37（5）：171-173

[14] 任福栋，任福捷，孙美琪，等．高考成绩相关性分析研究与应用[J]．齐齐哈尔师范高等专科学校学报，2019（4）：9-11

[15] 刘世欢．基于教育数据的相关性分析研究[D]．杭州：浙江工商大学，2018

[16] 周燚，严凤强，沈忠．贵州省高师体育专业学生专业学习与高考成绩的相关性分析[J]．体育科技，2018，39（1）：106-108

[17] 苗维诚，朱文婕．基于关联规则Apriori算法的物理实验成绩分析研究[J]．赤峰学院学报：自然科学版，2019，35（1）：14-16

[18] 吴小东，曾玉珠．基于Apriori算法的高校学生成绩数据挖掘[J]．廊坊师范学院学报：自然科学版，2019，19（1）：31-36

[19] 都娟．基于改进Apriori算法的成绩预警系统的研究[J]．西安铁路职业技术学院学报，2019（4）：33-38

[20] 马天昊，夏静，杨婧雅，等．基于Apriori算法的学生成绩关联规则挖掘[J]．现代职业教育，2019（27）：92-94

[21] 王咏梅．Apriori算法在学生成绩分析中的应用[J]．数字通信世界，2018（12）：177，181

[22] 杨宁．基于相关性分析的关联规则挖掘及其应用[D]．兰州：兰州大学，2019

[23] 邢晶晶．数据挖掘技术在成绩分析及课程设置中的应用研究[D]．兰州：兰州交通大学，2018

[24] 陈喜华，黄海宁，黄沛杰．基于Apriori算法的学生成绩分析在课程关联性的应用研究[J]．北京城市学院学报，2018（4）：60-65，84

[25] 郭鹏，蔡骋．基于聚类和关联算法的学生成绩挖掘与分析[J]．计算机工程与应用，2019，55（17）：169-179

Research on the analysis method of high school entrance examination scores from the perspective of relevance and consistency of association rules

REN Fudong1，SUN Fei2，REN Fujie3，GUO Yue1，LIU Ning1

（1.Qiqihar Enrollment Examination Authority，Qiqihar 161006，China；2. Department of Vocational Technology，Qiqihar Teachers College，Qiqihar 161005，China；3. Laha No.1 Middle School of Nehe City，Nehe 161300，China）

The scores of high school entrance examination of 2019 in urban areas of Qiqihar City are selected to carry out interdisciplinary data analysis at the three levels of city，district and school．The correlation coefficient of the discipline in the association rule data is calculated to verify whether the correlation rule is consistent with the correlation coefficient of the discipline for the evaluation analysis of high school entrance examination scores，with the purpose to find out the mutual influence relationship between disciplines and provide reference for improving the performance of weak discipline.

coefficient of correlation；association rule；high school entrance examination score；Qiqihar City

O29∶G633.6

A

10.3969/j.issn.1007-9831.2020.04.005

1007-9831（2020）04-0020-06

2019-12-04

黑龙江省教育学会科学研究规划“年度关注课题”（XHNY2018-105）——中考成绩相关性分析方法研究与实践

任福栋（1976-），男，黑龙江齐齐哈尔人，助理研究员，硕士，从事招生考试数据分析研究．E-mail：rfd_sf@163.com