基于数学史料的高中数学问题编制策略①
汪晓勤
(华东师范大学教师教育学院 200062)
1 引 言
近年来,随着HPM视角下课例研究的深入开展以及一系列相关课例的发表,越来越多的数学教师开始关注HPM的教学理念、教育价值和教学策略.一般说来,数学教学中运用数学史料的方式有附加式、复制式、顺应式和重构式[1].除了附加式(介绍数学家的生平轶事、提供数学史阅读材料等)外,其他三种方式都与问题提出息息相关:复制式指的原始材料的直接采用(有时需要进行必要的语言转换),其中最主要的材料之一就是历史上的数学问题;顺应式指的是对数学史料的改编,包括对问题的改编;重构式是指借助一系列由易至难、环环相扣的问题串,再现知识的发生和发展过程.因此,在HPM视角下的数学教学中,数学问题乃是数学史的最重要的载体.
另一方面,近年来,高考数学卷中相继出现了一些涉及数学文化的问题,这些问题引起人们的浓厚兴趣,已有大量文献对这些问题做过分析(如[5-11]).数学史是数学文化的重要组成部分,讨论高考数学文化题,都绕不开基于数学史的问题.尽管已有部分文献对数学文化或数学史问题进行了分类(如[6]和[8]),但分类方法还有待于进一步论证、细化和修正.本文的研究问题是:如何从数学史料出发,编制数学问题?高考数学卷中涉及数学史的问题反映了问题提出的哪些策略?
我们希望在已有相关研究的基础上,建立“基于数学史的问题提出策略”的分类框架,并用于部分高考试题以及高中数学典型问题的分析,为未来HPM视角下的课堂教学和试题命制提供参考.
2 基于数学史料的问题提出策略
美国学者希尔佛(Silver)等人的研究表明,根据已知情境或已知问题提出新问题的具体策略有四种[2][3]:
其中前两种策略即为所谓的“否定属性”(what-if-not)策略.如果给定情境是含有条件和目标(或结论)的数学史材料(主要是数学命题和数学问题),那么相应地,“基于数学史料的问题提出策略”也包含上述四类,从数学史运用方式上说,这四种策略都属于顺应式.但是,希尔佛在其研究中所发现的问题提出策略,并不考虑课堂教学的需求,而本文所说的“基于数学史的问题提出策略”是服务于课堂教学的,因而有其特殊性.对于含有条件和目标(或结论)的数学史料来说,具体体现在以下几个方面:
对于不含条件或目标(或结论)的数学史料(主要是指概念定义、作图工具等),为了编制满足课堂教学需求的问题,需要设定条件或目标,此时的策略也属于“自由式策略”.
因此,“基于数学史料的问题提出策略”至少有七类,见表1.
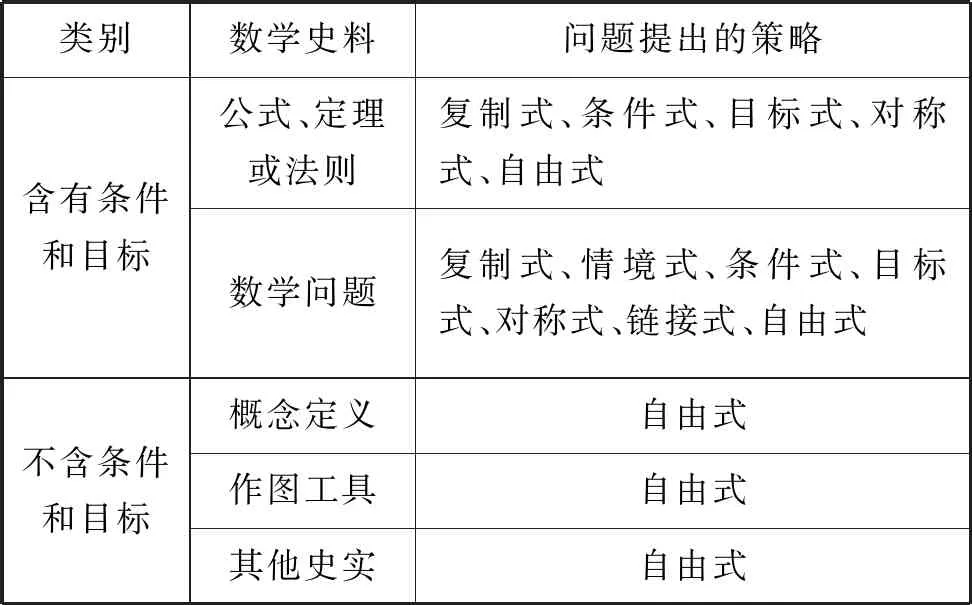
表1 基于数学史料的问题提出策略
例如,《九章算术》勾股章中设有如下问题(通常称为“勾股容方问题”):“今有勾五步,股十二步,问:勾中容方几何?”如果我们以该问题作为出发点,运用各种策略,分别可以提出以下新问题.
问题1:已知直角三角形的两条直角边的长分别为5和12,求与该直角三角形具有公共直角的内接正方形的边长.(复制式)
问题2:有一块直角三角形空地,直角边长分别为5米和12米.现要在该空地上建一个面积最大的正方形花坛,求该花坛的边长.(情境式)
问题3:已知直角三角形的两条直角边长分别为7米和25米,求与直角三角形具有公共直角的内接正方形的边长.(条件式)
问题4:已知直角三角形的直角边为a和b,求其内接正方形的边长.(条件式)

问题6:已知直角三角形的直角边为5和12,求其内接正方形的面积.(目标式)
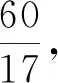
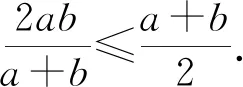
问题9:如图1,若Rt△ABC的两条直角边分别为a和b,正方形CEDF和MNPQ为它的两个不同的内接正方形,试比较ECFD和MNPQ边长的大小.(自由式)
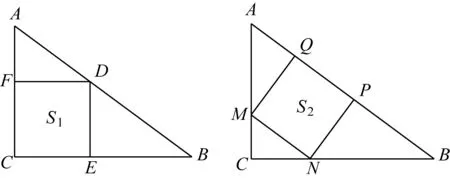
图1 勾股容方新问题
问题10:如图1,正方形CEDF和MNPQ内接于同一个直角三角形ABC,其面积分别S1和S2,A=α.已知S1=441,S2=440,求sin2α.(自由式)
3 基于数学史料的高考题
3.1 复制式问题
高考数学卷中的“复制式”问题较多取自中国古代数学名著《九章算术》和《数书九章》,如《九章算术》中的“九节均容”问题(2011年湖北文理卷)、“委米依垣”问题(2015年全国课标I卷)、《数书九章》中的“天池测雨”问题(2013年湖北文科卷)、“米谷粒分”问题(2015年湖北文理卷)等.2017全国II卷采用了明代数学家程大位(1533—1606)《算法统宗》中的问题:“远望巍巍塔七层,红光点点倍加增.共灯三百八十一,请问尖头几盏灯?”这是一道已由等比数列项数、公比与和求首项的问题.命题者除了对原文进行翻译外,原题的情境、已知条件和目标都不变,故属于“复制式”问题.
有些问题看似与数学史无关,但如果从数学史的角度去看,却是古代数学家解决过的问题.如2017年江苏卷中的一题:“如图(图2),在圆柱O1O2内有一个球O,该球与圆柱的上下底面及母线均相切.记圆柱O1O2的体积为V1,球O的体积为V2,则V1/V2的值是______.”该问题正是古希腊数学家阿基米德(Archimedes, 前287—前212)曾经孜孜以求的问题,问题的解决是阿基米德生前最引以为豪的工作,而在他去世之后,求与外切圆柱还被刻在他的墓碑上.因此,我们也可以将本题视为“复制式”问题.
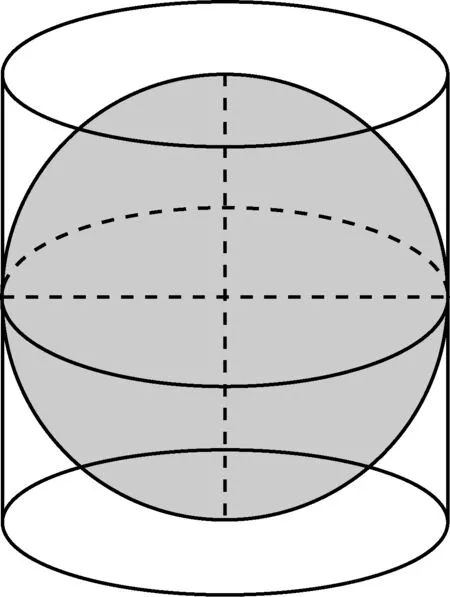
图2 圆柱及其内切球
3.2 条件式问题
2018年浙江数学卷根据《张丘建算经》中的百鸡问题编制了一道方程问题:
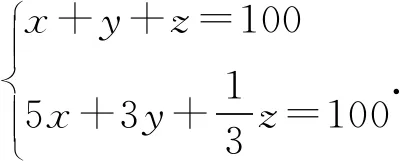
这里,命题者对“百鸡问题”中的条件进行操作,将原题中的不定方程组改编为一个适定的二元一次方程组,故属于“条件式”问题.
3.3 目标式问题
2017年浙江数学卷先介绍三国时代数学家刘徽的割圆术以及祖冲之的贡献,然后提出数学问题:我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度,祖冲之继承并发展了“割圆术”,将π的值精确到小数点后七位,其结果领先世界一千多年,“割圆术”的第一步是计算单位圆内接正六边形的面积S6,S6=______.
如图3所示,AB为圆内接正n边形的一边,长为an,AC=BC是圆内接正2n边形的一边,长为a2n,则圆内接2n边形的面积为
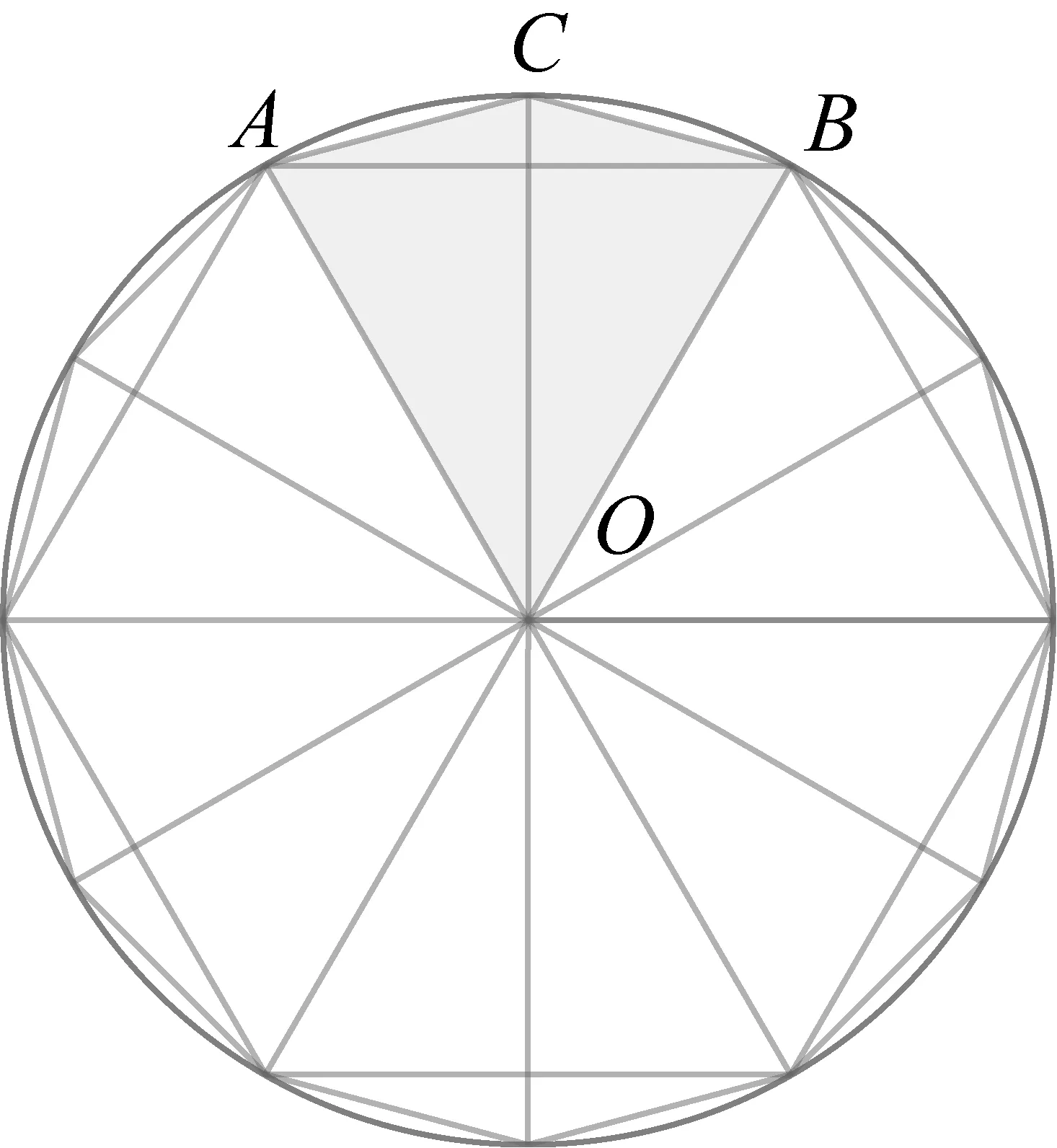
图3 割圆术
上述公式是割圆术的关键公式,刘徽利用该公式证明了圆面积公式.为了求圆周率的近似值,从a6=R=1尺出发,刘徽先计算出
再根据“倍边公式”
依次计算a12,a24,a48和a96,相应计算出
显然,割圆术的第一步不是计算S6,而是计算S12.因此,本题改变了割圆术中的目标,因而属于“目标式”问题.如果将所求项改为S12,那么问题就符合割圆术的原意,成为“复制式”问题了.本题中,命题者的初衷并非目标操作,但由于曲解史料的原意,无意中改变了问题提出的策略.
2018年全国I卷以希波克拉底定理为基础,编制了一道概率问题:
下图(图4)来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC和直角边AB,AC.ABC的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ.在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别为p1,p2,p3.则
A.p1=p2; B.p1=p3;
C.p2=p3; D.p1=p2+p3.
本题所依据的数学史料是希波克拉底定理,该定理的结论是Rt△ABC的面积等于两个弓月形面积之和,即区域Ⅰ的面积等于区域Ⅱ的面积.命题者对定理的结论进行操作,将Ⅰ和Ⅱ的面积关系替换为“在整个图形中随机取一点,此点取自Ⅰ和Ⅲ的概率p1和p2的大小关系”,形成一个新问题,故本题也属于目标式问题.

图4 希波克拉底的几何图形
3.4 自由式问题
“自由式”问题在历年高考题中也时有出现,如2012年湖北理科卷根据历史上圆周率的不同分数近似值,编制了一道比较包括《九章算术》“开立圆术”在内的不同球体积近似公式的问题;2015年湖北文理卷根据16世纪荷兰数学家舒腾(F. van Schooten, 1615—1660)的椭圆规编制的解析几何问题.2018年北京卷根据明代学者朱载堉(1532—1611)的“十二平均律”编制了一道等比数列问题:
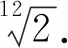
由于“十二平均律”属于音乐理论,属于表1中“不含条件和目标”的史料,由此提出的问题归为“自由式”.
当然,有些高考题虽然贴上了数学史的“标签”,但并不属于“基于数学史料的数学问题”.如2019年浙江数学卷先介绍了祖暅原理——“缘幂势既同,则积不容异”,然后编制了一道已知柱体的三视图,求柱体体积的问题.该问题本质上与祖暅原理并无多大关联.
4 基于数学史的数学问题举例
为了进一步说明“基于数学史的问题提出策略”的分类框架的可行性,我们再举两个例子.
4.1 奇数与立方数的关系
公元1世纪,古希腊数学家尼可麦丘(Nicomachus)发现奇数与立方数之间存在如下关系[12]:
1=13,
3+5=23,
7+9+11=33,
13+15+17+19=43,
…………………………
在尼可麦丘所生活的时代,人们并不会用字母表示数,因此,我们无法苛求他给出奇数与立方数的一般关系式.上述规律为三次幂和公式的发现开辟了道路,我们有理由相信,尼可麦丘已知道三次幂和的规律,因为同时代的罗马土地测量员据说都知道这个规律.事实上,根据尼可麦丘的上述规律,我们有
13=1=12(1个奇数),
13+23=1+3+5=(1+2)2(1+2个奇数之和),
13+23+33=1+3+…+11=(1+2+3)2(1+2+3个奇数之和),
13+23+33+43=1+3+…+19=(1+2+3+4)2(1+2+3+4个奇数之和),
……………………………
尼可麦丘写不出一般的等式,而有了字母表示任意数的思想,我们可以写出一般关系式,并找出更多的规律.据此,我们可以编制一系列问题.把正奇数数列{2n-1}中的数按上小下大、左小右大的原则排成如下三角形数表:

设anm(n,m∈N*)是位于该三角形数表中从上往下数第n行、从左往右数第m个数.
(1)用n和m表示anm;
(2)已知anm=2021,求n和m的值;
(3)设an1+an2+…+ann=bn,求数列{bn}的前n项和Sn;
(4)设cn=bn+1-bn,利用数列{cn}的前n项之和,求二次幂和12+22+…+n2;
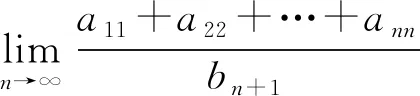
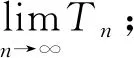
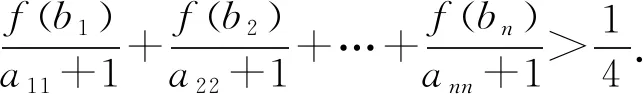
以上问题都是以尼可麦丘所发现的奇数与立方数之间关系为出发点,且问题的条件和目标都是新设的,因而均属于“自由式”问题.
问题(4)和(6)的背后还蕴含了更多的数学史元素.(4)中的累加法,正是17世纪法国数学家帕斯卡(B. Pascal, 1623-1662)推导幂和公式的方法,由等式
(r+1)p+1-rp
分别取r= 1,2,…,n,将n个等式两边分别累加,即可有p-1次以及更低次的幂和公式推导出p次幂和公式[13].
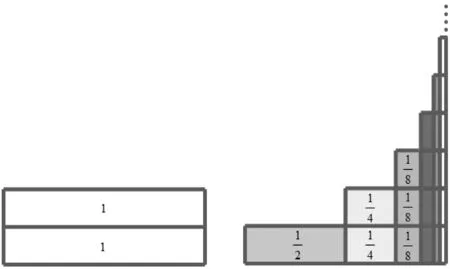
图5 奥雷姆的面积变换方法
从例1可见,从古代数学史料出发可以提出有若干问题组成的问题串,而其中的某些问题本身也可能是历史上别的数学家曾经解决过的问题,因次,如果以别的史料为参照,这些问题可能又会成为“复制式”或“条件式”问题了.
4.2 抛物弓形的面积
古希腊数学家阿基米德在其《抛物弓形求积》中解决了抛物弓形的面积问题.如图6所示,设AB是抛物线的一条弦,阿基米德证明[14]:

图6 抛物弓形的性质
命题1:过抛物线上任意一点P作抛物线对称轴的平行线,交AB与C,若AB平行于抛物线在点P处的切线MN,则AC=BC;反之,若AC=BC,则AB平行于抛物线在点P处的切线MN.
命题2:P为抛物线上任意一点,直线AB与抛物线在P处的切线MN平行,交抛物线于点A和B,过P作抛物线对称轴的平行线,交AB于点C,交抛物线在点A处的切线于点T,则PT=PC.
命题3:过AB的中点C作抛物线对称轴的平行线,交抛物线于点P,则P为抛物弓形的顶点.

由于只有纯几何的方法,加上没有极限概念,命题5的证明并非易事,需要用到穷竭法.而我们今天有了解析几何这一重要工具,再加上极限工具,可以根据阿基米德上述命题编制一组新的解析几何问题.
如图7,直线l:y=kx+b与抛物线x2=2py(p>0)相交于不同的两点A(x1,y1) ,B(x2,y2).M(x0,y0)是抛物线上任意一点,过M作y轴的平行线,交AB于C.

图7 基于数学史的抛物线问题
(1)求抛物线平行弦的中点轨迹;
(2)求抛物线在点M处的切线方程;
(3)证明:C是AB中点的充要条件是抛物线在点M处的切线平行于AB;
(4)证明:若C是AB的中点,且抛物线在点A处的切线与CM的延长线交于点T,则CM=MT;
(5)证明:若C是AB的中点,则CM是抛物弓形中所有与y轴平行的截线段中最长的线段,即点M是抛物弓形的顶点.
(6)设C为AB的中点,|x2-x1|=d,试用d来表示△ABM的面积.

(8)求抛物线弓形ABM的面积.
以上8个问题中,问题(3)、(4)、(5)、(7)和(8)分别对应于阿基米德的命题1-5,问题的目标没有变,但采用代数方程来表征抛物线和直线,问题的条件发生了改变,因此,这些问题都属于“条件式”问题.而问题(1)、(2)和(6)则属于“自由式”问题.
5 结 语
以上我们看到,根据“基于数学史料的问题提出策略”的分类,有关高考题大多采用了复制式、条件式、目标式和自由式四种,但很少采用情境式、对称式和链接式.根据“奇数与立方数之间的关系”和“抛物弓形的面积”两则史料所编制的一系列高中数学问题表明,由于古今数学表征、数学方法、数学工具的巨大差异,要编制适合于今日课堂教学或考试的数学问题,条件式和自由式往往是理想的选择.
基于数学史料的数学问题提出策略对于HPM视角下数学教学设计和数学文化试题的编制都有重要指导意义.但是,就像一个具有高超的烹饪技术但缺少好食材的厨师很难烧出一道好菜一样,一个掌握了问题提出策略却缺乏好素材的教师或命题者也无法编出一道好题.首先,一线教师和命题者需要针对高中数学课程中涉及的知识点开展更深入、系统的历史研究,丰富课程、教材和教学的数学问题资源;其次,教师专业发展指导者可将“基于数学史的问题提出”这一主题纳入在职教师的培训课程中,让一线教师更多地了解问题提出策略,学习如何对数学史料做出必要的裁剪和加工,形成合适的数学问题;再次,一线教师和命题者需要正确认识基于数学史料的问题的教育价值,不能仅仅满足于数学文化标签,而是要展示数学文化的精髓,充分发挥数学史的多元教育价值.

