基于SIMPACK和ABAQUS的青藏铁路既有列车提速动力分析

王鹏然，韩 峰

(兰州交通大学土木工程学院,兰州 730070)

青藏线格拉段全长1 142 km，为中国平均海拔4 000 m的高海拔地区及常年冻土区段，部分区段能力利用率趋于饱和。目前，青藏铁路格拉段为了适应铁路现代化发展的趋势，已经完成了扩能改造，这也就需要提高列车的运行速度以及列车的运行稳定性。因此对列车与线路之间的动力学性能进行研究分析对铁路运输的经济效益以及工程应用都有重要的意义。宁明哲等[1]运用MATLAB提出了一种既有线提速时缓和曲线长度的优化算法；刘鑫等[2]通过NUCARS对两种缓和曲线线型进行研究，认为采用三次抛物线型缓和曲线对列车提速是更为可行的；石万新[3]通过分析线路纵断面与平面的关系，对坡度减缓进行改造以及改变竖曲线半径和坡段长度进而实现对既有线的改造。李卫强等[4]通过调整曲线半径，分析机车在不同条件下的动力性能，得到了提速到200 km/h的曲线半径。高健等[5]通过改变列车运行方式、超高布设形式、缓和曲线线型及长度提出适应小半径曲线群的提速方案。

多体动力学分析软件SIMPACK，其轮轨接触方式为滚动接触，可以对轨道车辆的动力学性能进行更贴近实际的仿真[6]；ABAQUS作为一款有限元软件，在求解模型应力与位移方面比较有优势[7]，但无法将列车模型细化。故将两种软件结合，运用SIMPACK软件建立车-路系统动力学仿真模型，结合青藏线格拉段的一段实际线路，通过其后处理模块得到不同线路参数下的动力学性能参数，将部分参数作为激励源导入运用ABAQUS建立的轨道结构有限元模型中，进而对动力特性指标进行研究分析。本研究与以往研究不同处在于：不仅从动力学角度考虑列车与线路之间的作用，而且还考虑了列车之间的相互作用以及轨道结构对列车运行的影响，从而得到旅客列车在该区段的临界速度以及提出旅客列车提速方案。

1 旅客列车及轨道结构模型

格拉段轨道结构的实际照片如图1所示。

图1 格拉段照片Fig.1 The picture of gelasection

客车动力学模型由轮对、构架、一系悬挂、二系悬挂和车体等组成。考虑到头车及尾车的影响，以3节客车模型为研究对象，列车模型由3个车体、12个构架、12个轮对共27个体组成。其中，车体及构架有6个自由度，即纵向、横向、垂向、侧滚、摇头、点头，前后8个轮对有3个自由度，即横向、垂向、摇头，整车共126个自由度，列车部分参数如表1所示[8]。

列车与轨道结构仿真模型如图2和图3所示。与车辆-轨道耦合分析一样，钢轨模拟采用Euler梁[9]。

轨道结构包括钢轨、轨枕、扣件、道床、路基等，钢轨与轨枕、轨枕与道床之间采用弹簧连接，运用ABAQUS建立轨道结构模型，其参数如表2所示。

表1 列车模型参数

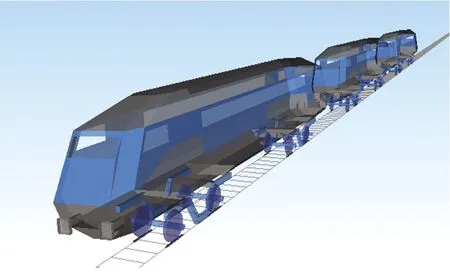
图2 列车仿真模型Fig.2 The simulation model of trains

图3 轨道结构模型Fig.3 The model of track structure

部件参数数值钢轨弹性模量/MPa2.06×106泊松比0.3垂向刚度/(N·m-1)7×107扣件横向刚度/(N·m-1)2.4×107垂向阻尼/(kN·s·m-1)75横向阻尼/(kN·s·m-1)60轨枕弹性模量/MPa3.75×104泊松比0.3道床弹性模量/MPa150泊松比0.27路基弹性模量/MPa60泊松比0.35

之前其他的研究模型采用单节列车，且将轨道结构作为刚性考虑，未研究轨道结构对列车运行的影响。本次研究在SIMPACK中建立列车仿真模型，按照格拉段实际线路参数添加线路模型及以轨道随机不平顺功率谱密度(power spectrum density,PSD)方式激励的青藏铁路轨道不平顺界限谱[10]，将仿真计算所得到的轮轨垂向力作为激励源导入运用ABAQUS建立的轨道结构模型中，因轮轨横向力相对于其垂向力较小，故可以忽略轮轨横向力的作用，考虑轨道结构及列车之间的相互作用对列车运行的影响，最终得到各运行评价指标。

钢轨振动加速度是铁路动力特性试验的主要指标[11]，得到列车以160 km/h在无不平顺的有砟轨道线路上运行时的钢轨垂向加速度如图4所示。

图4 钢轨垂向加速度结果Fig.4 The result of rail vertical acceleration

在80 kN的荷载作用下Mises应力分布云图如图5所示。可见除了轨头与车轮接触区应力最大之外，轨腰应力响应较大，达到25～50 MPa。可见图4与图5结果的变化趋势与变化幅度与文献[12-13]基本一致，进而验证本文车辆-轨道耦合模型的准确性。

图5 Mises应力分布云图Fig.5 The cloud picture of Mises stress distribution

选取青藏线格拉段某区段线路进行分析，选取的线路由两部分的直线段、进出缓和曲线段以及圆曲线段组成，其中第1段为右偏曲线，第2段为左偏曲线。该线路照片如图6所示。线路具体参数如表3所示。

图6 线路照片Fig.6 The picture of railway

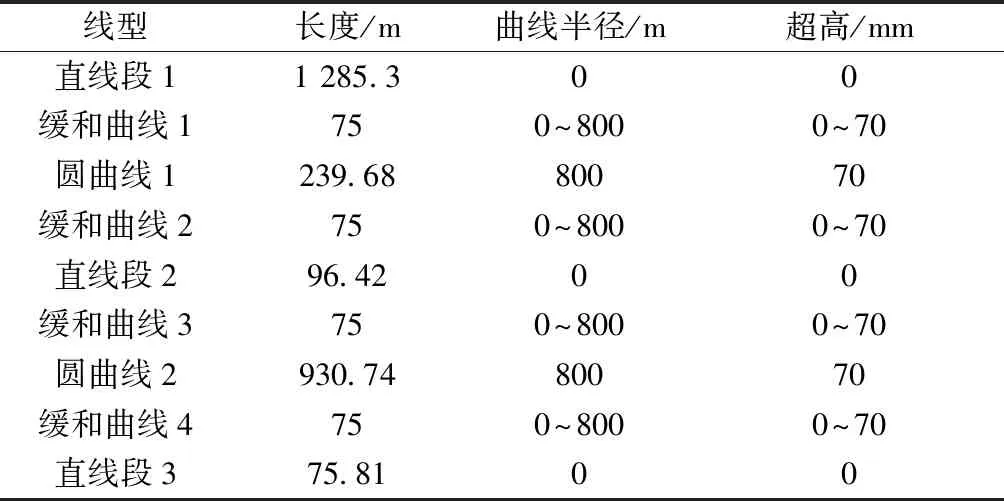
线型长度/m曲线半径/m超高/mm直线段11 285.300缓和曲线1750～8000～70圆曲线1239.6880070缓和曲线2750～8000～70直线段296.4200缓和曲线3750～8000～70圆曲线2930.7480070缓和曲线4750～8000～70直线段375.8100

2 列车动力学特性分析

2.1 车辆运行评价指标

车辆运行的安全性与稳定性是列车运营的基本条件，进行仿真分析后，能够得到多种动力学特性指标。此前多种仿真分析表明，采用脱轨系数以及轮重减载率作为列车运行安全性与稳定性的评价指标是可行的，其中，脱轨系数的表达式为

(1)

式(1)中：Q为轮对上的横向力，N；P为轮对上的垂向力，N；N为轨道对轮对的法向力，N；T为轨道对轮对的切向力，N；α为车轮的轮缘角，(°)。

根据《铁道车辆动力学性能评定和试验鉴定规范》[14]，脱轨系数不应大于0.8。轮重减载率表达式为

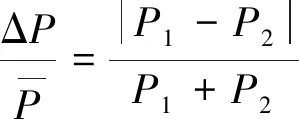
(2)

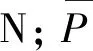
根据上述规范可知，轮重减载率不应大于0.6。

车辆垂向加速度是评定旅客乘坐舒适度的指标，对旅客列车垂向加速度a2规定的标准为

(3)

2.2 仿真结果分析

对于列车模型，以青藏线既有列车运行速度90 km/h进行仿真分析，得到前后6个转向架上的轮对所对应的动力特性指标随时间变化的关系，如图7及图8所示。

由仿真结果可知，列车通过直线段与圆曲线段时，头车和尾车的运行评价指标并无太大区别，而当列车通过缓和曲线路段时，尾车的脱轨系数比头车和中车的略大一些。其中，尾车前转向架的脱轨系数比头车和中车大了5.0%和2.5%，尾车后转向架的脱轨系数比头车和中车大了3.3%和1.2%；而对于同一辆车而言，头车后转向架上轮对的脱轨系数比前转向架上的大了10.9%。中车后转向架上轮对的脱轨系数比前转向架上的大了18.2%，尾车后转向架上轮对的脱轨系数比前转向架上的大了20.6%。

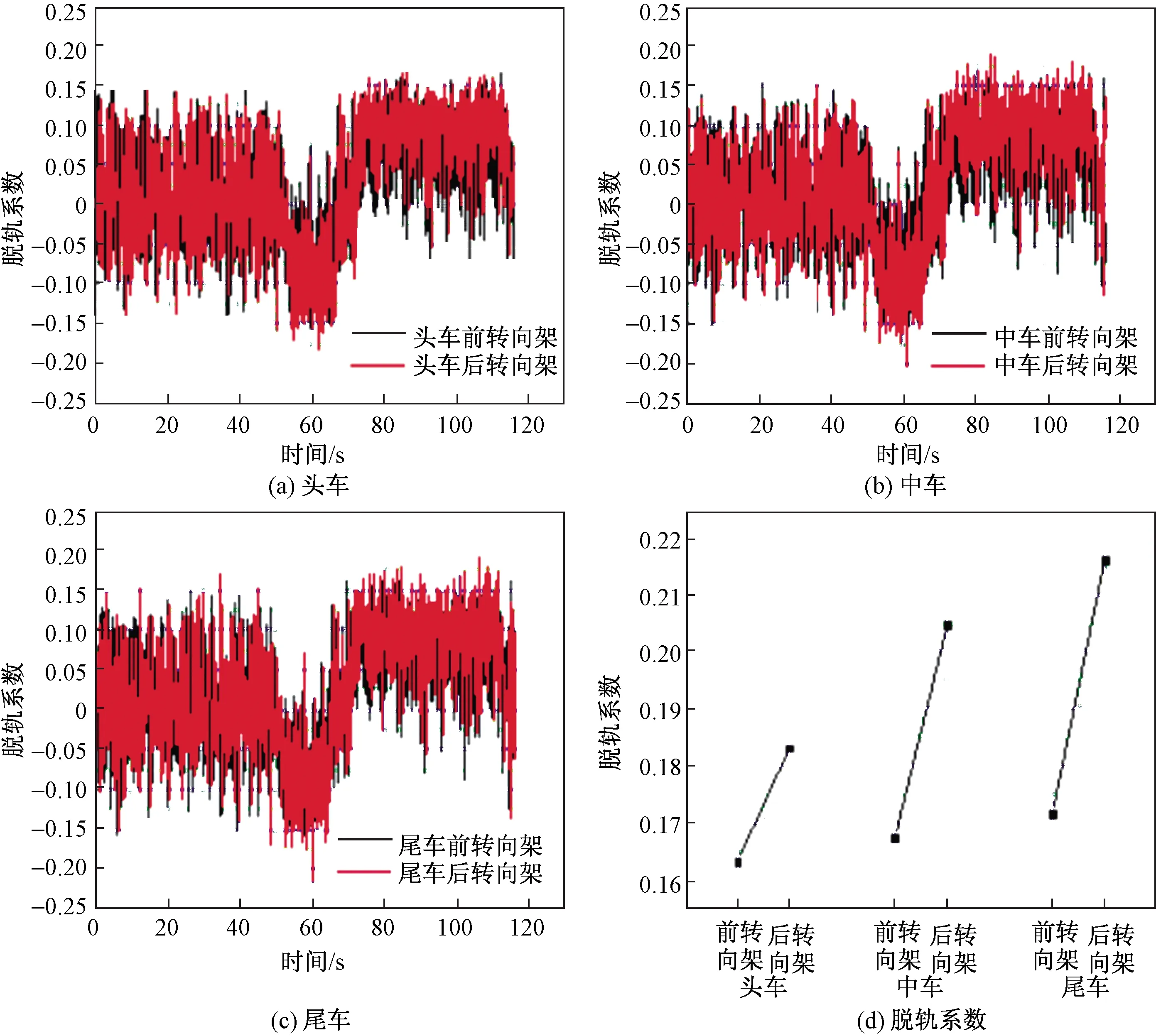
图7 速度90 km/h脱轨系数仿真值Fig.7 The derailment coefficient simulation value with the speed of 90 km/h

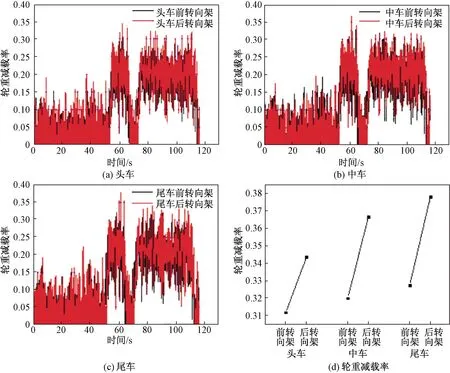
图8 轮重减载率仿真值Fig.8 The simulation value with the reduction rate of wheel road

且当列车通过曲线路段时，尾车的轮重减载率相对于头车和中车的轮重减载率呈增大趋势。其中，尾车前转向架上轮对的轮重减载率比头车和中车大了4.8%和0.8%，尾车后转向架上轮对的轮重减载率比头车和中车大了9.1%和3.0%；对于同一辆客车，头车后转向架上轮对的轮重减载率比前转向架上的大了9.2%，中车后转向架上轮对的轮重减载率比前转向架上的大了12.8%，尾车后转向架上轮对的轮重减载率比前转向架上的大了13.4%。

综上所述，当列车以运行速度90 km/h通过缓和曲线路段时，列车中尾车后转向架上轮对的动力特性指标均为最大，运用不同运行速度进行仿真分析，最终可得到：当列车以某一速度运行时，尾车后转向架上的轮对更容易发生脱轨，故以下研究分析均以列车组尾车后转向架上的轮对作为研究对象。

2.2.1 列车在原线路上的临界速度

经过仿真实验，得到原线路的临界速度仿真结果如图9所示。

轮对横移量小于0.1 mm就认为收敛[15]，由图9可得理论情况下列车通过线路区段的临界速度为109 km/h，且钢轨变形量最大值为0.405 mm，即现行列车以109 km/h的速度在格拉段上运行是安全稳定的。

2.2.2 曲线半径对列车运行的动力特性分析

当车辆运行速度提升至120 km/h时，经过仿真可以得到在此速度下的最小曲线半径，增大曲线半径后120 km/h时的各项动力特性指标结果如图10所示。

经仿真实验可知，随着线路曲线半径的增大，列车可安全平稳通过线路的最大速度也随之增大。当列车以120 km/h的速度在此线路上安全平稳运行时，曲线半径最少需要增至1 000 m，即可以通过

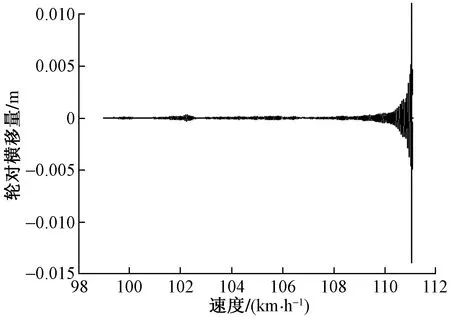
图9 临界速度仿真值Fig.9 Thesimulation results of the critical speed

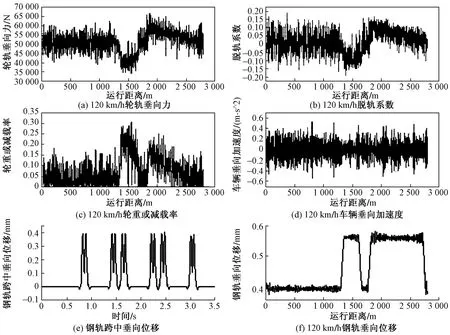
图10 曲线半径为1 000 m的仿真结果Fig.10 Simulation result with a curve radius of 1 000 m

增大曲线半径至1 000 m以上来实现列车的提速。

2.2.3 缓和曲线长度对列车运行的动力特性分析

将每段曲线的缓和曲线长度增至150 m，其余条件不变，进行仿真分析，得到的列车在缓和曲线上运行时的临界速度如图11所示。

由图11可知，当旅客列车通过线路中缓圆点以及圆缓点时，各项评价指标均会出现突变值。缓和曲线长度增为150 m时，列车在线路上能够运行的最大速度为114 km/h，即可以通过适当提高缓和曲线长度来提高列车运行的速度，但无法将运行速度提升至120 km/h，故缓和曲线长度增大到一定程度后没有必要继续增长。

2.2.4 超高对列车运行的动力特性分析

将列车运行速度提升至120 km/h，可以得到安全平稳通过线路的最大超高设置值，在此超高下的各项动力特性指标如图12所示。

图11 缓和曲线长度为150 m仿真结果Fig.11 Simulation result with a transition curve length of 150 m

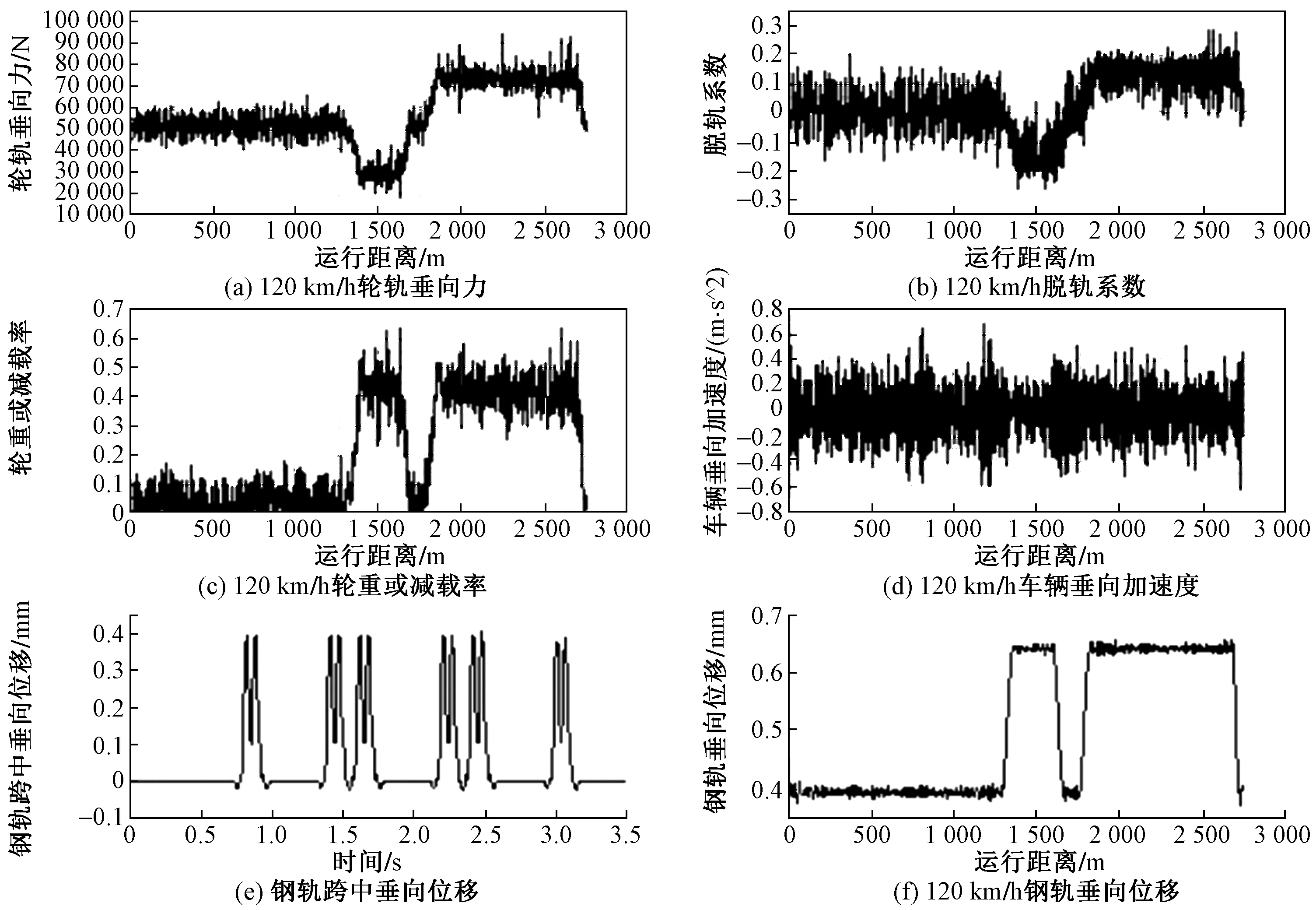
图12 外轨超高为100 mm仿真结果Fig.12 Simulation result with asuperelevation of 100 mm

由图12可知，随着外轨超高的增大，列车可安全平稳运行的最大速度也随之增大，可将外轨超高提升至100 mm，进而实现列车以120 km/h的速度在此线路上的安全平稳运行。

3 结论

(1)当列车通过曲线段时，其尾车后转向架上轮对的动力特性指标最大，即列车在曲线线路上运行时，尾车后转向架上的轮对更容易发生脱轨。

(2)理论情况下旅客列车通过该段线路时，能够安全平稳运行的最大速度为109 km/h。随着线路曲线半径、缓和曲线长度和外轨超高的增加，可以匹配到更高的车辆运行速度。当曲线半径提升至1 000 m及以上，外轨超高设置在100 mm及其以上时，列车均可以120 km/h的速度在此线路上安全平稳运行，增大缓和曲线长度对于列车提速方面的效果并不是十分明显，但增大缓和曲线长度可以改善旅客乘坐舒适度。

(3)从以上仿真结果中不难发现，动力特性指标较大值处均为直线与曲线的连接点处，即当列车通过这些连接点时，列车的轮对会撞击轨道，从而导致线路轨道不平顺，增大了轮轨间作用力，导致旅客舒适度较差。

综上所述，可以通过增大曲线半径和增加外轨超高来实现列车提速，通过增大缓和曲线长度可以改善旅客乘坐舒适度，进而提高青藏线格拉段铁路的运输效益。