对一道联考试题的探究

周腊生 陈晓明

摘 要：本文对一道解析几何模拟试题的解法进行探究，并揭示试题背景、探究问题本源.习题课教学要通过一个或几个题目的解决让学生领悟一类问题的知识背景，抓住一类问题的数学本质，特别是提炼解决一类问题的思想方法.

关键词：抛物线;焦点弦;准线

参加各级各类联考是高考复习过程中重要的一个环节，笔者所在学校每届高三都要参加在安徽享有盛誉的“皖南八校”联考.“皖南八校”2019届高三第三次联考理科数学第20题是一道解析几何试题，因为计算量较大的原因学生普遍害怕解析几何题，但本题计算量并不算大，学生得分率依然很低.本文对试题解法进行探究，并揭示试题背景、探究问题本源，从而更好地备考.

1 试题呈现

题目 在平面直角坐标系xOy中，已知抛物线C∶x2=2py（p>0），过抛物线焦點F且与y轴垂直的直线与抛物线相交于A，B两点，且△OAB的周长为2+5.

（1）求抛物线C的方程;

（2）若直线l过焦点F且与抛物线C相交于M，N两点，过点M，N分别作抛物线C的切线l1，l2，切线l1与l2相交于点P，求|PF|2-|MF|·|NF|的值.

2 解法探究

2.1 第（1）问解析

解析 由题意知焦点F的坐标为（0，p 2）.

将y=p 2代入抛物线C的方程可求得点A，B的坐标分别为（-p，p 2），（p，p 2）.

故|AB|=2p，|OA|=|OB|=p2+（p 2）2=5 2p.

所以△OAB的周长为2p+5p.

所以2p+5p=2+5，解得p=1.

所以抛物线C的方程为x2=2y.

2.2 第（2）问解析

解法1 如图1所示，由（1）知抛物线C的方程可化为y=1 2x2，求导可得y′=x.

设点M，N的坐标分别为（x1，y1），（x2，y2），设直线l的方程为y=kx+1 2.（直线l的斜率显然存在）

联立方程y=kx+1 2，y=1 2x2，

消去y整理，得x2-2kx-1=0.

因为根的判别式△=4k2+4>0，

所以由韦达定理，得x1+x2=2k，x1x2=-1.

所以y1+y2=k（x1+x2）+1=2k2+1，

y1y2=1 4x21x22=1 4.

直线l1的方程为y-1 2x21=x1（x-x1）.

整理，得y=x1x-1 2x21.

同理，直线l2的方程为y=x2x-1 2x22.

联立方程组y=x1x-1 2x21，y=x2x-1 2x22，解得x=x1+x2 2，y=x1x2 2.

所以点P的坐标为（k，-1 2）.

所以由抛物线的几何性质，知|MF|=y1+1 2，|NF|=y2+1 2.

所以|MF|·|NF|=（y1+1 2）（y2+1 2）=y1y2+1 2（y1+y2）+1 4=1 4+1 2（2k2+1）+1 4=k2+1.

又由两点间距离公式，得

|PF|=（k-0）2+（-1 2-1 2）2=k2+1.

所以|PF|2-|MF|·|NF|=k2+1-（k2+1）=0.

评注 （1）本解法属通性通法，朴实无华.设出直线方程、联立抛物线方程，得到韦达定理，这是在解析几何中比较常见的解法.将所求线段之积|MF|·|NF|用抛物线的焦半径表示，然后利用韦达定理得到的结论及直线方程代入，得出只含参数k的式子.另一方面，利用导数求出两切线方程，联立解得点P坐标，这也是很常规的解法，然后由两点间距离公式求出|PF|，同样只含参数k，从而进一步算出美妙的答案（参数k设而不求）.纵观整个过程，计算量并不是很大，为什么学生不能解出正确答案呢？问题出在上述过程的哪个环节？有的是学生想不到;有的是想到了却不敢算;有的是计算时细节出了问题;……总之，基本功不扎实，知识掌握不熟练，计算能力欠缺.

（2）将直线方程与抛物线方程联立时也可以消去x，得到关于y的一元二次方程，然后利用韦达定理解决问题.

（3）计算|MF|·|NF|的值可不用抛物线焦半径公式，利用两点间距离公式、韦达定理解决问题.

|MF|·|NF|=x21+（x21 2-1 2）2·x22+（x22 2-1 2）2

=x21+1 2·x22+1 2

=（x1x2）2+x21+x22+1 4

=1+（x1+x2）2-2x1x2+1 4

=k2+1.

解法2 如图1所示，由解法1知，直线PM，PN斜率之积kPMkPN=x1x2=-1，故PM⊥PN.

又因为点P（k，-1 2），所以直线PF，MN斜率之积kPFkMN=-1 2-1 2 k-0·k=-1.

所以PF⊥MN.

在Rt△PMN中，由射影定理得|PF|2=|MF|·|NF|.

所以|PF|2-|MF|·|NF|=0.

评注 解法1是代数法，解法2是几何法，两种方法交相辉映、数形结合、相得益彰！相比代数法，几何法更为简洁、神奇！原来本试题还隐藏着这样的几何背景，令人感慨.

3 提出问题

不难发现，这里MN为抛物线x2=2y的焦点弦，过其两端点M，N所作切线交点P（k，-1 2）正好落在抛物线的准线y=-1 2上，且PF⊥MN，PM⊥PN，由xP=x1+x2 2可知点P与MN中点横坐标相同，这是巧合吗？结论能推向一般吗？逆命题成立吗？

4 追根溯源

定理1 若直線l过焦点F且与抛物线C∶x2=2py（p>0）相交于M，N两点，过点M，N分别作抛物线C的切线l1，l2，切线l1与l2相交于点P，线段MN中点为Q.则有下列结论成立：

（1）xP=xQ;

（2）点P在抛物线的准线y=-p 2上;

（3）PF⊥MN;

（4）PM⊥PN;

（5）|PF|2-|MF|·|NF|=0.

证明 如图2所示，抛物线C的方程可化为y=x2 2p，求导可得y′=x p.

设点M，N的坐标分别为（x1，y1），（x2，y2），设直线l的方程为y=kx+p 2.（直线l的斜率显然存在）

联立方程y=kx+p 2，y=x2 2p，

消去y整理，得x2-2pkx-p2=0.

因为根的判别式△=4p2k2+4p2>0，

所以由韦达定理，得x1+x2=2pk，x1x2=-p2.

所以y1+y2=k（x1+x2）+p=2pk2+p，

y1y2=x21x22 4p2=p2 4.

直线l1的方程为y-x21 2p=x1 p（x-x1）.

整理，得y=x1x p-x21 2p.

同理，直线l2的方程为y=x2x p-x22 2p.

联立方程y=x1x p-x21 2p，y=x2x p-x22 2p，解得x=x1+x2 2，y=x1x2 2p.

所以点P的坐标为（pk，-p 2）.

由xP=x1+x2 2，且Q为线段MN中点知xP=xQ.

因为点P（pk，-p 2），所以点P在抛物线的准线y=-p 2上.

所以直线PM，PN斜率之积kPMkPN=x1x2 p2=-p2 p2=-1，即PM⊥PN.

又因为点P（pk，-p 2），所以直线PF，MN斜率之积kPFkMN=-p 2-p 2 pk-0·k=-1，所以PF⊥MN.

在Rt△PMN中，由射影定理，得|PF|2=|MF|·|NF|，故|PF|2-|MF|·|NF|=0.

评注 （1）将问题由特殊推向一般，结论仍然成立.

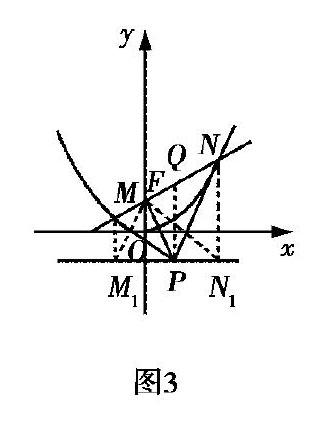
（2）这里证明垂直关系方法不唯一，如图3所示，分别过点M，N向抛物线的准线y=-p 2作垂线，垂足分别为点M1，N1，连结FM1，FN1.

先证明PM⊥PN.易知|PQ|=1 2（|MM1|+|NN1|）=1 2（|MF|+|NF|）=1 2|MN|.

所以P，M，N三点在以MN为直径的圆上.

所以∠MPN=π 2，即PM⊥PN.

再证明PF⊥MN.因为F（0，p 2），M1（x1，-p 2），所以FM1=（x1，-p）.同理FN1=（x2，-p）.

所以FM1·FN1=x1x2+p2=-p2+p2=0（由命题证明知x1x2=-p2），即FM1⊥FN1.

又因为点P为M1N1的中点，

所以|PF|=1 2|M1N1|=|PM1|.

故∠PFM1= ∠PM1F.

又|MM1|=|MF|，所以∠MFM1=∠MM1F.

故∠PFM=∠PFM1+∠MFM1=∠PM1F+∠MM1F=π 2，即PF⊥MN.

（3）抛物线的焦点弦性质还有很多，读者可参阅笔者文章《抛物线的焦点弦性质及应用》[1].

（4）不难证明，上述定理的逆命题也成立.

定理2 已知点P为抛物线C：x2=2py（p>0）的准线上任意一点，过点P分别作抛物线C的切线l1，l2，切点分别为点M，N，线段MN中点为Q，则有下列结论成立：

（1）xP=xQ;

（2）切点弦MN过抛物线的焦点;

（3）PF⊥MN;

（4）PM⊥PN;

（5）|PF|2-|MF|·|NF|=0.

题源揭秘 其实，本联考试题的背景是“阿基米德三角形”：抛物线的弦与过弦的端点的两条切线所围的三角形称为阿基米德三角形.阿基米德三角形的得名，是因为阿基米德本人最早利用逼近的思想证明了结论：抛物线的弦与抛物线所围成的封闭图形的面积，等于抛物线的弦与过弦的端点的两条切线所围成的三角形面积的三分之二.上述定理1、定理2都是阿基米德三角形的性质，即“弦为焦点弦”与“弦端点处切线交点在准线上”存在对应关系.

5 试题链接

题目 （2019年高考全国Ⅲ=3＼*ROMAN卷理科第21（1）题）已知抛物线C：y=x2 2，D为直线y=-1 2上的动点，过点D作C的两条切线，切点分别为A，B，证明：直线AB过定点.

提示 由上述逆命题知，因为点D是直线y=-1 2 （抛物线y=x2 2的准线）上的点，故直线过抛物线的焦点（0，1 2）.

6 结束语

我们的习题课教学要通过一个或几个题目的解决让学生领悟一类问题的知识背景，抓住一类问题的数学本质，特别是提炼解决一类问题的思想方法，培养学生研究问题的能力，构建相关数学知识的内部网络，从而让学生对该类问题的再次考查而跃跃欲试，不再害怕考试，不再害怕做题！正如美国著名数学教育家波利亚所说：“一个专心的认真备课的老师能够拿出一个有意义但又不太复杂的题目，去帮助学生挖掘问题的各个方面，使得通过这道题，就像通过一道门户，把学生引入一个完整的理论领域.”

参考文献：

[1]陈晓明.抛物线的焦点弦性质及应用[J].理科考试研究，2018（15）：17-20.

[2]于世章.挖掘课本习题价值上好复习课[J].数学通报，2014，53（12）：36-38.

（收稿日期：2020-11-03）