圆形薄膜预应力测量

谭昭 ，吴时彬 ，杨伟 ，翟嘉

(1.中国科学院光电技术研究所，成都 610209； 2.中国科学院大学，北京 100049)

高分子薄膜厚度薄、质量轻、种类多，在微电子领域可作为敏感元件及半导体器件等各种器件，是实现器件和系统微型化的有效的技术手段之一[1]。薄膜内应力的分布能够直接影响微电子薄膜器件的寿命及性能。在光学方向，薄膜可作为反射膜、干涉滤波片等[2]。美国于2010 年开展了衍射薄膜成像项目(“MOIRE”计划)。衍射薄膜是将以衍射光学为工作原理的菲涅尔透镜制作在薄膜基底上的光学元件，具有质量轻、厚度薄、公差容限大等优点[3]。

无论对于哪种类型的薄膜来说，结构刚度都是一个十分重要的参数。而薄膜是柔性体，它的结构刚度主要取决于边缘几何外形和预应力水平[4]。所以在应用时预先施加合理大小的预应力对薄膜后续使用十分重要。而且预应力不仅与薄膜的成型和使用寿命息息相关，其引起的形变也会影响薄膜光学性能与力学性能[5–6]，所以测量预应力是薄膜的一个重要课题。如今薄膜的应力检测技术主要分为以下几种方法：

(1) 1906 年 Stoney 提出经典的 Stoney 公式。Stoney 公式主要描述了薄膜应力变化与引起的基底曲率变化之间的关系。由此衍生了Stoney 公式法利用测量基底曲率变化来测量薄膜残余应力的方法。基底曲率法、激光干涉法、光栅反射法等均是Stoney 公式法的一种[7]。但这类方法比较适合测量薄膜成型中或者成型后的应力，对后期薄膜无基底应用时的预应力无法进行测量。

(2) X 射线衍射法是通过测量应力引起的点阵间距变化所导致的弹性应变转换为应力的测量方法[5]。微观拉曼光谱法是利用激光拉曼光谱技术标定出纤维所受应变与拉曼光谱频率位移之间的关系来测量薄膜应力[8]。这类方法是通过测量微观变化量再转化成应力大小，使用的仪器大多比较昂贵，并且对薄膜的材料特性有一定的要求。

(3)应力应变片是通过贴在被测物上，通过测量被测物应变变化来计算应力大小，在应力测量方面有广泛的应用。但是应力应变片是接触式的测量，对于柔性体的薄膜来说，使用时十分容易使薄膜产生褶皱，影响测量结果，同时会影响到薄膜后续使用。

(4)拉伸法是在薄膜边缘节点处安装载荷传感器，拉伸薄膜直接测出应力的大小。这样直接测出的应力数据可靠性高，但是测量的是薄膜的变化量，而且有时可能对薄膜造成破环。

(5) 2001 年日本尼康株式会社的铃木用掩模版膜内应力测试装置及方法向美国申请专利[9]。介绍了薄膜对冲击响应产生的振动频率反馈推算出薄膜预应力的测量方法。日本鹿岛建设株式会社运用了薄膜对均匀载荷产生的位移变化推测应力的位移法[10]。这两种方法无需对薄膜进行破环就可以测得薄膜应力，缺点是对薄膜前期的建模、标定及边界的设定条件比较难。

而对于装配好的薄膜来说，需要一种不会影响到薄膜后续使用的无损测量方法。而且使用中的薄膜无法主观直接改变预应力的大小，需要测量应力绝对值的方法。对于这两点需求，应力应变片、拉伸法、微观拉曼光谱法等方法都不适用。位移法和频率测试法是一种无损测量薄膜应力绝对值的方法，其中位移法控制的变量相比于频率测试法更少，实验更加简单。

对于不同材料和形状的薄膜，位移法都需要前期的建模与标定实验。日本鹿岛建设株式会与同济大学等均对建筑上矩形薄膜进行了分析与实验[11–12]。重庆大学的吴建梁等对圆形薄膜进行了理论分析但是缺少实验验证部分[12–13]。

笔者主要是利用位移法测量圆形薄膜预应力。考虑理论与实验的结合。首先设计实验利用密封腔改变对薄膜作用的均匀载荷，测量得出均匀载荷下薄膜的中心挠度。然后用有限元软件ABAQUS 建立的模型求出预应力的有限元解，再利用理论方程建立模型求出中心位移，与实验及有限元解进行对比，判断位移法能否应用于圆形聚酰亚胺薄膜预应力的测量。

1 理论计算圆形薄膜预应力

Von Karman 于1910 年提出薄板大挠度理论的微分方程——Von Karman’s 方程。随着工业的发展，理论模型在不断完善[13–15]。图1 为薄膜受力简图，其中r是薄膜径向坐标，取值0～R(半径)；q是施加的均匀载荷。

图1 薄膜受力简图

根据Von Karman’s 方程，推导出施加均匀预张力圆薄膜的基本方程与圆薄膜变形协调方程见式(1)、式 (2)[15]。

式中：Nr是薄膜单位长度径向力；w是挠度；E是弹性模量；h是薄膜厚度。

边界条件：r=R时，w=0，u=0，u为薄膜径向位移。r=0 时，Nr有限。引入无量纲变量：

其中N0为预应力；υ为泊松系数。

则方程(1)与方程(2)可以改写并合并为：

薄膜边界条件为：当x=1 时，2(xSr)′– (1+υ)(xSr)=S0(1–υ)；当x= 0 时，Sr有限。

方程(9)在边界条件下的解为

其中

a是预紧力与泊松比以及测量点位置决定的参数，可通过计算求解。

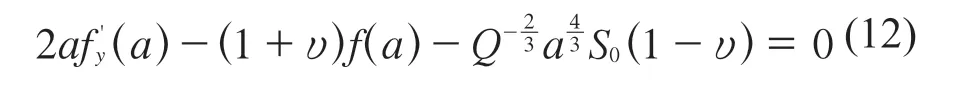
可由式(10)求得a后，再将a代入式(12)求得S0，可得预应力大小。反之也可求得相应预应力下的薄膜中心位移。

2 有限元分析

在数学中，有限元法是一种为求解偏微分方程边值问题近似解的数值技术。有限元不仅计算精度高，而且能适应各种复杂形状，因而成为行之有效的工程分析手段。而ABAQUS 是一套功能强大的工程模拟有限元软件，可以解决从相对简单的线性分析到许多复杂的非线性问题。

考虑到薄膜结构的特殊性采用ABAQUS 中的三维壳单元建立模型。赋予模型相对应的参数见表1。通过静力通用分析步对薄膜边缘施加均匀径向边载荷，模拟薄膜预应力。运用动力隐式的分析步对薄膜施加压强，使用三角形的自由网格对薄膜进行网格划分。有限元模型的网格划分见图2。

表1 薄膜材料参数

图2 有限元模型网格划分示意图

利用边载荷施加1 MPa 预应力，薄膜面内应力分布见图3a。确认薄膜施加边缘载荷后薄膜面内应力分布均匀，可以用此方法模拟预应力的施加。在面上施加10 Pa 均匀压强，通过后处理程序查看薄膜面内位移，见图3b，薄膜中心位移为0.316 5 mm。

图3 薄膜面内应力分布及位移分布

3 实验测量预应力

实验使用的薄膜为聚酰亚胺薄膜，与有限元分析对象一致，薄膜参数见表1。为了对薄膜施加均匀载荷，将薄膜的一面密封形成一个密封腔，利用气压缸改变密封腔内压强，产生的压强q为均匀载荷，用压差表测量压强q。利用测距仪测量薄膜中心挠度产生位移变化y0，记录薄膜中心点的位移数据。图4 为实验原理示意图。

图4 实验原理示意图

将装配好的薄膜一面与一个口径和薄膜框口径相同的钢板相连接。并用密封胶将空隙补好形成一个密封腔。采用德国德图testo510 压差表测量气压值，精度为1 Pa。利用气压缸向密封腔内充入一定的空气，形成与外界的压强差。经过一段时间确保压强无变化来证明所形成的空间的密封性。连接好仪器，压差表归零，利用气压缸改变密封腔内压强。每增减5 Pa 压强记录测距仪的数据及对应的压强。测距仪采用基恩士LK–H022K 型，精度为0.001 mm。图5 为实验装置图。

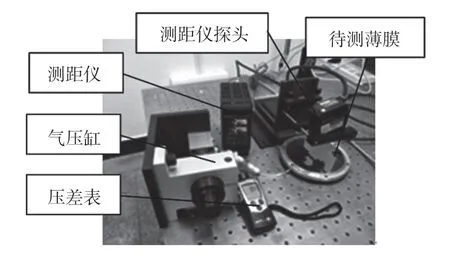
图5 实验装置图

表2 为实验得出的结果，其中数据1 与2 是第一组预应力下的两组重复实验的数据；数据3 与数据4 是第二组预应力下的数据。

表2 实验数据

4 结果与分析

得到数据后，进行以下几步数据的处理计算。

(1)任选一个压强下的薄膜中心位移数据作为基准，运用有限元求出对应的预应力。

例如，数据2 中，在40 Pa 压强下薄膜中心位移为0.163 mm。利用有限元求出薄膜预应力为7.933 MPa。图6 是有限元应力分布及位移分布图。

(2)改变压强，用有限元计算在该预应力下其它压强对应的薄膜中心位移。

图6 有限元应力分布及位移分布

(3)计算在该预应力下，薄膜在各个压强下的中心位移的解析解。

例如，将预应力N0=7.933 MPa，压强q=40 Pa及薄膜参数带入公式(7)、公式(8)可求出Q=194 100，S0= –1 237 600。

再将参数带入公式(12)为：

求得a=2.0×10–8，以及待求的为薄膜中心位移x=0。将参数代入式(10)求得薄膜中心位移y为0.159 mm。

(4)另选择一组或者几组数据重复(1)～(3)步骤，确认数据的可靠性。

例如，20 Pa 压强下薄膜中心位移为0.083 mm，有限元求出薄膜预应力为7.794 MPa。再求出在对应预应力不同压强下的薄膜中心位移的解析解及有限元解。

(5)将上述计算数据与实验数据进行对比。表3 为第一组预应力下的数据计算结果，其中A 为7.933 MPa 预应力下的薄膜中心位移的有限元解，B 为7.933 MPa 下的薄膜中心位移的解析解，C 为7.794 MPa 下的薄膜中心位移的有限元解，D 为7.794 MPa 下的薄膜中心位移的解析解。图7 为实验与计算结果的对比散点图。

第二组预应力下运用相同的方法进行计算。由数据4 得出在35 Pa 压强下薄膜中心挠度为0.209 mm，有限元计算预应力为5.468 MPa；45 Pa 压强下薄膜中心挠度为0.258 mm，有限元计算预应力大小为5.694 MPa。再进行不同压强下的薄膜中心挠度的计算，图8 为结果对比图，其中E 为5.468 MPa 下的薄膜中心位移的有限元解，F 为5.468 MPa 下的薄膜中心位移的解析解，G 为5.694 MPa 下的薄膜中心位移的有限元解，H 为5.694 MPa 下的薄膜中心位移的解析解。

表3 数据计算结果

图7 第一组预应力下实验与计算结果的对比散点图

图8 第二组预应力下实验与计算结果的对比散点图

通过上述理论与实验的验证，在同样大小的均匀载荷下，理论模型与有限元模型计算的中心位移误差均在6%以内。在取不同的压强组作为计算预应力的参考值时，预应力的差值也在2%以内。

5 结论

(1) Von Karman’s 方程可以用于大径厚比的高分子薄膜材料，可以通过这个方程计算均匀压强下的薄膜中心挠度变化，利用方程推算薄膜预应力的方法能够应用于实际的薄膜上。

(2)从原理上实现了薄膜预应力的无损测量，无需和薄膜有相应的接触，任选几组压强可求出薄膜预应力，不会导致载荷过大对薄膜产生破环。

(3)位移法测量的是薄膜应力的绝对值，而不是拉伸法或者应力应变片等方法测量的变化量。在实际应用时，对于已经装配好的薄膜镜来说，无法改变薄膜预应力，但是需要判断装配好的薄膜的预应力是否与预期施加的预应力符合，可以通过均匀载荷下测量中心挠度的方法来验证薄膜的预应力是否与预期相符合，也可以通过这种方法测量薄膜长时间使用后预应力的变化来判断薄膜是否失效。