基于MATLAB的单绳抓斗开闭机构运动学和动力学分析
禹 昭
(宁夏大学新华学院,宁夏 银川 750021)
0 引言
机械式抓斗按其开闭斗的操作方式可分为单绳抓斗和双绳抓斗两种类型。单绳抓斗操作方便,抓斗悬挂驱动时所需设备投入低,广泛应用在钻孔灌注桩等桩基础施工中。单绳抓斗的开闭机构是其工作时的主要运动和传力部件,在抓斗开闭机构的设计过程中,通常需要进行计算以确定开闭机构的几何尺寸,如拉杆长度、铰点相对位置等;另外为了满足抓斗的使用性能要求,必须进行必要的强度、刚度、可靠性及稳定性等方面的设计计算。这些设计计算,都需要对开闭机构进行运动学和动力学分析。
本文基于MATLAB软件,结合单绳抓斗开闭机构的实际结构,建立开闭机构的运动模型,并进行运动学和动力学分析,以便于直观地了解开闭机构各构件在运动过程中的运动和受力变化情况,为单绳抓斗开闭机构的设计计算提供参考,并为机构进一步的优化设计做准备。
1 单绳抓斗开闭机构运动模型的建立
1.1 抓斗开闭机构
单绳抓斗通常采用内拉杆式结构,抓斗内部装有增力动滑轮组,以提高闭斗力;抓斗顶部的吊斗装置与脱挂器配合动作可实现抓斗开闭的单绳操作。单绳抓斗开闭斗状态如图1所示,增力动滑轮组安装在动滑轮架上,抓斗闭合时,操纵钢丝绳通过增力动滑轮组带动动滑轮架上移,从而拉动拉杆移动,带动斗壳绕固定铰点转动,实现闭斗动作。
1.2 机构运动模型
开闭斗机构以抓斗轴线为中心,左右为对称结构,因此可以取其一半结构进行研究。以抓斗壳与抓斗筒体联接的固定铰点为坐标原点,平行于抓斗轴线为x轴,垂直于抓斗轴线为y轴,建立坐标系。抓斗开闭机构运动模型如图2所示,抓斗壳1等效为曲柄,拉杆2等效为连杆,动滑轮架3等效为滑块,抓斗筒体4等效为机架;抓斗壳1与抓斗筒体4联接的固定铰点等效为铰点A,抓斗壳1和拉杆2的联接铰点等效为铰点B,拉杆2和动滑轮架3的联接铰点等效为铰点C。
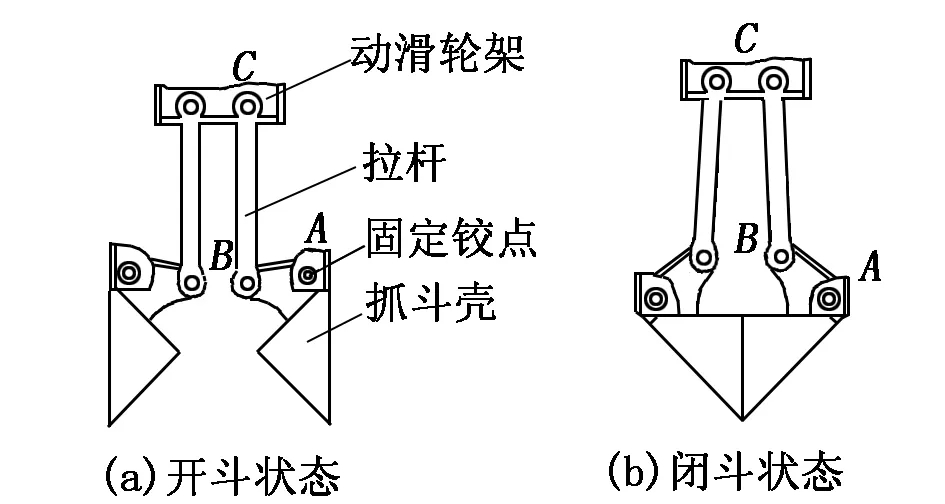
图1 单绳抓斗开闭斗状态示意图
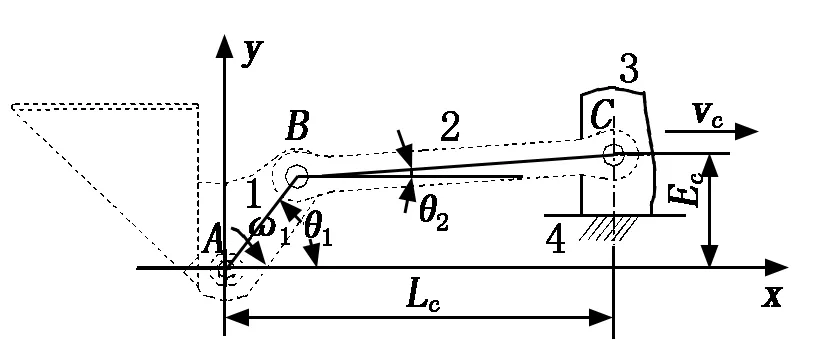
1-抓斗壳;2-拉杆;3-动滑轮架;4-抓斗筒体
2 运动学分析
2.1 位移、速度、加速度分析
根据图2所示,可写出抓斗开闭机构各构件所构成的封闭矢量方程:
l1+l2=Lc+Ec.
(1)
式(1)对时间t求一次导数,并用矩阵形式来表示,得速度关系表达式:
(2)
其中:ω1、ω2分别为抓斗壳1和拉杆2的角速度。
将式(2)对时间t求导数,并用矩阵形式来表示,可得加速度关系表达式:

(3)
其中:α1、α2分别为抓斗壳1和拉杆2的角加速度。
2.2 运动学求解
抓斗在闭斗过程中,钢丝绳通过动滑轮组带动动滑轮架3以速度vc移动,从而带动联接在动滑轮架上的拉杆2移动,在拉杆2的拉动下抓斗壳1绕铰点A转动;抓斗在开斗过程中,抓斗壳1以角速度ω1转动。以某型号单绳抓斗为例,初始条件如下:抓斗壳1两个铰点的距离l1=365 mm,拉杆2长度l2=1 000 m,EC=360 mm,vc=150 mm/s;开闭斗过程中抓斗壳1转动的角度变化范围θ1=53°~98°。
利用MATLAB编写程序进行求解,可以得到抓斗开闭机构的位移、速度、加速度曲线,如图3所示。



图3 抓斗开闭机构运动学分析结果
3 动力学分析
3.1 惯性力和惯性力矩
借助抓斗Pro/E三维模型可以得出开闭机构各构件的质心位置,忽略各处的摩擦力,并进行受力分析,如图4所示。
由前边的位移、速度、加速度分析结果,进一步计算,可得抓斗壳1质心的加速度在x轴和y轴'的分量表达式aS1x、aS1y:
(4)
其中:lAS1为抓斗壳1的质心S1与A点的距离;θS1为抓斗壳1质心与x轴的夹角,本文的研究算例中θS1=θ1+85°。
拉杆2质心的加速度在x轴和y轴的分量aS2x、aS2y的表达式为:
(5)
其中:lBS2为拉杆2质心S2与B点的距离。
动滑轮架3质心的加速度在x轴和y轴的分量aS3x、aS3y的表达式为:
(6)
抓斗壳1质量为m1,拉杆2质量为m2,动滑轮架3质量为m3,抓斗壳1的转动惯量为JS1,拉杆2的转动惯量为JS2;用F1x、F1y表示抓斗壳1质心的惯性力在x轴和y轴的分量,F2x、F2y表示拉杆2质心的惯性力在x轴和y轴的分量,F3x、F3y表示动滑轮架3质心的惯性力在x轴和y轴的分量,M1、M2表示抓斗壳1质心和拉杆2质心的惯性力矩。由构件质心的加速度和构件的角加速度可以确定其惯性力和惯性力矩表达式:
(7)
3.2 平衡方程的建立
基于图4所示,由抓斗壳1、拉杆2、动滑轮架3的受力分析及公式(7),根据∑M=0、∑Fx=0、∑Fy=0写出平衡方程,并解出运动副反力和力矩等未知量。为便于MATLAB编程求解,将线性方程组写成矩阵形式,如式(8)所示:
CFR=D.
(8)
其中:C为系数矩阵;FR为未知力列阵;D为已知力列阵。系数矩阵的表达式为:
(9)
其中:xS1、yS1为抓斗壳1的质心S1的坐标;xS2、yS2为拉杆2质心S2的坐标;xA、yA、xB、yB、xC、yC分别为铰点A、B、C点的坐标。未知力矩阵和已知力矩阵的表达式为:
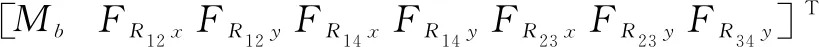
(10)
(11)
其中:Mb为抓斗壳1上的力矩;FR12x、FR12y、FR14x、FR14y、FR23x、FR23y、FR34y分别为各铰点支反力在x轴和y轴的分量。

图4 开闭机构受力分析
3.3 动力学求解
本文的计算实例中,由抓斗的Pro/E三维模型可以得出各构件的质心、质量及转动惯量:lAS1=350 mm,lBS2=500 mm;m1=510 kg,m2=100 kg,m3=250 kg,JS1=181.3 kgm2,JS2=35.5 kgm2。闭斗时,动滑轮架3上作用在钢丝绳滑轮组的最大拉力等于抓斗的总重量乘以滑轮组的倍率,本文取其一半结构进行研究,取Fr=180 000 N 。
利用MATLAB编写程序进行求解,可以得到抓斗开闭机构各铰点支反力和力矩,如图5所示。

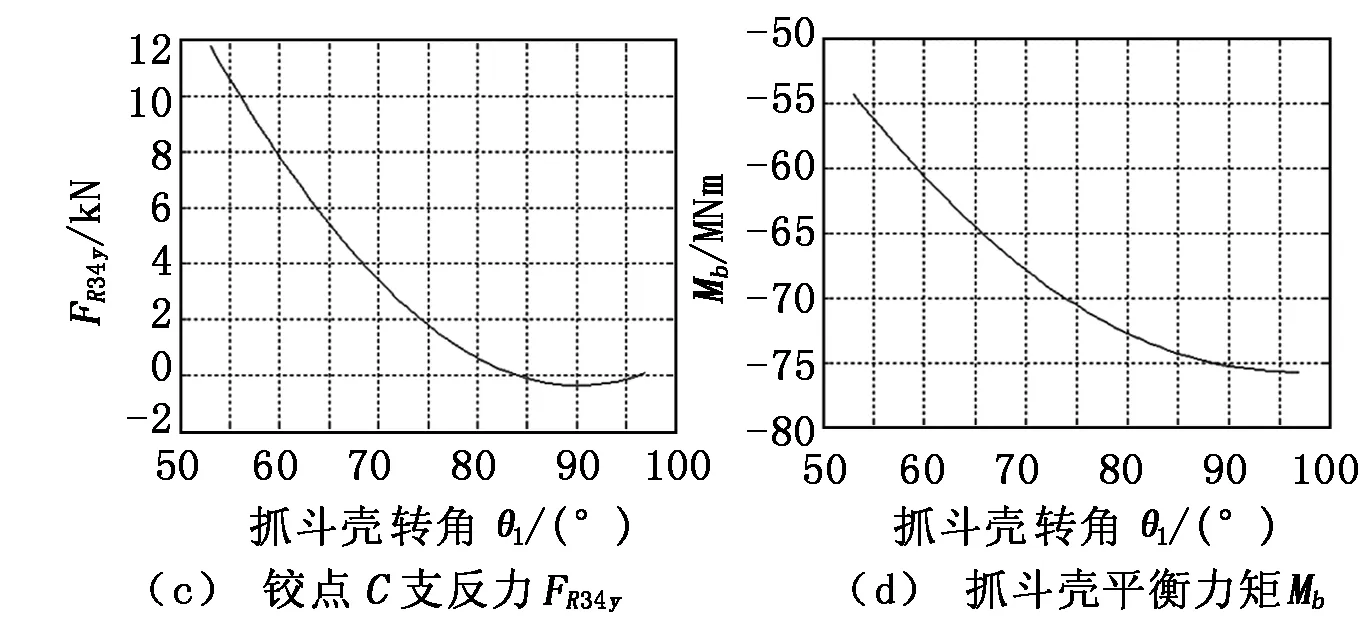
图5 抓斗开闭机构动力学分析结果
4 结果分析
(1) 抓斗开闭过程中,拉杆2转动的角度非常小,只有大约4°;动滑轮架3移动的范围为950 mm~1 220 mm;动滑轮架3虽然做变加速直线运动,但加速度的数值较小。
(2) 抓斗壳1与抓斗筒体4的联接铰点A、抓斗壳1和拉杆2的联接铰点B在y方向的支反力均很小,x方向的支反力较大,这与实际情况相符。
(3) 抓斗闭斗过程中,抓斗壳1的转角从98°逐渐减小到53°,抓斗壳1上的最大挖掘力矩从75 MNm逐渐减小到55 MNm。
5 结语
利用MATLAB软件结合抓斗实际结构得到了抓斗开闭机构仿真模型,通过求解可以得到机构运动过程中运动学和动力学的解析解,并且可以直观地通过图形展示出来,能为抓斗开闭机构的设计提供参考。该方法可以代替传统的图解法或实验方法,为抓斗的设计优化提供一种更加简便有效的设计方法。

