轨道结构参数变化对隧道振动的影响
熊永亮,许永富,王 博
(1.同济大学铁道与城市轨道交通研究院,上海 200000) (2.宁波市轨道交通集团有限公司,浙江 宁波 315000) (3.浙江天铁实业股份有限公司,浙江 台州 331000)
近年来,随着我国城市发展进程的加快,轨道交通愈加成为城市交通制式的不二选择。城市轨道交通的主要形式为地铁,其运营时对周围环境产生的振动影响引起了人们的广泛关注[1]。马龙祥等[2]通过建立薄片有限元-无限元耦合模型分析了地铁运营引发的环境振动响应,发现列车运营引发的纵向振动响应具有同横向、垂向响应相当的量值;刘鹏辉等[3]通过对北京某地铁线路内普通道床、III型轨道减振器、弹性短轨枕、梯形轨枕、钢弹簧浮置板等轨道结构的现场测试,发现梯形轨枕、弹性短轨枕、轨道减振器对50 Hz以上的振动减振效果明显,钢弹簧浮置板道床对12.5 Hz 以上的振动减振效果明显,对控制列车运行产生的二次噪声更有效。大量学者[4-7]通过实测、建模等方法研究了多种轨道结构的振动特性,为我国轨道交通的发展提供了大量宝贵的参考资料及建议,但针对不同轨道结构在实际运用过程中参数变化导致的轨道结构及隧道振动变化情况的研究较少。我国城市轨道交通轨道结构的多样化,使得每次改造的成本巨大,因此有必要对不同轨道结构参数变化对轨道结构及隧道振动的影响进行研究。本文选择整体道床、隔离式减振垫浮置板轨道、钢弹簧浮置板轨道这3种常用的轨道结构,采取有限元仿真方法模拟多种工况,对参数变化产生的影响进行研究分析并作对比,以为轨道线路设计或线路改造提供更多的参考依据。
1 单轮对轨道有限元模型
1.1 单轮对模型
考虑到计算成本,本文采用单轮对轨道有限元模型,该模型为纯数值模型,可在时域内进行运算,模型中任意测点的时域振动信号都可以输出。为真实模拟轮轨间的相互作用,车轮和钢轨都采用实体单元,钢轨与轨道板之间的扣件连接考虑为线性问题,即连接部件满足胡克定律,采用弹簧阻尼单元。对于整体道床,道床板与道床基底设置为绑定约束,力可直接传递到隧道及土层,而两种浮置板轨道的力则分别通过板下橡胶垫和钢弹簧传递至道床基底,板下橡胶垫采用实体单元,钢弹簧采用弹簧阻尼单元。
本文中轮轨接触的法向力采用非线性赫兹接触理论进行描述,赫兹接触理论如式(1)所示,切向力采用摩擦系数准则描述。
(1)
式中:P(t)为轮轨间法向作用力,N;δZ(t)为轮轨接触点处弹性压缩量,m;G为轮轨接触常数,具体数值与车轮踏面外形有关,本文中为磨型踏面,对应的G=3.86R-0.115×10-8,m/N3/2,其中R为轮对半径,mm。
本文选取常用的美国六级谱(式(2))作为系统激励的轨道谱,并根据三角级数法[8]将轨道谱转换为空间样本输入到单轮对轨道有限元模型中。轨道不平顺一般分为高低、方向、轨距、水平4类,线路中的主要激励为垂向激励,因此单轮对轨道有限元模型将通过美国六级谱生成轨道线路中的高低不平顺。
(2)
式中:Sv(Ω)为轨道不平顺功率谱密度,cm2·rad/m;Ω为空间角频率,rad/m;Av为粗糙度系数;Ωc为截止频率,rad/m;k为影响系数,一般k取0.25。
1.2 单轮对模型基本参数
钢轨:采用实体单元模拟,弹性模量为2.1×1011N/m2,泊松比为0.3,密度为7.83×103kg/m3。扣件:采用弹簧阻尼单元模拟,沿线路纵向布置,间距为0.6 m。钢弹簧:采用弹簧阻尼单元模拟,浮置板下沿线路纵向布置间距为1.2 m,阻尼为7.5×104N·s/m。减振垫:浮置板下垫层厚度为0.2 m,阻尼为7.5×104N·s/m。土体:采用实体单元模拟,弹性模量为2×107N/m2。隧道壁:采用实体单元模拟,内径为6 m,弹性模量为3.25×1010N/m2。
模型中荷载工况为:仿真速度60 km/h,轮对轴重10 t。
在以上理论及参数基础上,分别建立普通整体道床、隔离式减振垫浮置板和钢弹簧浮置板3种轨道的仿真模型,如图1所示。在轮对荷载激励作用下,钢弹簧浮置板轨道的道床振动加速度云图如图2所示。
图1 仿真模型

图2 钢弹簧浮置板轨道道床振动仿真云图
2 模型验证
为验证仿真模型的准确性,将工况相近的整体道床实测数据与仿真模型输出结果进行倍频程对比。图3,4分别为实测和仿真结果倍频程图。图5为圆形隧道普通整体道床的实测现场图,其中钢轨测点布置在轨底上侧。

图3 普通整体道床实测结果
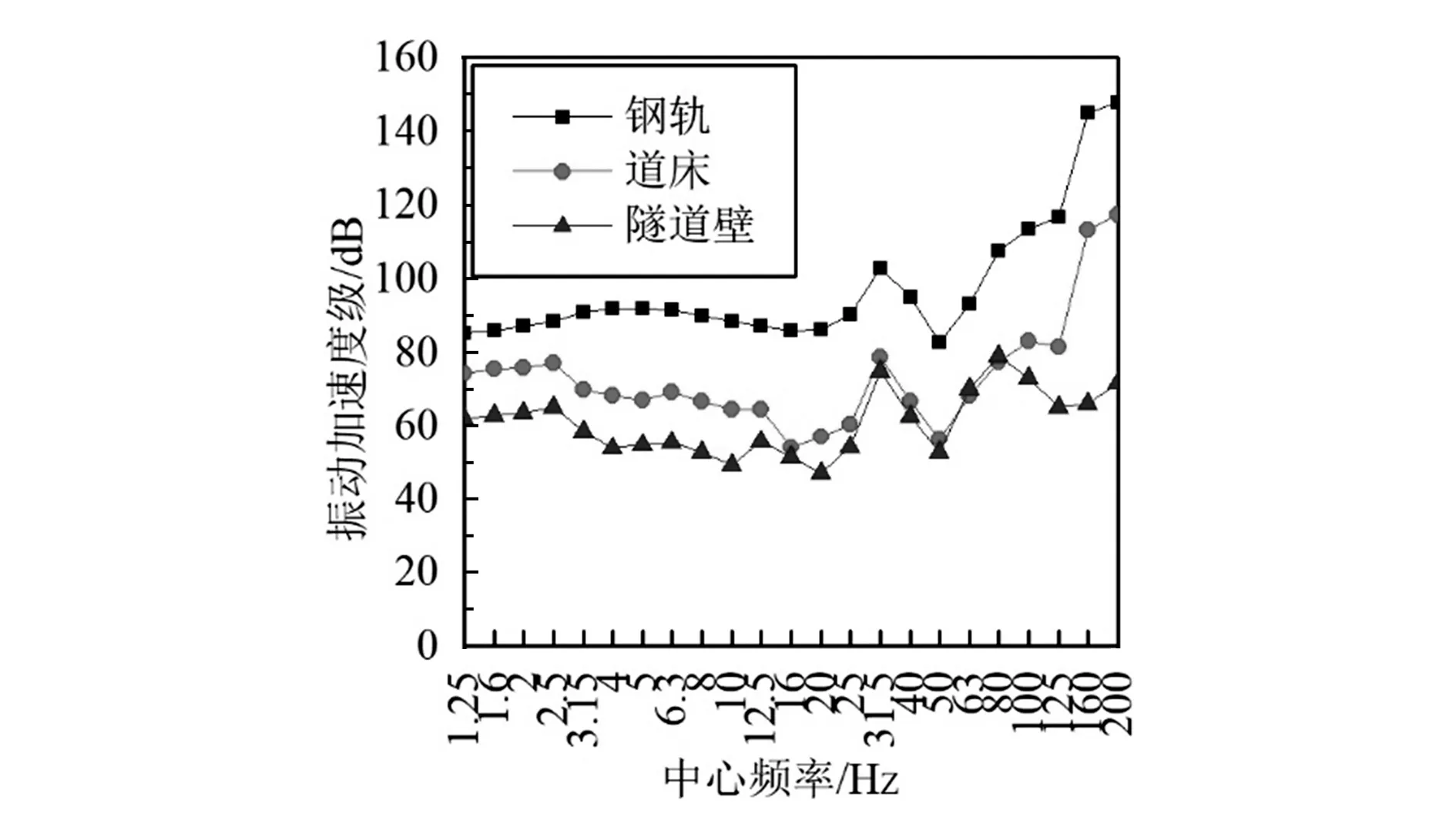
图4 普通整体道床仿真结果

图5 钢轨测点及实测现场
由图可以看出:钢轨测点的实测与仿真结果较为接近,振动加速度级随中心频率增大呈升高的趋势,且高频部分吻合较好;道床测点的实测与仿真结果在中低频段呈下降趋势,后随着频率增加振动加速度级升高,在40.00 Hz左右存在一个峰值,200.00 Hz左右两者的吻合性稍差;隧道壁测点的实测与仿真结果同样是在中低频段吻合性较好,在25.00~100.00 Hz之间,仿真结果波动较大,在100.00~200.00 Hz高频部分振动加速度级趋于一致。实测结果中振动加速度级变化具有连续性,而仿真结果的波动性较为明显,这可能是有限元计算中积分不稳定造成的。
总体来说,仿真结果能够较为真实地反映隧道内道床及隧道壁振动加速度级响应,依靠仿真模型分析轨道结构参数对隧道内总体结构振动的影响具有一定的可靠性。
3 轨道结构参数影响分析
3.1 扣件垂向刚度的影响
为研究扣件垂向刚度变化对地下轨道结构中道床及隧道壁振动加速度级的影响,参照工程中扣件刚度的设定范围,保持其他参数不变,对扣件刚度依次取20,30,40,50 kN/mm进行分析。
如图6,7所示,钢弹簧浮置板线路中,随扣件刚度增大,道床和隧道壁振动加速度级出现较为明显的差异,其中道床加速度级在1.25~3.15 Hz、10.00~31.50 Hz两个频段内随扣件刚度增大而减小,且在10.00~31.50 Hz频段内该趋势更明显,其余频段内道床振动加速度级随扣件刚度增大有所减小;对于隧道壁,除1.20~3.15 Hz、10.00~31.5 Hz两个频段内振动加速度级随扣件刚度增大而减小外,其余频率段都增大。可见,对于钢弹簧浮置板线路,增大扣件刚度会在一定程度上降低中低频段内的道床及隧道壁振动加速度级,而在高频段振动加速度级会增强。如图8,9所示,减振垫浮置板线路中,道床振动加速度级在20.00~31.50 Hz频段内随扣件刚度的增加而减小,在4.00~16.00 Hz频段内增大,此外高频段振动加速度级略微增加,低频振动加速度级变化不明显;对于隧道壁,随扣件刚度增加而振动加速度级降低的频率段为1.25~2.50 Hz及20.00~31.50 Hz,其余频段均增大。由此可见,随扣件刚度增大,减振垫浮置板线路中的道床及隧道壁在高频段(100.00~200.00 Hz)的振动加速度级增大,中低频(4.00~50.00 Hz)道床及隧道壁的振动加速度级值变化幅度大,对刚度变化较为敏感,超低频(0.00~4.00 Hz)振动无明显变化。如图10,11所示,整体道床线路中,道床测点在20.00~31.50 Hz频段内的振动加速度级随扣件刚度增大而减小,超低频段范围内基本不变,而高频段有所增加;隧道壁测点在超低频段(1.25~2.50 Hz)的振动加速度级随扣件刚度增加呈降低的趋势,4.00 Hz处对刚度的变化最为敏感,随扣件刚度增大振动加速度级增大明显。
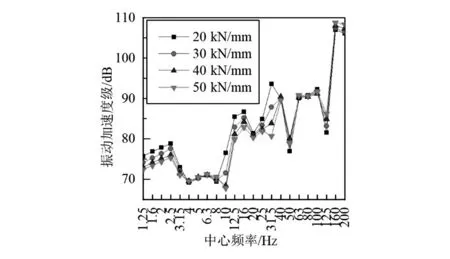
图6 垂向刚度对钢弹簧浮置板-道床的影响
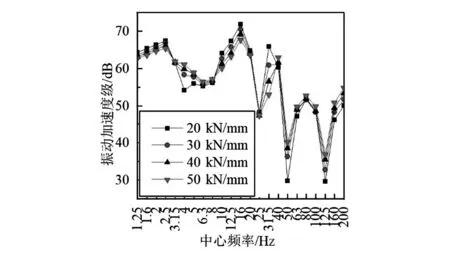
图7 垂向刚度对钢弹簧浮置板-隧道壁的影响
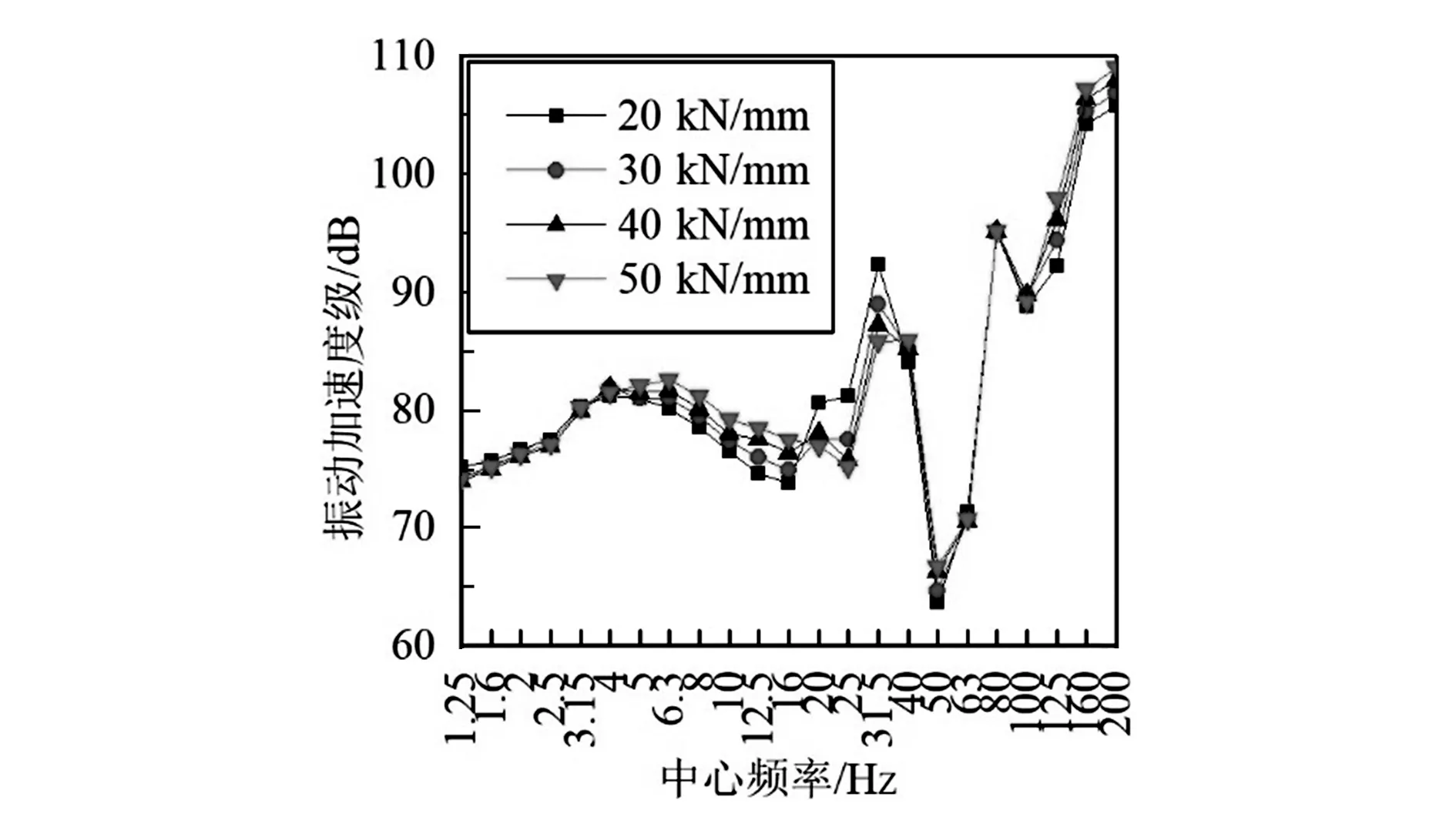
图8 垂向刚度对减振垫浮置板-道床的影响
对比分析3种轨道结构,增大扣件刚度,两种浮置板轨道在100.00 Hz以上的较高频段产生的振动会增大,而普通整体道床轨道的振动则是在40.00~100.00 Hz中低频范围内增大。随扣件刚度的增大,3种轨道结构的道床振动在25.00~31.50 Hz频率范围内的振动都有所减小,钢弹簧浮置板轨道道床在16.00 Hz以下的低频范围内振动有所减小,而减振垫浮置板轨道则是增大。对比分析隧道壁测点,轨道结构振动在16.00~31.50 Hz频段内随扣件刚度增加而减小,在3.15~8.00 Hz和40.00~200.00 Hz频段内随扣件刚度增加而增大,可以观察到,整体道床轨道隧道壁测点的振动加速度级的变化最为明显,这是因为整体道床主要依靠扣件减振,扣件刚度增加会使得大部分振动能量直接传递到隧道壁。
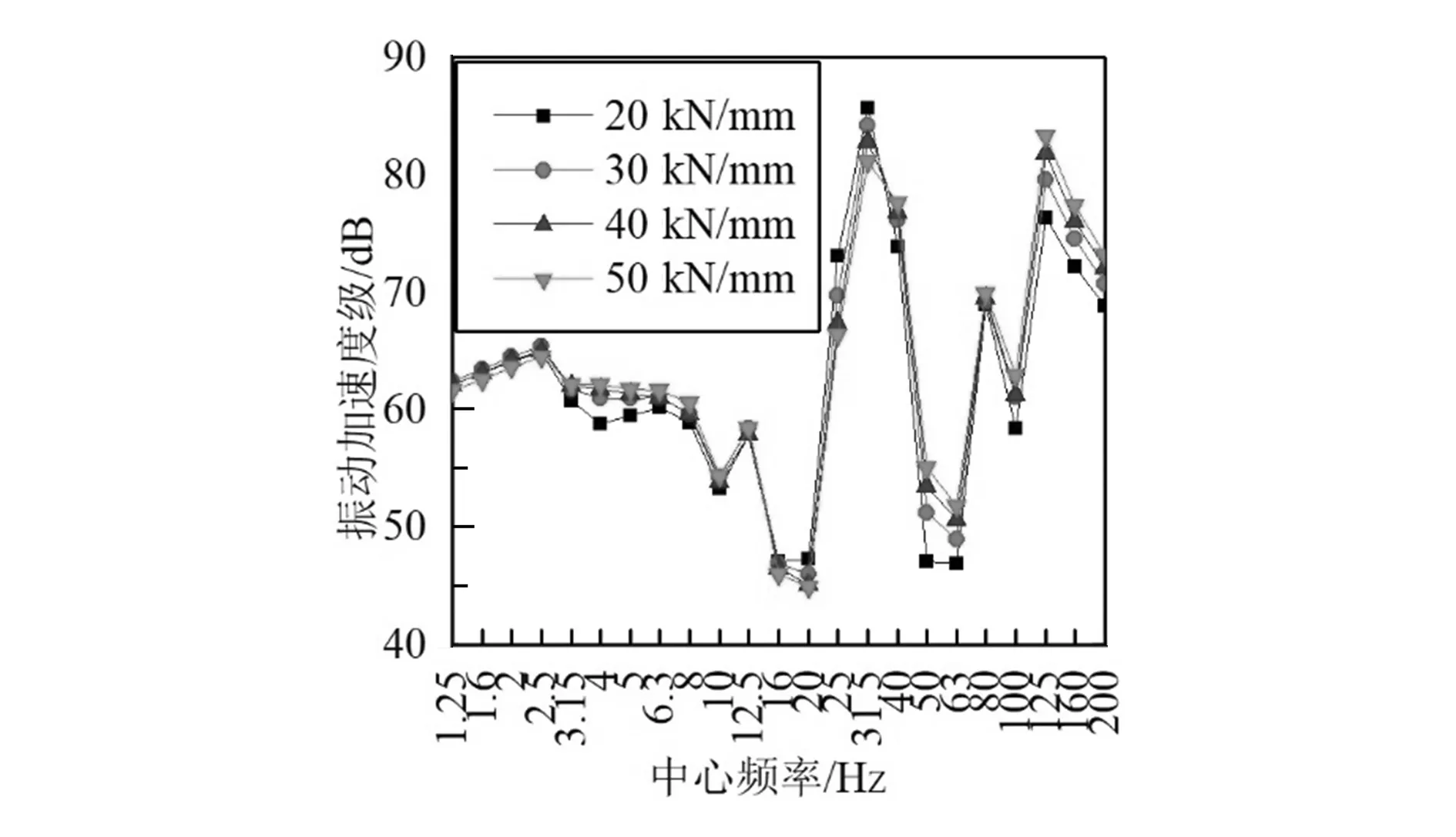
图9 垂向刚度对减振垫浮置板-隧道壁的影响
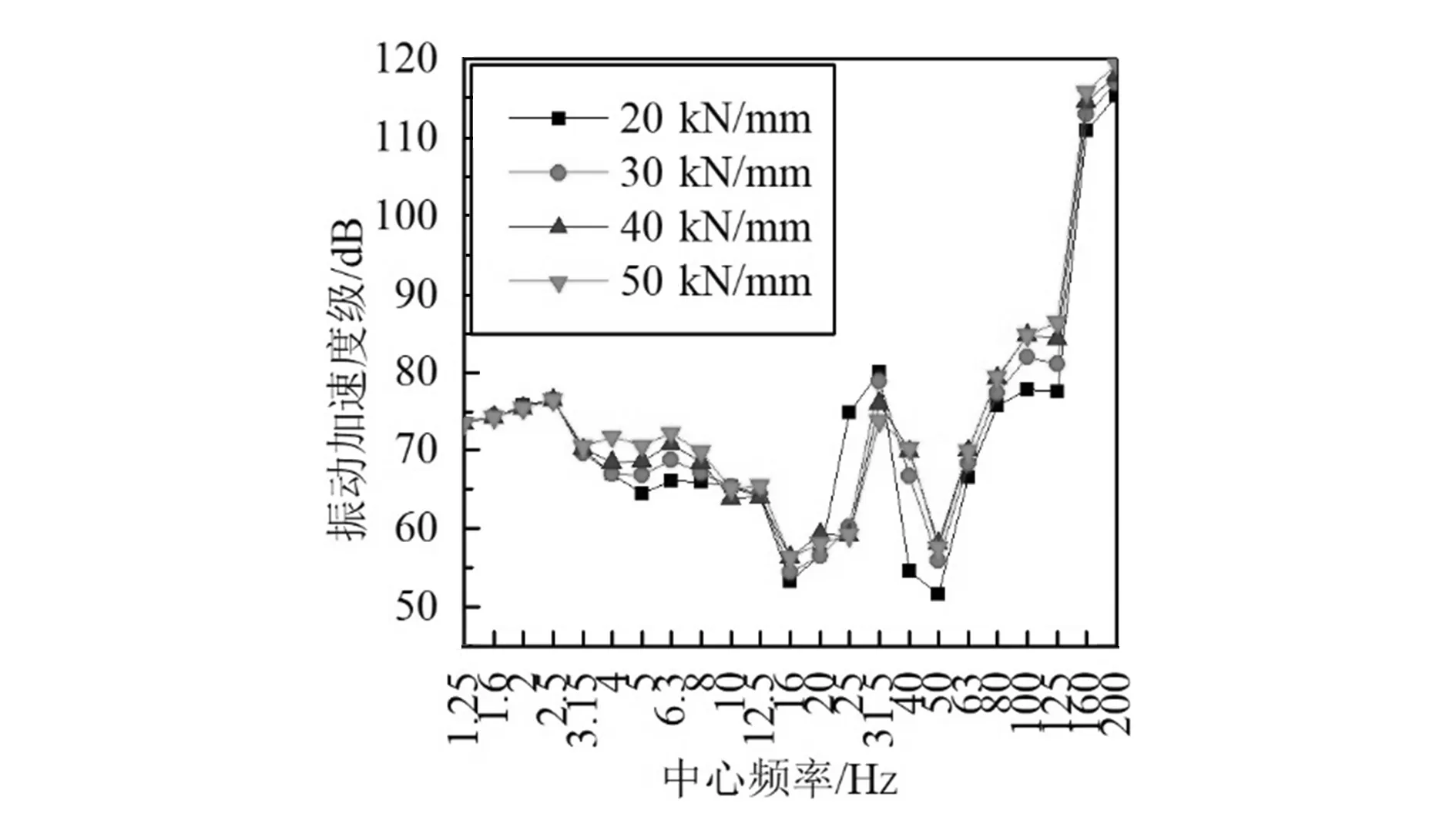
图10 普通整体道床-道床
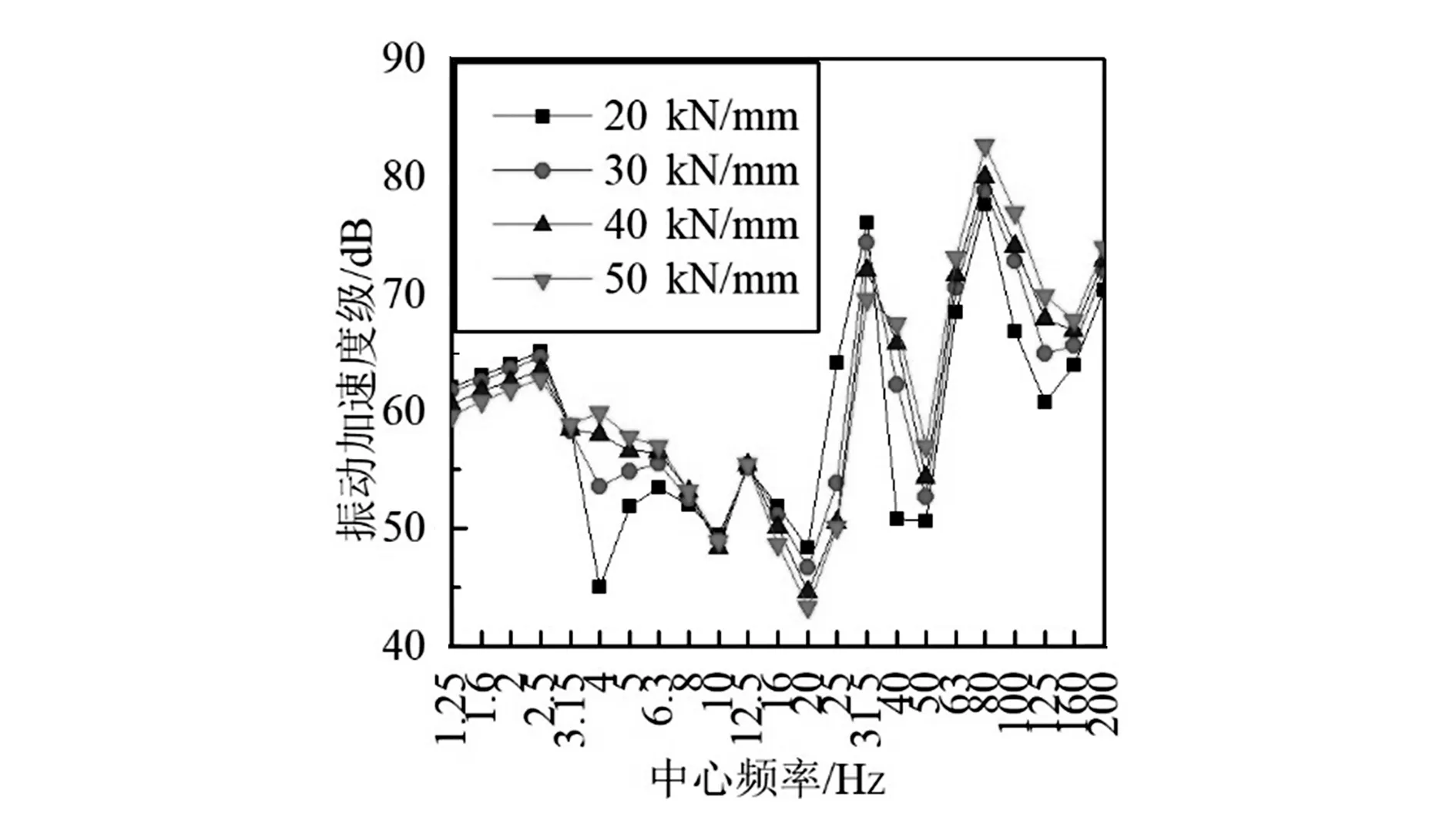
图11 普通整体道床-隧道壁
3.2 支座刚度的影响
在工程中,钢弹簧浮置板和减振垫浮置板是比较常用的两类浮置板轨道系统,其中钢弹簧浮置板因支座刚度小且具备更小的自振频率,减振效果较好,而减振垫浮置板减振效果次之,本文中对钢弹簧浮置板支座刚度工况取值从5 kN/mm依次增加到35 kN/mm,减振垫浮置板支座刚度依次从20 kN/mm增加到50 kN/mm。
分析图12,13可知,在钢弹簧浮置板线路中,道床测点振动加速度级在200.00 Hz以内随支座刚度的增加而减小,其中200.00 Hz时减小幅度最为明显,达39.60 dB;支座刚度从5 kN/mm增加到15 kN/mm时道床振动减弱最明显,因此该刚度区间可能为敏感区间。对于隧道壁,在1.25~8.00 Hz和25.00~200.00 Hz频段内随支座刚度的增加其测点振动增大,其中25.00 Hz时增大值最大,为15.46 dB,隧道壁测点频谱特征未发生明显改变。分析图14,15可知,减振垫浮置板轨道中的道床振动加速度级随支座刚度增大而减小,且在6.30~25.00 Hz时减小幅度最为明显,20.00 Hz时达到9.50 dB;隧道壁测点振动加速度级在31.50~100.00 Hz时随支座刚度增大而增大,在31.50 Hz时最大,为10.94 dB。

图12 支座刚度对钢弹簧浮置板-道床的影响
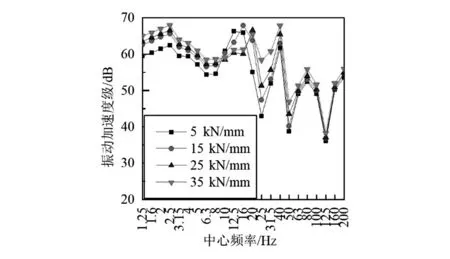
图13 支座刚度对钢弹簧浮置板-隧道壁的影响

图14 支座刚度对减振垫浮置板-道床图的影响

图15 支座刚度对减振垫浮置板-隧道壁的影响
对比两种浮置板轨道,在支座刚度增加的情况下,钢弹簧浮置板轨道中的道床振动加速度级在200.00 Hz频段内都是减小的,而减振垫浮置板道床振动加速度级仅在6.30~25.00 Hz频率段以内减小较为明显;对于隧道壁测点,随着支座刚度的增加,隧道壁振动加速度级在200.00 Hz以内几乎都是增加的,而减振垫浮置板轨道振动加速度级增加较为明显的频段为31.50~100.00 Hz。总结可知,改变支座刚度,对钢弹簧浮置板轨道影响的频段更宽,而对减振垫浮置板的影响主要表现在中低频。
4 结束语
本文通过建立单轮对有限元模型,分析了不同轨道结构中扣件刚度、板下支座刚度这两个参数的变化对隧道结构振动的影响,结果表明无论是增加扣件垂向刚度还是支座刚度,都会引起道床和隧道振动倍频程中某一频率段发生较为明显的振动加速度级变化,因此在实际工程运用中有必要考虑因扣件和支座刚度变化带来的振动特征变化,以降低工程成本。本文针对扣件刚度和支座刚度,只考虑了其垂向刚度的变化,而在实际工程中横向刚度也是维持线路处于平顺状态的重要参数,横向参数的影响同样具备一定的研究价值。

