2-UPS/RRP调心式髋关节康复机构的运动学及性能分析
杨 路,李瑞琴,刘荣帅,马世豪
(中北大学机械工程学院,山西 太原 030051)
并联机构具有承载力高、运动精度高和反解计算较容易等优点[1]。将少自由度并联机构用于髋关节康复有利于简化结构、避免干涉、方便控制。刘芳芳[2]利用螺旋理论对3-UPS/RRR并联脚踝康复机构进行了自由度的求解。李剑锋等[3]使用解析法对一种髋关节助力机构进行了位置反解,并建立了速度雅克比矩阵。杨亚敬等[4]利用仿生关节空间与机构工作空间的映射关系求解了3-RRR+(S-P)球面髋关节机构的位置正反解。马世豪等[5]对2-SPR/RUPR并联机构进行了逆运动学和可达工作空间的求解。Wu等[6]针对现有髋关节患者设计了一种下肢康复机构。陈荣[7]将一种3-RRR+S仿生球面并联机构应用于人体髋关节。Wang等[8]对一种新型3-PUU并联机构进行了优化设计。朱灿一[9]研究了一种3-SPS并联仿生髋关节的动力学。贺鑫[10]对3-UPU髋关节康复机构进行了动力学分析和康复仿真。Schreiber等[11]提出一种2(RPR)-2(RPR)R并联机构并分析了其运动学性能。祖永芳[12]基于模糊PID控制器对一种下肢康复机器人的运动学进行了分析,进而搭建了康复控制系统。
现有髋关节康复机构的研究已取得不少成果,但仍存在一些缺陷,例如:机构自由度不足或冗余、机构旋转中心与人体髋关节旋转中心不一致、机构过于复杂导致患者穿戴体验较差等。本文提出一种可调心的2-UPS/RRP并联康复机构,其可穿戴于不同体型的髋关节患者并能保证人机转动中心的一致性,使得康复过程更安全。
1 2-UPS/RRP髋关节康复机构及调心原理
1.1 2-UPS/RRP髋关节康复机构构型
如图1所示,2-UPS/RRP髋关节康复简化模型由静平台、2条UPS支链(驱动支链UPS-I和驱动支链UPS-Ⅱ)、3条约束支链(约束支链R-Ⅰ、R-Ⅱ、R-Ⅲ)、支撑驱动杆以及动平台组成。

图1 2-UPS/RRP髋关节康复机构简化模型
2-UPS/RRP康复机构整体模型如图2所示,机构静平台与腰部固定装置通过3套调心组件2连接,腰部固定装置与其内侧的充气衬垫相连,两者之间是调心组件1。2个U副、约束支链R-I和R-Ⅱ均通过连接槽与静平台相连。支撑驱动杆上端通过转动副与约束支链R-Ⅲ相连,下端通过移动副与动平台相连。腿部夹紧装置固连于环形滑块。腿部夹紧装置和腰部衬垫均采用柔性环保材料,以保证康复过程中人体的安全和舒适。
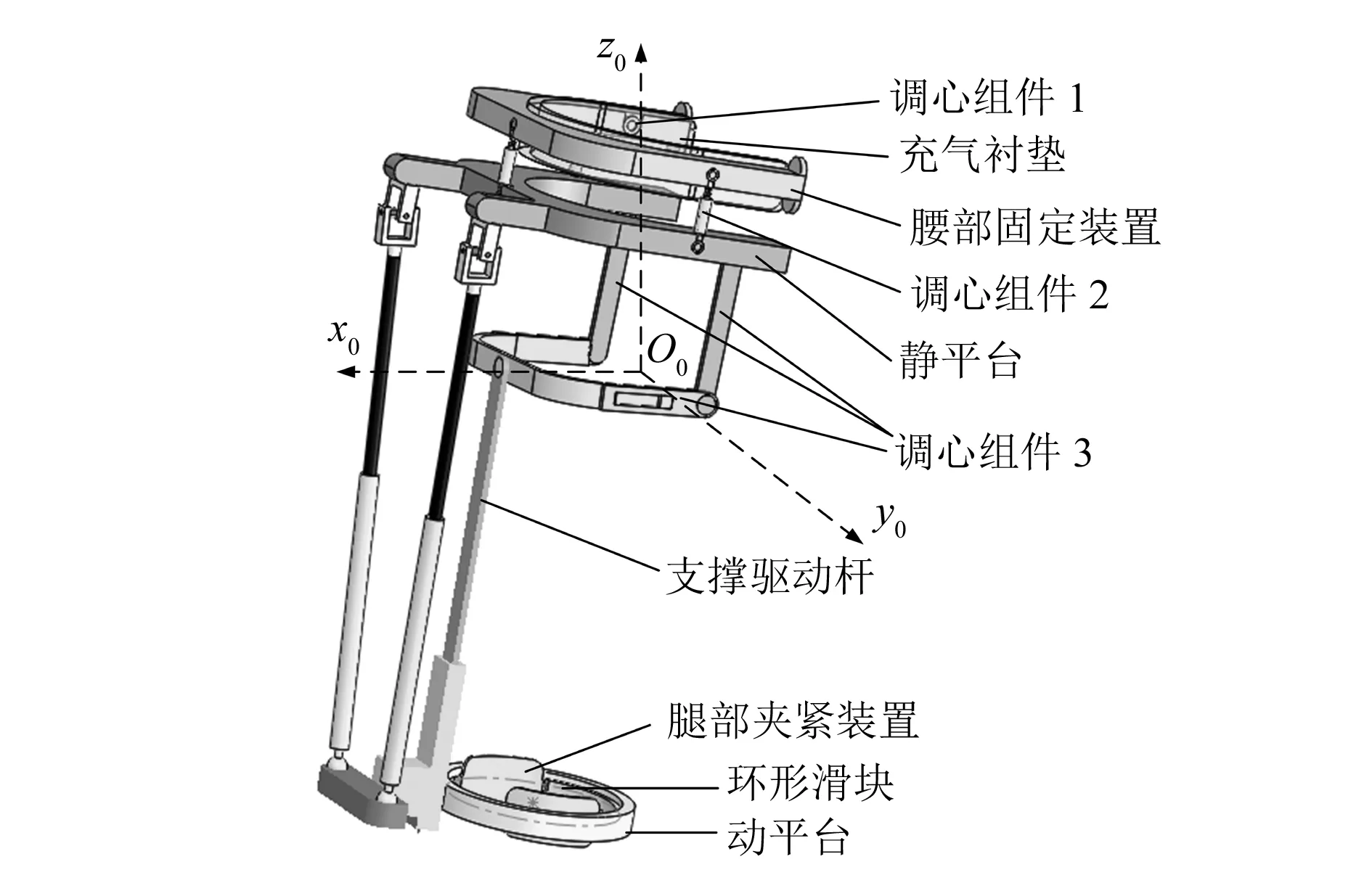
图2 2-UPS/RRP康复机构整体模型
1.2 2-UPS/RRP髋关节康复机构调心原理
髋关节康复机构有3套调心组件。调心组件1由腰部固定装置内侧的凹槽和不同厚度规格的垫片组成。凹槽有2个,分别位于人体背部和腹部,通过添加垫片可以调节充气衬垫与腰部固定装置的前后相对位置,即可调节机构旋转中心在y轴的坐标。调心组件2由螺纹调节柱、与腰部固定装置相连的右旋螺纹杆和与静平台相连的左旋螺纹杆组成。转动3个调节柱可整体改变腰部固定装置与静平台在竖直方向相对位置,即可调节机构旋转中心在z轴的坐标。调心组件3由3条约束支链和静平台组成。改变约束支链R-I和R-Ⅱ在静平台底端连接槽中的位置以及约束支链R-Ⅲ的长短,可调节机构旋转中心在x轴的坐标。

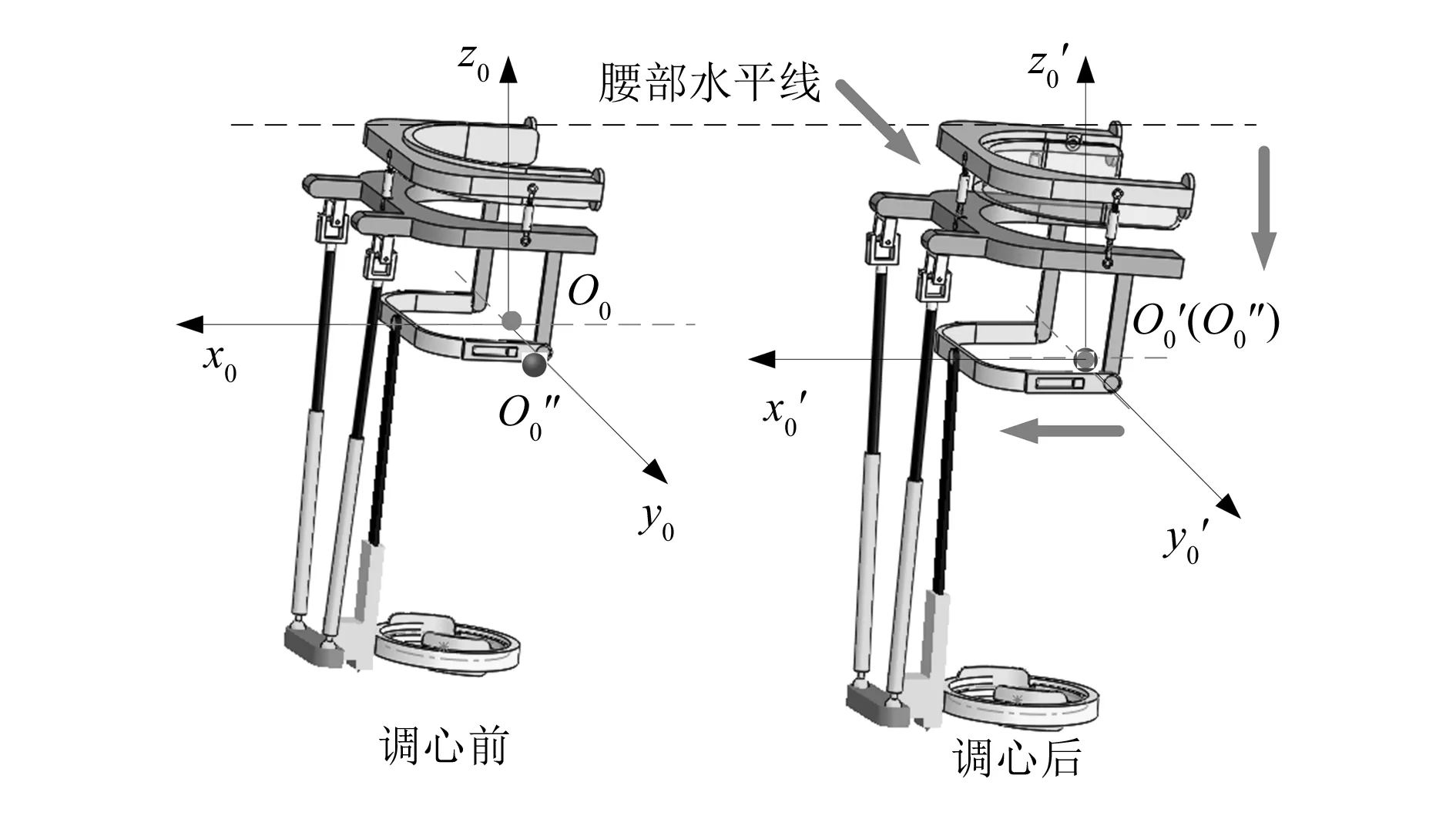
图3 2-UPS/RRP髋关节康复机构调心原理
机构一共有2种运动模式,主动模式下患肢可进行前屈/后伸和内收/外展以及牵伸运动,被动模式下患者可进行内旋/外旋运动。以机构安装在人体右腿为例:约束支链R-Ⅰ、R-Ⅱ与R-Ⅲ无相对转动的情况下,令UPS-Ⅰ伸长、UPS-Ⅱ缩短,此时机构带动下患肢实现前屈运动,反之为后伸;R-Ⅲ与支撑杆无相对转动的情况下,UPS-Ⅰ和UPS-Ⅱ同时缩短时患肢外展,同时伸长时患肢内收,UPS-Ⅰ、UPS-Ⅱ和支撑驱动杆同时伸长或缩短实现机构的牵伸运动。被动模式下,人腿主动进行内旋/外旋动作,带动夹紧装置与环形滑块在动平台配合槽中旋转。
2 2-UPS/RRP髋关节康复机构自由度分析
采用螺旋理论分析2-UPS/RRP髋关节康复机构的自由度。采用运动副螺旋表示机构的运动副,不同的运动副螺旋组成机构的运动螺旋系。先取支链UPS-Ⅰ进行研究,建立支链坐标系O1-x1y1z1,初始位置时,x1轴平行于U副第二根轴线,y1轴沿水平面指向正前方,z1轴符合右手规则,如图4所示。图中$11,$12,$13分别表示支链底端球副沿x,y和z轴的运动螺旋;$14表示支链中间移动副的运动螺旋;$15和$16分别表示支链上端U副沿x轴和y轴的运动螺旋。
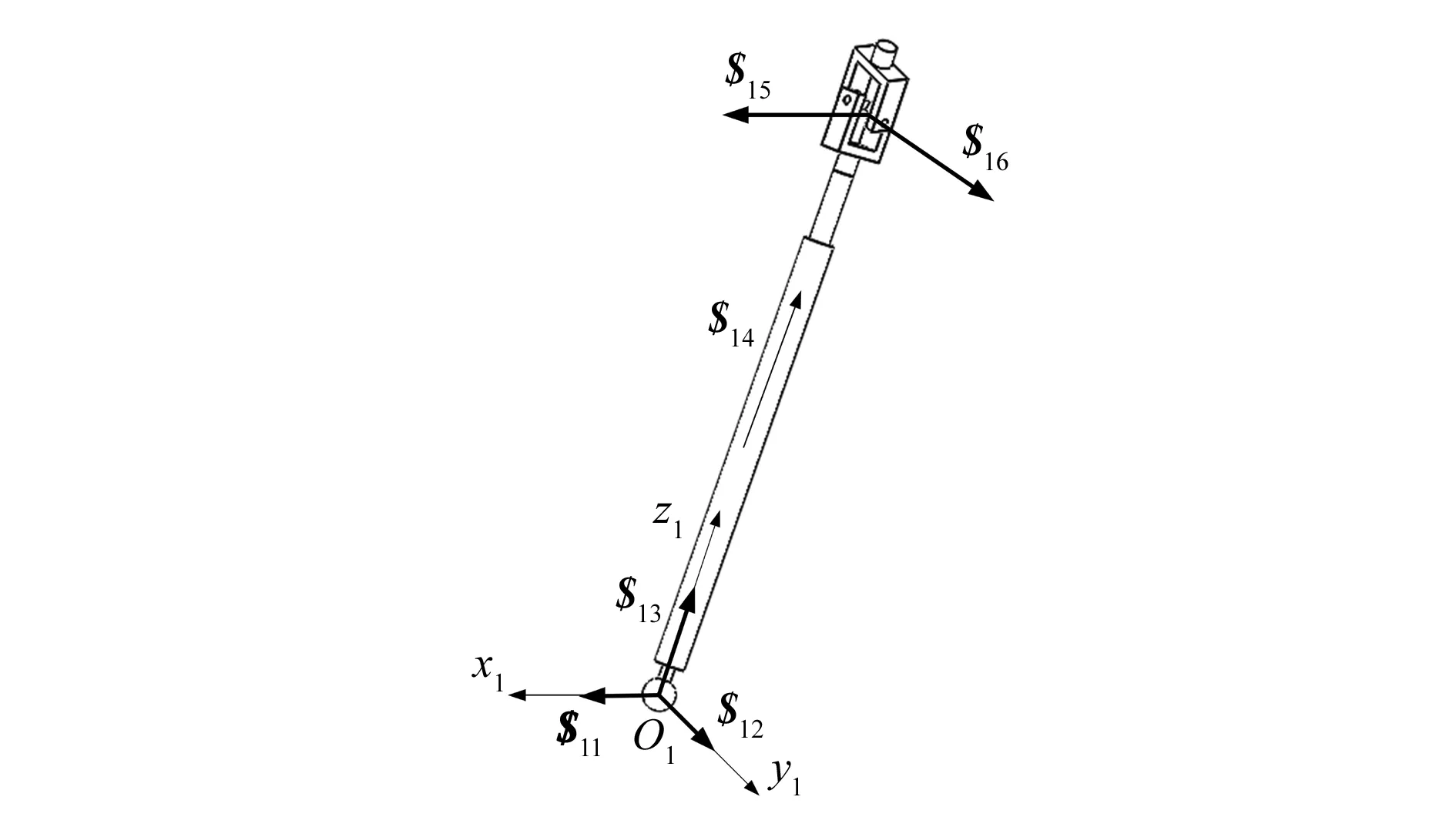
图4 UPS支链螺旋坐标系
可得UPS-I支链的螺旋系为:
$11=(1 0 0;0 0 0)
$12=(0 1 0;0 0 0)
$13=(0 0 1;0 0 0)
$14=(0 0 0;0 0 1)
$15=(1 0 0;0L0)
$16=(0 1 0;-L0 0)
(1)
式中:L为球副与U副之间的距离。
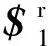
(2)
解得:
(3)
由此可以看出,UPS-I支链的6个螺旋线性相关,因此该支链对动平台不产生约束。由于2条UPS支链对称分布且结构相同,故UPS-Ⅱ也不产生约束。
再取3根约束支链进行研究,建立支链坐标系O2-x2y2z2。初始位置时,x2轴平行于U副第二根轴线,z2轴垂直向上,y2轴符合右手规则,如图5所示。图中$31,$32分别表示3根约束支链中2个转动副的螺旋。
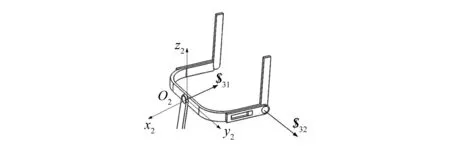
图5 约束支链螺旋坐标系
$31=(-1 0 0;0 0 0)
$32=(0 1 0;-a0 0)
(4)
由式(4)求得约束支链螺旋系的反螺旋为:
(5)

(6)
式中:由于该机构没有公共约束,所以机构的阶数d=6;n为包括机架在内的构件数目;g为机构中运动副的数目;fi为第i个运动副的自由度数;ν为机构中的冗余约束,ν=0;ξ为机构中的局部自由度,ξ=0。综上所述,2-UPS/RRP髋关节康复机构具有3个主动自由度,可满足髋关节患者前屈/后伸、内收/外展以及牵伸的康复需求。
3 2-UPS/RRP髋关节康复机构的位置分析及逆解
2-UPS/RRP髋关节康复机构简图和驱动支链坐标系简图分别如图6和7所示。初始位置静坐标系和动坐标系分别为O-x0y0z0和P-xpypzp。O和P位于机构旋转中心。ai,bi,pi分别为原点在球副、U副和P副的移动距离。旋转中心所在平台与静平台距离为L1,与动平台距离为L2,U副第一根轴线与y0轴平行,第二根轴线与x0轴平行。ai-xaiyaizai和bi-xbiybizbi分别表示原点在球副、U副中心的坐标系,且2个坐标系的坐标轴平行。xbi和ybi分别与U副第二、第一根轴线平行,zbi符合右手规则。坐标系ci-xciycizci中,原点ci与bi重合,yci与U副第一根轴线平行,zci平行于cidi,xci可用右手规则判断。驱动支链1和2绕U副两根轴线的转角分别表示为qi1和qi2。

图6 2-UPS/RRP髋关节康复机构简图
动平台的姿态用欧拉角描述,用α表示绕x轴即前屈/后伸的角度,β表示绕y轴即外展/内收的角度。于是2-UPS/RRP髋关节康复机构的位置逆解为已知动平台的输出参数α和β,求解UPS支链的输入参数qi1和qi2。图7为UPS支链坐标系简图。
机构动平台相对于静平台的旋转矩阵ROP可以表示为α的旋转矩阵Rα和β的旋转矩阵Rβ的乘积:

图7 驱动支链坐标系简图
ROP=RαRβ
(7)
球副中心Oai的位置矢量可表示为:
Oai=rP+ROPrpai
(8)
式中:rP为动坐标系原点P点在静坐标系中的位置矢量;rPai为铰链ai相对于动坐标系原点P的位置矢量。进一步得到:
Oai=aizci+rbi=aiROci(0,0,1)T+rbi
(9)
式中:ai为P副中心点的移动距离;zci为坐标系ci-xciycizci的z轴向量;rbi为铰链bi在静坐标系中的位置矢量;ROci为静坐标系O-x0y0z0到坐标系ci-xciycizci的变换矩阵。
坐标系bi-xbiybizbi到ci-xciycizci的变换矩阵Rbici可表示为:
(10)
由式(8)和(9)可得:
ai=|rP+ROPrPai-rbi|
(11)
由式(9)到(11)可得
(12)

令式(12)右侧矩阵中3行分别等于xi1,xi2,xi3,可得:
(13)
由此求出2-UPS/RRP髋关节康复机构的位置逆解。
4 2-UPS/RRP髋关节康复机构工作空间
采用三维空间搜索法求解2-UPS/RRP髋关节康复机构的工作空间,设定机构参数,见表1。

表1 2-UPS/RRP髋关节康复机构的机构参数
在驱动支链UPS-Ⅰ、UPS-Ⅱ和支撑驱动杆上分别安装线性驱动马达。将数据点导入驱动马达,进行Motion分析后得出动平台输出轨迹的坐标文件。将文件导入软件MATLAB中,采用plot函数绘制出2-UPS/RR髋关节康复机构的工作空间,如图8所示。
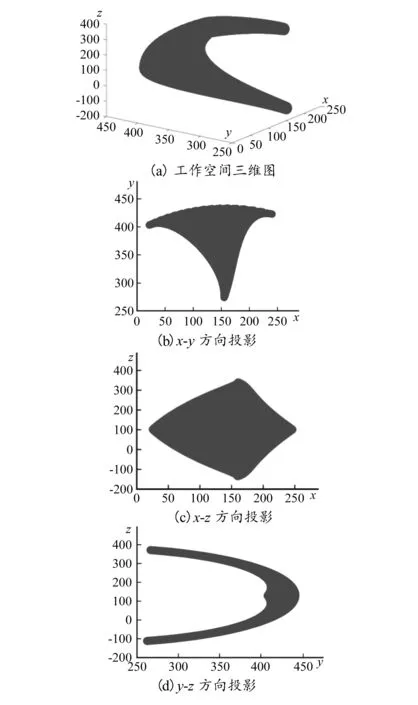
图8 2-UPS/RRP髋关节康复机构的工作空间
由图可知,机构工作空间呈实心曲面状,表明在此空间内运动时不存在奇异位型。机构工作空间关于x轴对称,表明前屈/后伸的工作空间相同;工作空间关于y轴不对称,表明机构的内收范围小于外展范围。
5 髋关节康复实例
将机构模型导入动力学仿真软件ADAMS中,添加约束后,采用step函数驱动UPS支链并进行仿真,图9、图10分别为机构进行前屈/后伸和内收/外展时动平台转动角位移和角速度随时间的变化曲线。
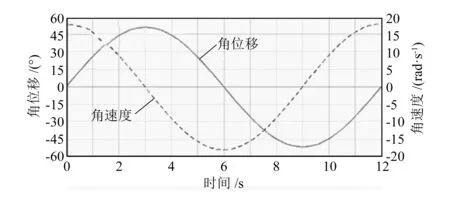
图9 机构前屈/后伸角位移和角速度曲线
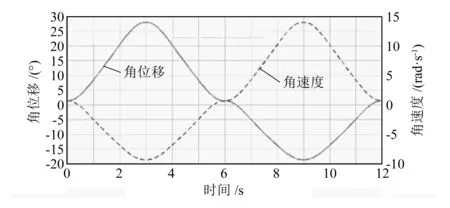
图10 机构内收/外展角位移和角速度曲线
由图可以看出,2-UPS/RRP髋关节康复机构在前屈/后伸运动中角度均达到了58°,在内收/外展运动中角度分别达到了19°和28°,两种运动仿真中角位移和角速度曲线光滑连续,表明康复过程稳定可靠,不存在速度和力的突变。
6 结束语
本文提出了一种可调心式2-UPS-RRP并联髋关节康复机构,用于不同体型患者进行康复训练。基于螺旋理论求得机构具有2个转动自由度和1个移动自由度。采用位置矢量法求出了机构的位置逆解。利用三维动态求得机构的工作空间呈实心曲面状。ADAMS仿真结果表明,机构的前屈/后伸、内收/外展角度分别可达58°、58°、19°、28°,可满足髋关节患者的康复需求,机构动平台的角位移、角速度曲线光滑连续,表明康复过程安全平稳。未来可从动力学入手,进一步优化机构的运动性能。

