新型RSCS-RSSR空间转舵机构的设计及分析
胡红宇,陈 勇,桑胜亚
(上海大学机电工程与自动化学院,上海 200072)
船舶作为海洋航行的主要交通工具,其最重要的执行器为舵机。舵机主要由远距离操纵机构、转舵动力机械和转舵机构组成,而高精度、高可靠性的转舵机构对于船舶的灵活性与安全性有着相当重要的意义。
陈正泉[1]对比了传统电液舵机的转舵机构——摆缸式、转叶式和拨叉式转舵机构,这3种转舵机构都是将液压系统与机械机构组合,达到舵叶偏转的目的;王俊全等[2]设计了一种新型的四轴联动舵机机构;鲍文亮[3]提出了由直流电机驱动、锥齿轮变向的舵机系统整体设计方案;祝川等[4]设计了以曲柄滑块机构为基础的电液伺服舵机系统,该机构将液压缸活塞杆等效为滑块,喷泵的喷嘴等效为曲柄;葛明[5]设计了以空间曲柄摇杆机构(RSSR)作为舵机的执行机构,以1台电动机驱动4片舵翼,极大减小了舵机的体积。
空间机构由于具有结构紧凑、运动灵活多样的特点,因此常应用于航空、船舶舵机系统,然而空间机构的分析要比平面机构复杂困难得多。常用的分析方法有以几何为基础的图解法,以及运用对偶数、向量和矩阵等数学工具的解析法。随着计算机技术的普及应用,解析法得到了迅速发展,并已成为空间连杆机构研究和解算的基本方法。
本文针对喷泵推进系统,提出一种新型空间转舵机构。首先在SolidWorks中建立1∶1三维模型, 然后根据方向余弦矩阵法[6]求解机构输入输出位移方程,最后在运动副处建立静力平衡方程,求解各约束反力。
1 转舵机构的三维模型
如图1所示,在SolidWorks中建立转舵机构1∶1三维实体模型,该机构可以等效为空间摆动缸机构(RSCS)和RSSR连接而成的组合机构,考虑到船舱内布局和防水问题,RSCS布置在船舱内,RSSR布置在船舱外,二者之间由一根固连的传力杆进行传动。
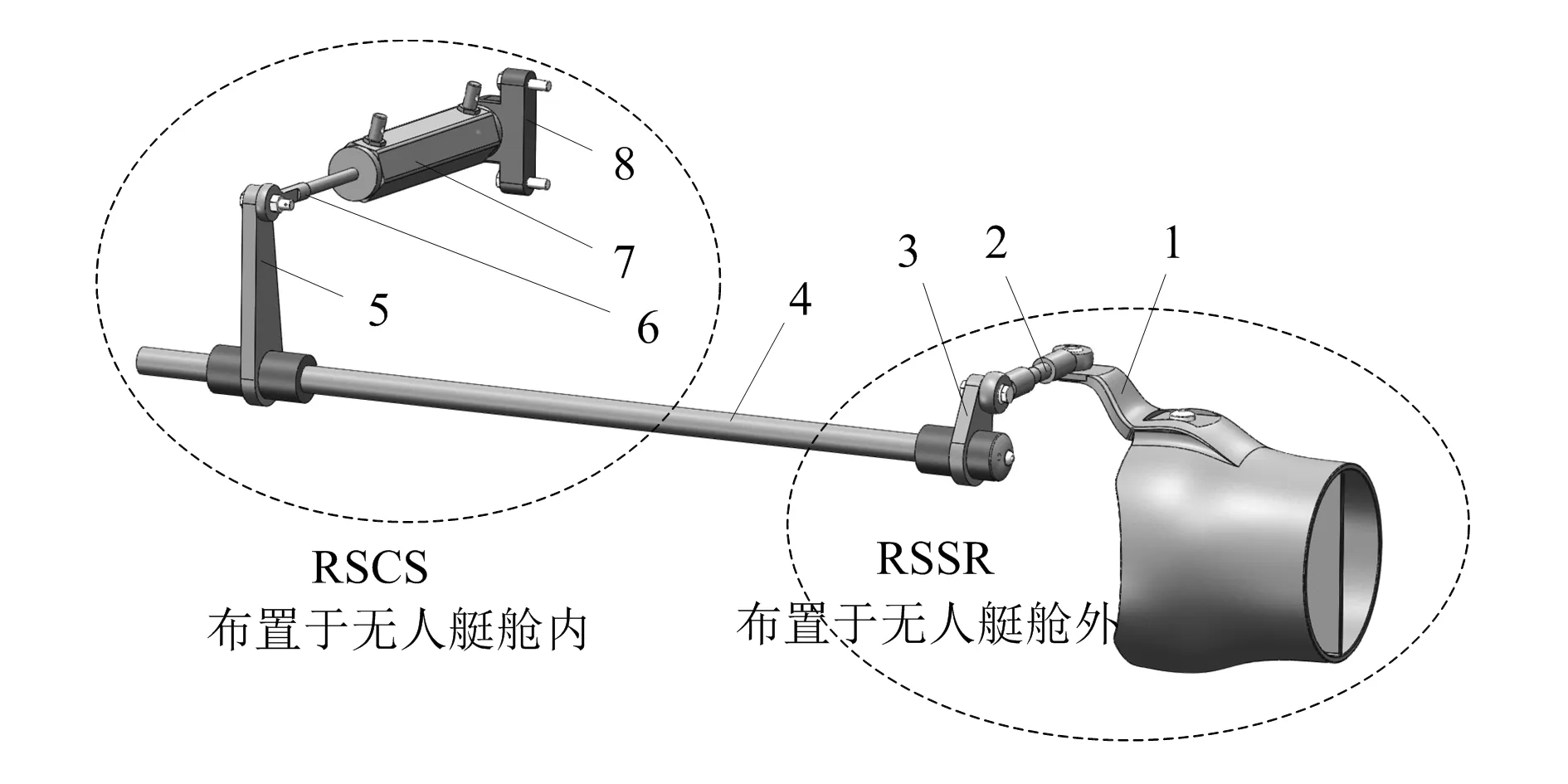
1—喷嘴;2—中间连杆;3—输入曲柄;4—传力杆;5—摇杆;6—活塞杆;7—液压缸;8—机架
如图1 所示,RSCS由液压缸、活塞杆、摇杆、固连在机架上的球面副(S)和转动副(R)、活塞杆与液压缸之间的圆柱副(C)、活塞杆与摇杆之间的球面副(S)构成,其中摇杆与传力杆固连在一起,将运动和力矩传递给空间曲柄摇杆机构; RSSR由喷嘴、中间连杆、输入曲柄、两个固连在机架上的转动副(R)、连杆两端的球面副(S)构成。图中喷嘴可以等效为摇杆,绕机架在水平面内转动。
2 RSSR分析
2.1 RSSR运动分析
如图2所示,使用拆杆法将连杆2假想拆离,建立曲柄输入角θ1和摇杆输出角θ3的关系式,按照右手笛卡尔坐标系规则,设置3个坐标系。z1轴和z3轴分别取沿曲柄1和摇杆3的转动轴线,而与机架相固结的z0轴与z1轴重合;x1轴与过球面副中心B所作z1轴的垂线相重合,x3轴与过球面副中心C所作z3轴的垂线相重合,x0轴取z1和z3两轴线的公垂线方向。正对z3轴观察时输出角θ3为x3轴逆时针方向转至z0轴的转角。图中已知结构参数为:h1=AB,l=BC,h3=DC,s3=DD′,s0=AA′,h0=A′D′。
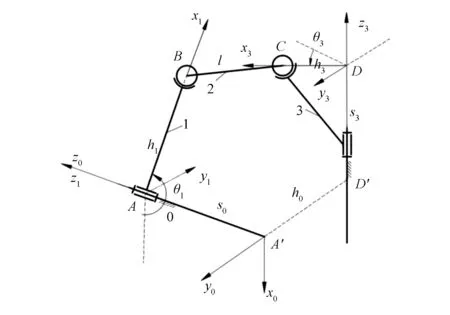
图2 RSSR简图
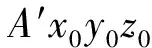
(1)
(2)
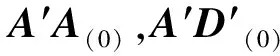
机构在运动时,杆长l不变,可得:
(xB-xC)2+(yB-yC)2+(zB-zC)2=l2
(3)
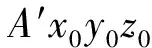
将式(1)、(2)代入式(3)并整理,可得机构的输入输出方程如下:
Lsinθ3+Mcosθ3+N=0
(4)
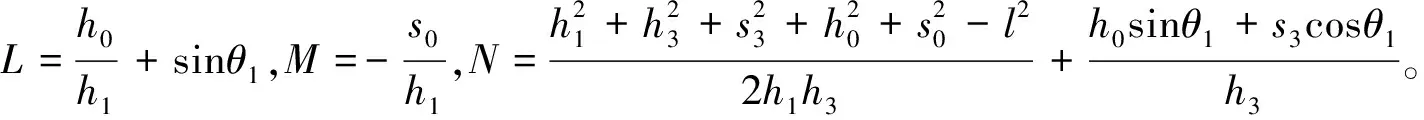
利用正切半角公式求解式(4),可得输出角θ3的表达式:
(5)
式中的正负号与机构的实际位置有关,在本文机构中取负号。
2.2 RSSR静力分析
低速运行且质量较轻的机构,其惯性力通常较小,常常忽略不计,只需对这类机构作静力分析,可大大简化模型,有利于复杂系统的求解。
中间连杆为二力杆,球面副中约束反力的作用线沿两个球面副中心B、C的连线,大小待定。以Dx3y3z3为参考坐标系,连杆2作用在摇杆3上的约束反力R23在x,y,z轴向的分量R23x,R23y,R23z为:
(6)
式中:(xB3,yB3,zB3)、(xC3,yC3,zC3)分别为B、C两点在Dx3y3z3坐标系下的坐标,其中xC3=h3,yC3=0,zC3=0。
(7)
摇杆3的受力分析如图3(a)所示,根据摇杆3的力平衡和力矩平衡关系,可得:
(8)
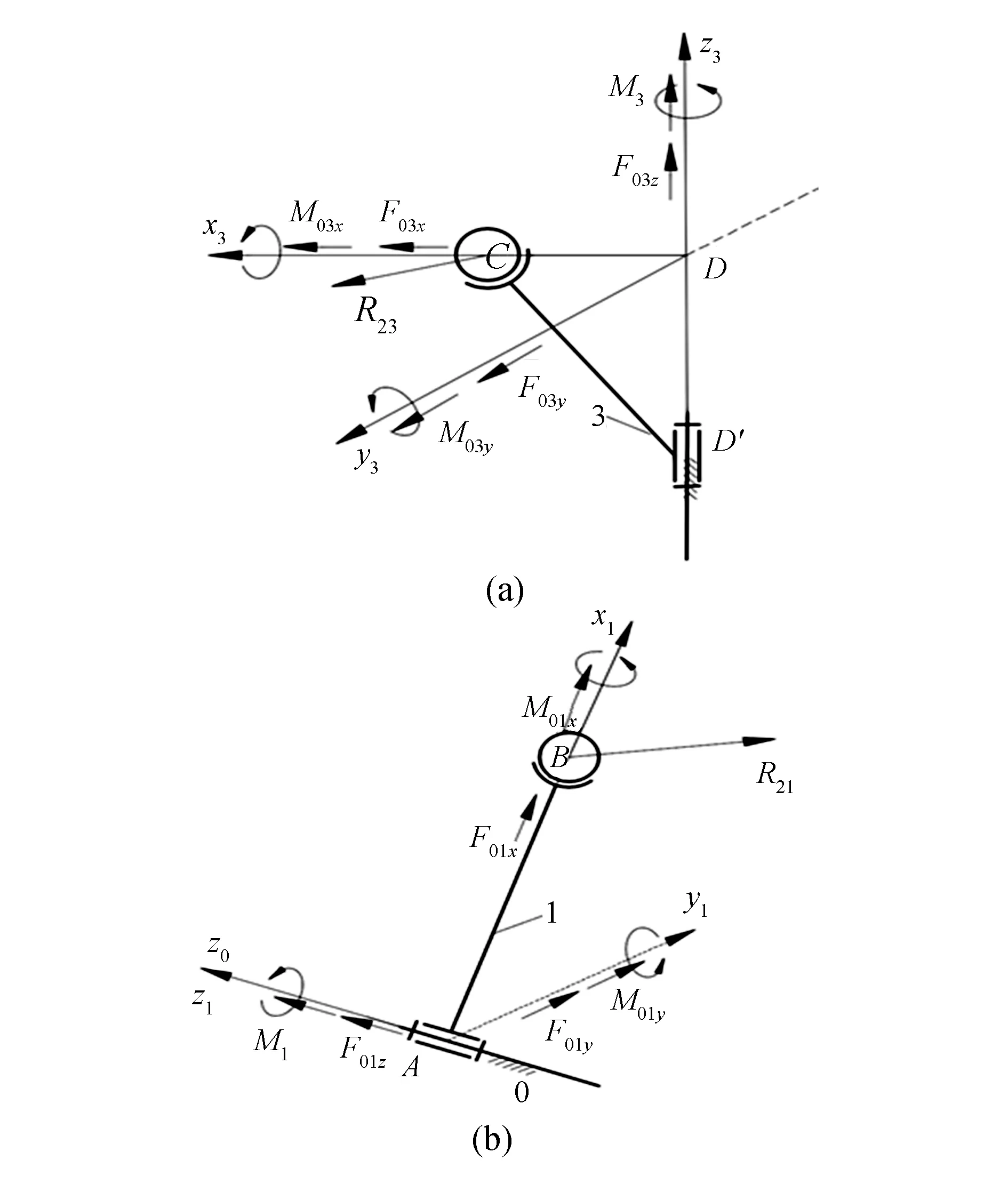
图3 RSSR受力示意图
(9)
式中:F03x,F03y,F03z,M03x,M03y为转动副D处约束反力在x,y,z轴向的分量;M3为转动副D处的水流对喷嘴的负载力矩。
联立式(6)~(9),可得:
(10)
以Ax1y1z1为参考坐标系,连杆2作用在曲柄1上的约束反力R21在x,y,z轴向的分量R21x,R21y,R21z为:
(11)
式中:(xB1,yB1,zB1)、(xC1,yC1,zC1)为B、C两点在Ax1y1z1坐标系下的坐标,其中xB1=h1,yB1=0,zB1=0。
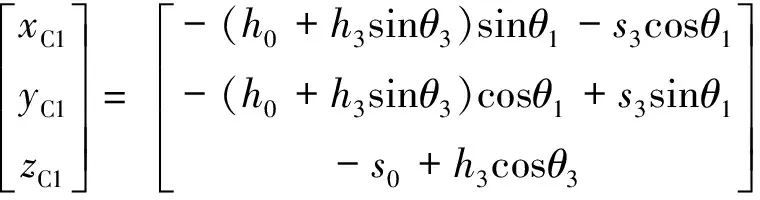
(12)
曲柄1的受力分析如图3(b)所示,根据曲柄1力平衡和力矩平衡关系,可得:
(13)
(14)
式中:F01x,F01y,F01z,M01x,M01y为转动副A处约束反力在x,y,z轴向的分量;M1为转动副A处的驱动力矩。
联立式(11)~(14),由R21=-R23解得:
M1=-h1R21y=
(15)
3 RSCS分析
3.1 RSCS运动分析
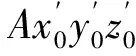
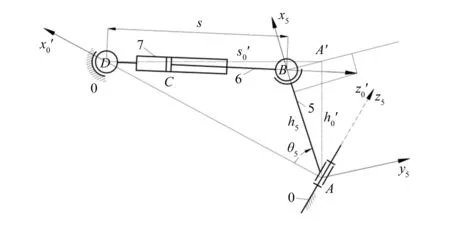
图4 RSCS简图
两球面副中心B、D之间的距离s为:
(16)
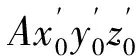
[xB,yB,zB]T=[h5cosθ5,h5sinθ5,0]T
(17)
(18)
式中:θ5为摇杆5的输出角。
将式(17)、(18)代入式(16)中,可得:
(19)
式中:s=x0+x,其中x0为活塞杆输出为0时两球面副之间的距离,x为活塞杆的位移。
3.2 RSCS静力分析
活塞杆为二力杆,约束反力的作用线沿杆中心线方向,大小待定。以Ax5y5z5为参考坐标系,活塞杆6作用在摇杆5上的约束反力R65在x,y,z轴向的分量R65x,R65y,R65z为:
(20)
式中:(xB5,yB5,zB5)、(xC5,yC5,zC5)分别为B、C两点在Ax5y5z5坐标系下的坐标。因为各构件在同一平面内运动,所以利用平面三角关系求得:
(21)
摇杆5的受力分析如图5所示,根据摇杆5力平衡和力矩平衡关系,可得:
(22)
(23)
式中:F05x,F05y,F05z,M05x,M05y为转动副A处约束反力在x,y,z轴向的分量;M5为转动副A处的负载力矩。
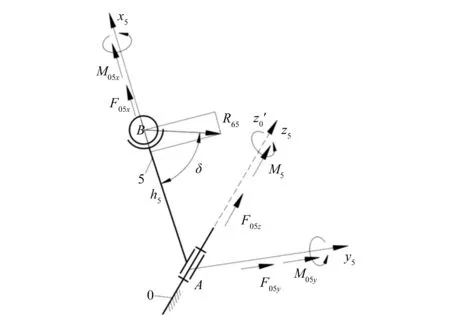
图5 RSCS构件5的受力示意图
联立式(20)~(23),解得活塞杆负载力FL为:
(24)
4 RSCS-RSSR组合转舵机构分析
4.1 组合转舵机构运动分析
如图6所示,转舵机构由RSCS和RSSR组合而成,传力杆4用来连接两个机构,并传递运动和力。
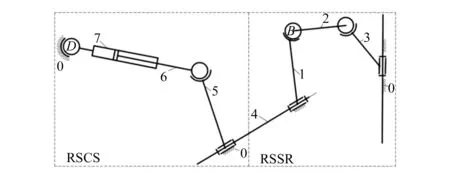
图6 转舵机构简图
在RSCS中,摇杆5的输出角θ5计算公式如下:
ΔθRSCS=θ5-θ5b(RSCS)
(25)
式中:θ5b(RSCS)为摇杆的基准角度,θ5b(RSCS)=61.687°;ΔθRSCS为摇杆转过的角度。
在RSSR中,曲柄1的输入角θ1计算公式如下:
θ1=θ1b(RSSR)+ΔθRSCS
(26)
式中:θ1b(RSSR)为曲柄的基准角度,θ1b(RSSR)=152°。
联立式(5)、(19)、(25)、(26)并消除中间变量,得到喷嘴转角随活塞杆位移的变化关系式:
(27)
图7为转舵机构的喷嘴转角与活塞杆位移关系曲线,可以看出液压缸活塞杆向x轴正向匀速运动时,喷嘴的转角由左满舵-30°向右满舵+30°变化,变化速率略有加快,但总体上该曲线接近于直线。
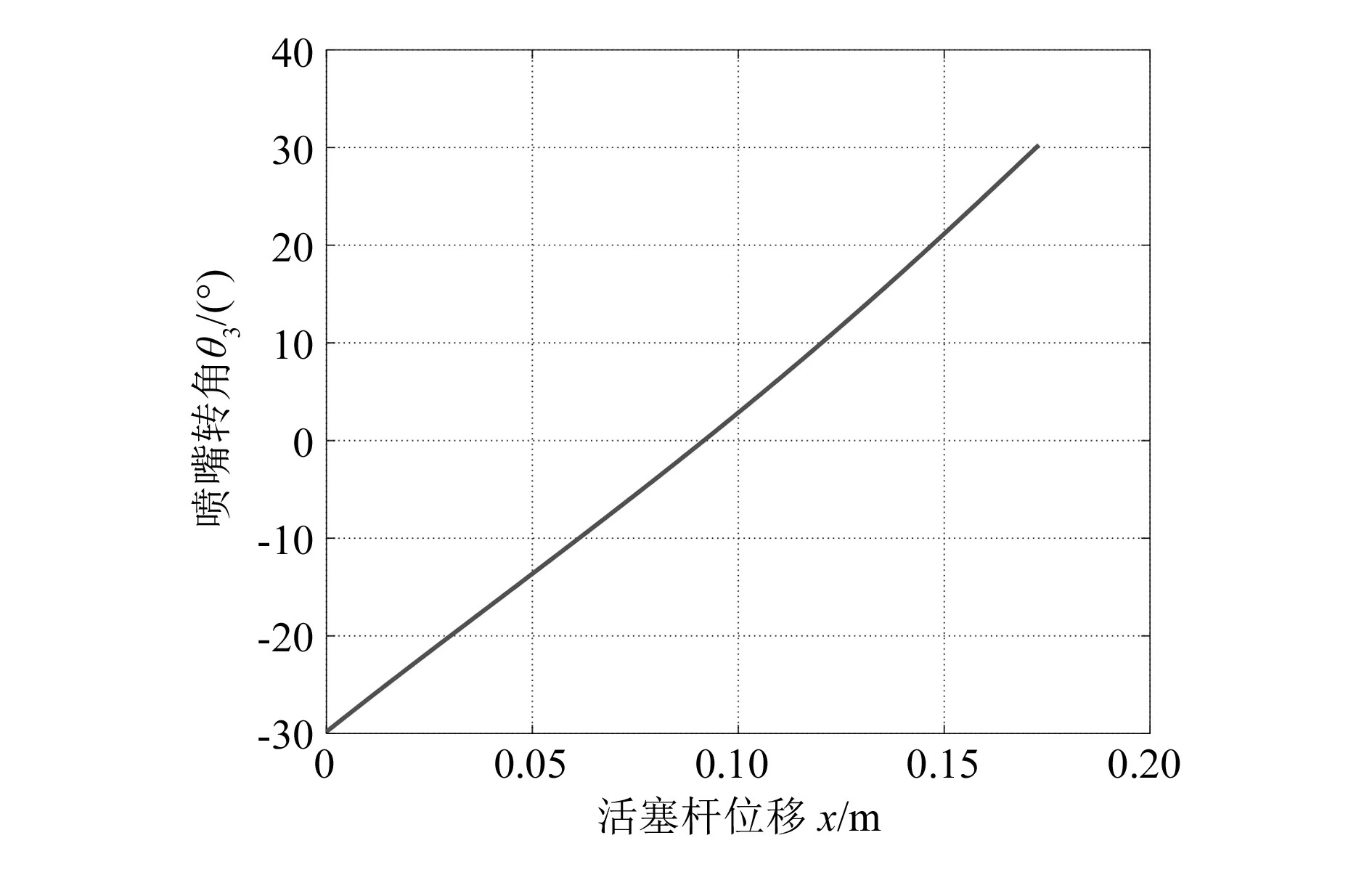
图7 喷嘴转角与活塞杆位移关系曲线
4.2 组合转舵机构静力分析
如图6所示,摇杆5和曲柄1固连在传力杆4上,摇杆与曲柄力矩平衡,联立式(15)、(24),得到活塞杆负载力FL与水流对喷嘴的负载力矩M3的关系式:
(28)
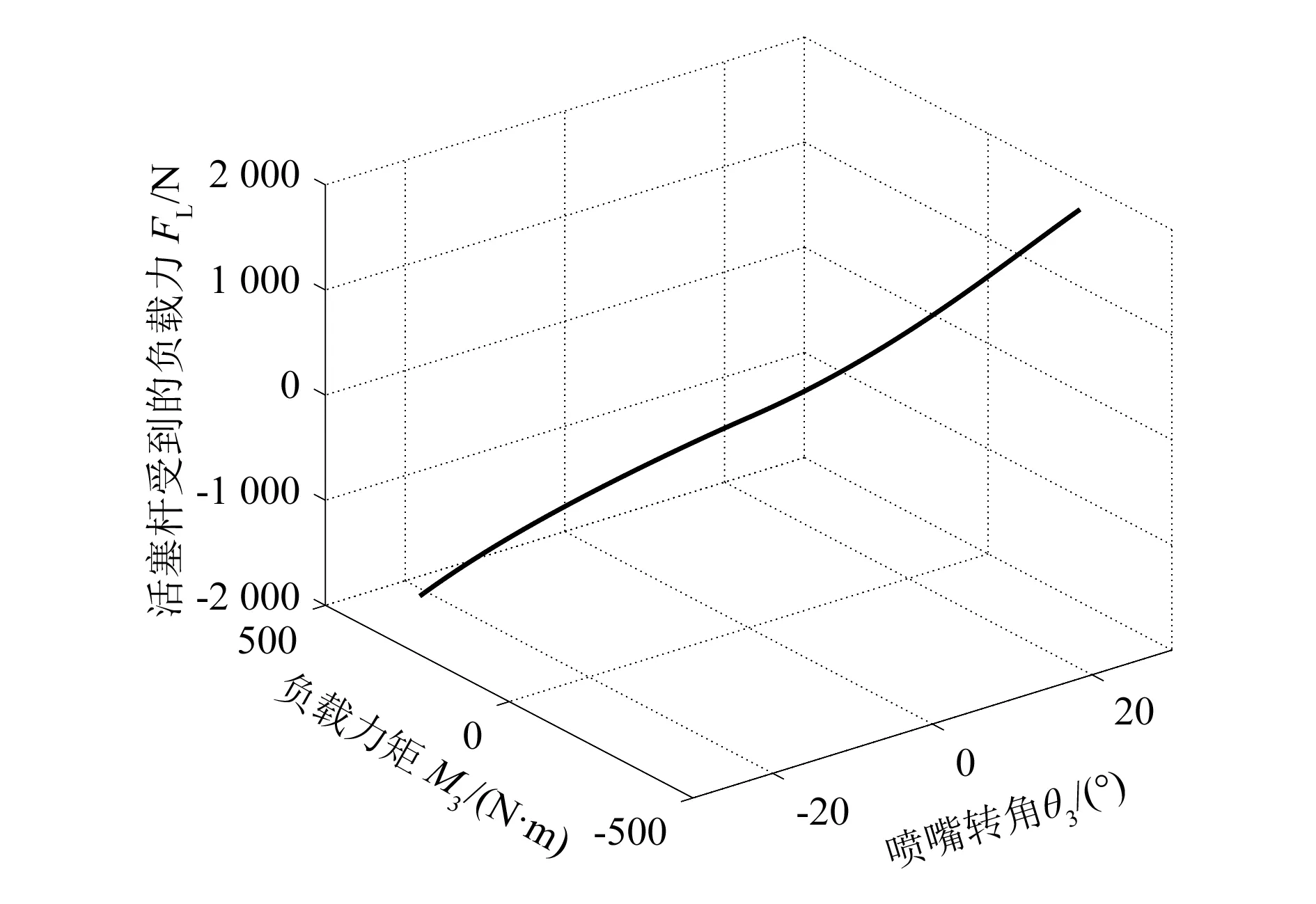
图8 活塞杆负载力与喷嘴转角、负载力矩关系曲线
结合式(28)和图8可以看出,活塞杆负载力同时与喷嘴的转角和负载力矩有关,且受力情况较好,几乎呈线性关系,均匀无突变。
5 结束语
本文采用解析法分别对RSSR和RSCS机构建立理论分析模型,以空间机构运动分析为基础,得到了RSSR曲柄输入角与喷嘴输出角的转角方程、RSCS活塞杆输入位移与摇杆输出角的位移方程。在运动分析的基础上,结合静力分析,得到机构中各运动副处的约束反力。通过机构组合,得到转舵机构的输入输出位移转角方程和静力平衡方程。通过绘制相关曲线可知,该转舵机构输入输出线性度较好,受力均匀,舵机的操纵性能优异。由于空间机构动力学的研究比较复杂,机构间的摩擦、间隙等因素还需在后面的工作中深入研究。

