BIM软件系统模型间智能联动机理探究

周宗泽张师定申俊昕

（1.上海同豪土木工程咨询有限公司，上海 200092；2.云南省交通规划设计研究院有限公司，云南昆明650041）

BIM软件系统由若干软件组成，无论各软件模型间，或是同一软件各模型间，常因专业功能要求其实现智能联动。智能联动是通过协调各子系统运作，使系统集成实现数据共享，便于统一分析处理，以实现子系统间的协同工作，使各子系统间完成智能联动，更大地发挥各子系统的作用，使多个子系统真正结合成为一个有机的大系统。

为清楚地研究系统智能联动机理，笔者撇开具体专业个性、抽取联动共性，建立了BIM软件系统智能联动的概念模型。

一、物理系统中的模型

软件系统是对物理世界的抽象刻画，是系统理论在数字技术中的体现。为了不失一般性，建议概念系统仅包括两个模型，或者两个子系统；进一步假设两个模型分别为长方体模型及球体模型（选择实体几何，便于直观理解）。

假设该物理系统的参考坐标系为空间直角坐标系，即系统坐标系O-XYZ，如图1所示。

该系统状态可用式（1）表达。

二、物理系统中的模型参数化

为了便于系统信息化及智能化，需依据专业知识，将该物理系统参数化，即系统所有模型参数化。

（一）长方体模型参数化

长方体模型参数化包括几何参数化与非几何参数化，结果如下。

1.长方体模型几何参数：L——长度（可变参数），与X轴平行；W——宽度（可变参数），与Y轴平行；H——高度（不变参数），与Z轴平行。

2.长方体模型位置参数：长方体的一个表面位于坐标面YOZ内，保持不变。

3.长方体模型自身几何约束：长方体各相邻表面相互垂直。

笔者建议将携带不变参数之长方体模型称为初始模型，即半成品模型。（注：对于长方体模型非几何参数，由于其不涉及几何联动，而且易处理，这里从略。）

长方体模型参数化结果可用式（2）表达。

1.2.2 培训标准 ①基本护理操作技能培训，按照上海市《护理临床教程》第2版的操作评分标准。②社区站点专科技能培训，统一按照第二军医大学出版社颁布的《社区公共卫生工作手册》所规定的工作内容。

（二）球体模型参数化

球体模型进行参数化包括几何参数化与非几何参数化。

1.球体模型几何参数：R——半径（可变参数）。

2.球体位置参数：（x0，y0，z0）——球心位置坐标，假定其在坐标系XOY面内（即z0=0），并且固定不动。

3.球体自身几何约束：球面任一点距球心之距离=该球体半径。（注：对于球体模型非几何参数，由于其不涉及几何联动且易处理，这里从略。）

球体模型参数化结果可用式（3）表达。

三、系统模型正向设计路线

深挖工程知识及BIM技术，笔者提出系统正向设计过程包括智能建模子过程与模型联动子过程，如图2所示。

智能建模子过程中，将设计过程分为标准设计与特殊设计；将设计构思过程模拟为“控制参数驱动经验规则库”之过程；巧妙地将经验规则库之“后件”关联到“标准模型库”或“模型参数库”，从而实现智能创建初始BIM模型。

模型联动子过程中，对于标准设计，采取人-机交互式修改BIM模型；对于特殊设计，采取功能性分析/检验及优化（局部优化）BIM过程，然后与关联模型进行联动优化。通过完成以上两个子过程，实现了正向设计，而输出结果——BIM模型即可满足交付标准。

四、模型间关联

系统的两个模型间发生的联系，包括几何方面的联系与非几何方面的联系，以便系统在满足功能要求的前提下实现系统最优。其中几何方面的联系（即模型装配）较为复杂。

不失一般性，假设该系统中两个模型间几何关联规则如下：无论系统参数数值作何变化，始终保持长方体与球体相切。（注：参数数值变化范围由领域专家来定，其最低要求是：保持几何体在概念上成立。）

由几何关联规则得到式（4）：

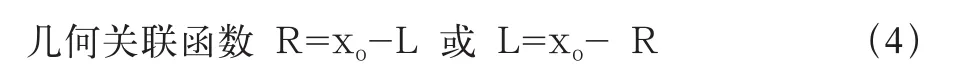
不失一般性，假设在该几何关联规则下，领域专家提出优化目标函数如式（5）所示，形成系统优化模型：

功能函数V长方体=L×W×H

V球体=4/3×π×R3

约束条件：见式（1）～（4）

几何关联函数：R=xo-L或L=xo-R

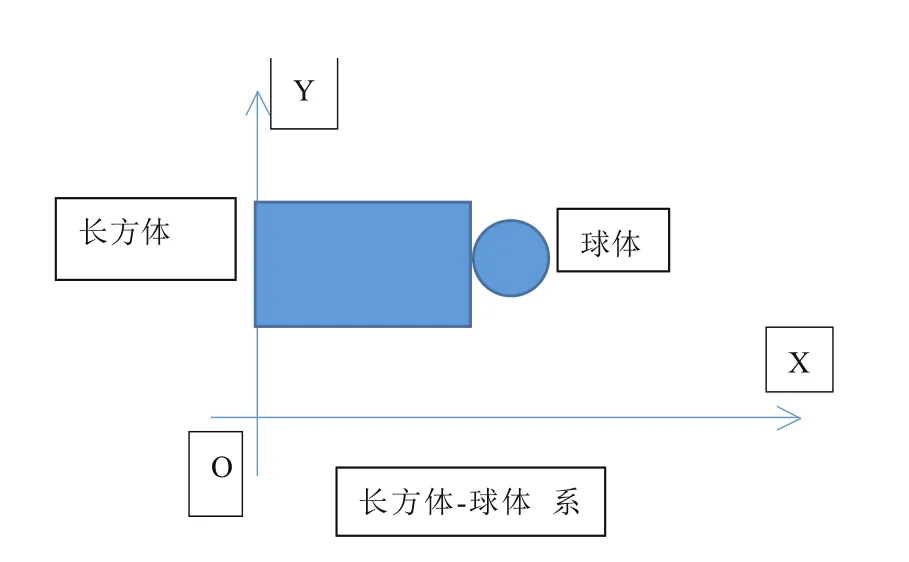
图1O-XYZ系统坐标系内长方体模型与球体模型智能联动之概念模型

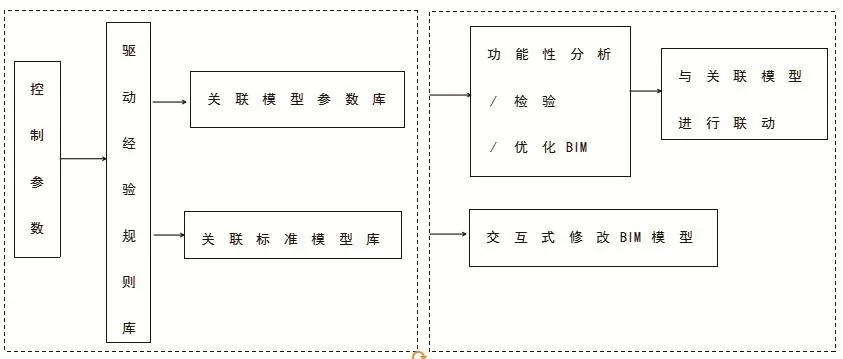
图2 系统模型正向设计技术路线

该参数化系统可由智能软件实现系统优化（子系统优化类同）。

五、参数化系统之联动

将系统模型参数化，并建立参数化系统，可实现改变一个可变参数数值，则其余参数自动（按规则）调整；当需要改变多个参数数值时，则依次改变，实现联动（互操作），从而生成一个新系统，即系统新状态。

六、BIM系统运作机理

综上分析，系统联动是系统最优化与动态适应性之表现。笔者提出BIM软件系统运作机理，以参数化模型描述专业实体，建立系统初始状态；依据优化准则，通过参数驱动模型，生成专业模型；基于参数化模型间智能规则，通过相关参数化模型间之联动，实现模型间协调，即系统整体最优。

为了进一步探索BIM技术，本文基于系统理论，用系统理论对BIM软件系统做了初步探索，并深度挖掘了BIM软件系统模型间智能联动机理。依赖BIM技术，系统理论发挥的作用越来越大。