等跨连续梁桥冲击系数的多参数分析

梁栋苏立超张硕邹轩

(1.河北工业大学，天津300401；2.河北省钢混组合桥梁技术创新中心，河北邢台054001；3.邢台路桥建设总公司，河北邢台054001）

目前，我国公路桥梁冲击系数的取值参照了《公路桥涵设计通用规范》（JTGD60-2015）中以桥梁基频为参数的一个分段函数式。但是除桥梁基频外，实际工程中的车辆冲击作用还与车速、车重等很多因素都有关。因此，基于车桥耦合振动详细讨论多因素耦合的冲击作用，是保证桥梁结构合理设计、安全运营的重要前提。

回顾近年来前人对冲击系数的研究，主要包括理论推导法、有限元模拟法和实验测量法三大类。在理论方面，桥梁工程结构动力学国家重点实验室徐文涛、张建波等人利用达朗贝尔原理得到了各振动方程，并分析了非平稳状态的车辆在桥梁行驶时的桥梁动力响应。在有限元方面，例如浙江大学建筑工程学院张鹤、张治成等人利用ANSYS软件开展的冲击系数研究，结果表明桥梁冲击系数与结构振动频率有关，提高车速并不意味振动冲击系数会增大。在试验方面，江西赣粤高速公路股份有限公司王德山、华东交通大学土木建筑学院桂水荣等人在利用汽车对某连续梁桥进行成桥动载试验中发现，冲击系数呈先增大后减小再增大的变化趋势。Kawatani、Komatsu S等人在两轴和三轴多自由度车辆对桥梁动力响应的研究中发现车轴数对冲击系数并无显著性影响。综上所述，在车桥耦合振动对冲击系数取值影响研究中，鲜有对多种因素耦合对常规连续梁桥冲击系数的影响研究，也鲜有对不同种类车辆和多车辆同时行驶时对冲击系数的影响研究。

本文结合ANSYS桥梁模型和UM车辆模型，对常规等跨连续梁桥的冲击系数开展多因素耦合分析。以两种不同的车辆模型，研究车速、车重、桥梁基频及其耦合对冲击系数的影响，为常规等跨连续梁桥的设计和运营安全提供技术支撑。

一、车桥仿真模型的建立

（一）模型建立

1.桥梁计算模型的建立

通过查阅《公路桥梁结构上部构造系列通用设计图》（2010年版）得知，常用等跨连续梁桥的跨径一般为20m、25m、30m、35m和40m，上部结构一般为横向4片装配式小箱梁或T梁。本文桥梁模型为小箱梁桥，桥梁信息如表1所示。

2.车辆模型

本文依据《中国汽车车型手册》《商用车辆和挂车制动系统技术要求和试验方法》及各车型出现的频率进行加权平均，选择了我国公路上行驶类型最多的两轴汽车和三轴货车进行分析，车辆参数如表2所示。

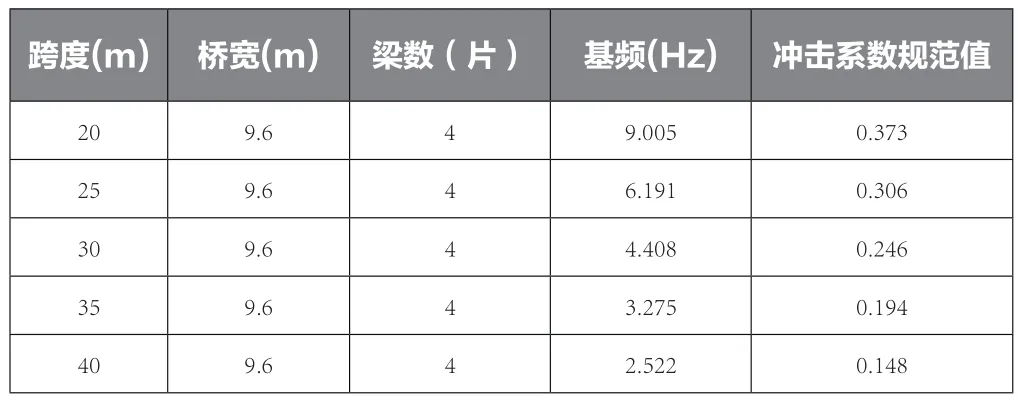
表1 桥梁信息

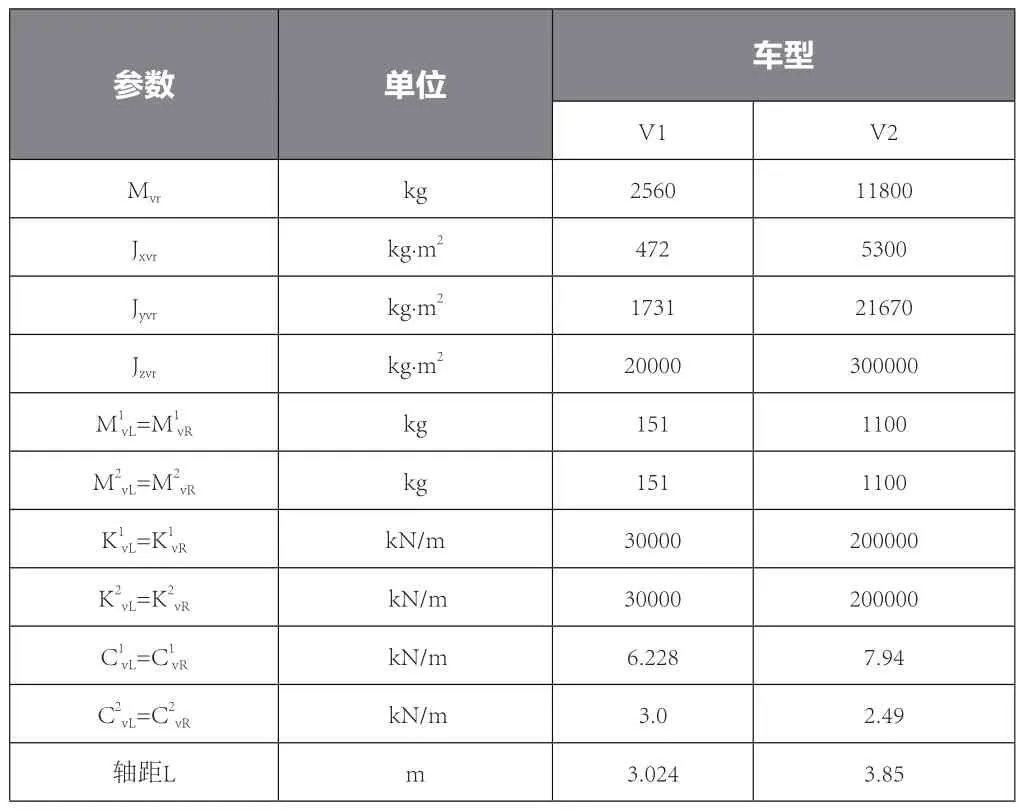
表2 车辆参数

表中，Mvr—车体的质量，下标vr表示车辆刚体；分别表示第i个轴处左右车轮的质量；Jxvr、Jyvr、Jzvr分别表示车体的侧翻、点头和摇头转动惯量；分别表示第i个轴处左右车轮的竖向刚度；分别表示第i个轴处左右车轮的竖向阻尼。

3.车桥耦合计算模型

利用UM软件Input前处理系统连接桥梁节点与桥墩，约束连续梁桥在各桥墩位置的横向、竖向和纵向自由度。耦合车辆模型与桥梁模型，使二者成为一个动力耦合系统。

（二）车桥耦合分析的实桥验证

为了验证上述联合仿真模型的正确性，现选择天津市内某3×34m的等跨连续梁桥进行实桥验证。该桥混凝土强度为C50。试验车辆的车重为Mvr=35000kg，分别使两辆货车按照60km/h和80km/h的均速进行跑车试验，获取桥梁中跨跨中截面的动位移响应。对比两种时速下的试验动位移数据和UM模拟位移数据发现，60km/h时的最大误差值为5%，80km/h时的最大误差值为3%，证实了本文所建立车桥耦合振动仿真分析模拟的可靠性。

（三）等跨连续梁桥冲击系数的车桥耦合分析

1.计算工况

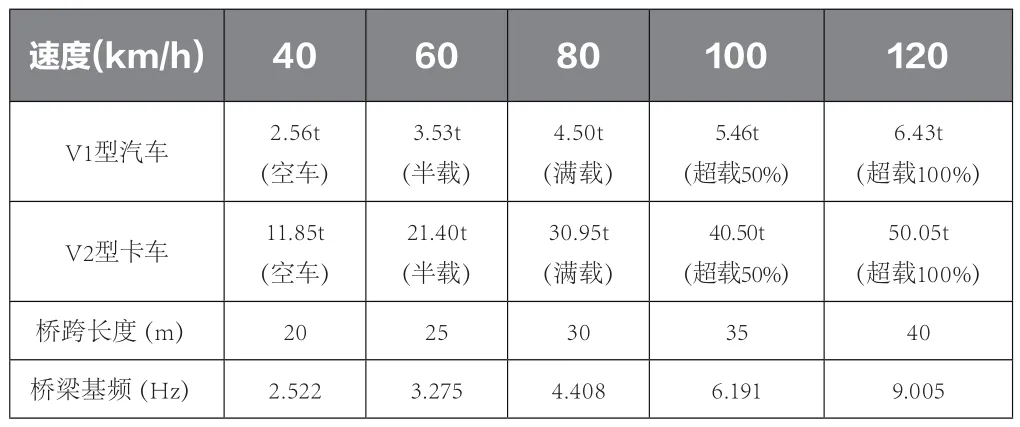
表3 计算工况

为研究车桥耦合振动对冲击系数的影响，将各因素工况汇总如表3所示。根据国标GB1589-2016和超限运输车辆行驶公路管理规定，本文将2轴车满载重量设置为4.50t，3轴车满载重量设置为30.95t。

分别以车速、车体总重、桥梁基频为自变量参数，模拟在改变V1和V2单辆车的车辆载重、两辆车在两个车道上并排行驶的条件下，分别让同类车型的一辆车和两辆车首先以5种不同时速在连续梁桥行驶；其次在5种不同桥跨长度的连续梁桥行驶；最后在5种不同桥梁基频的连续梁桥行驶。

2.计算结果

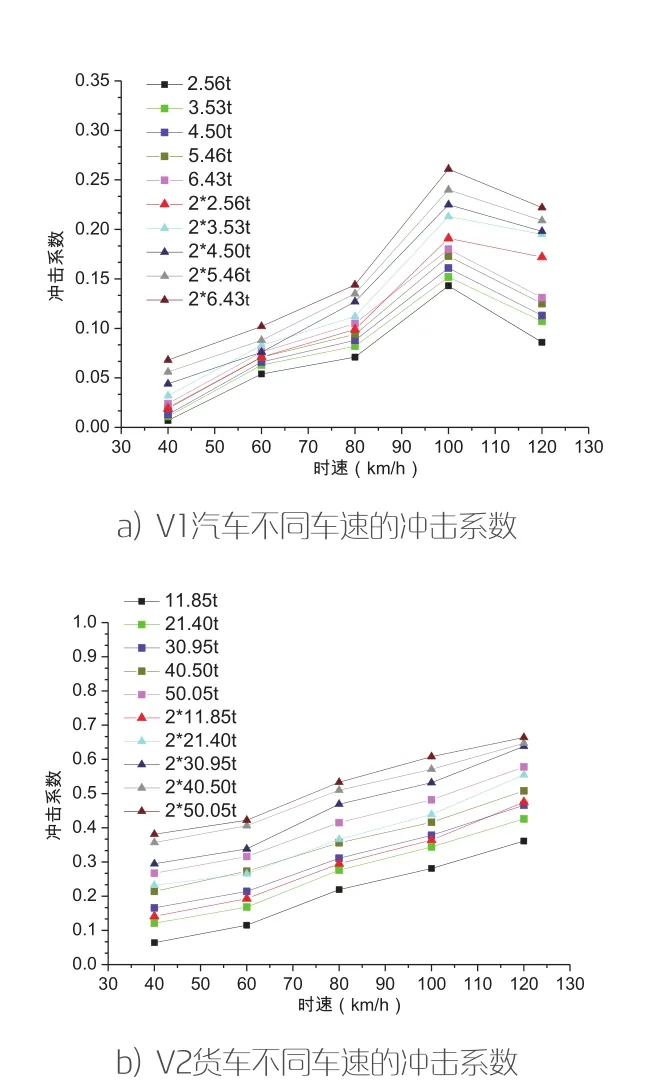
图1 不同时速下的桥梁冲击系数曲线

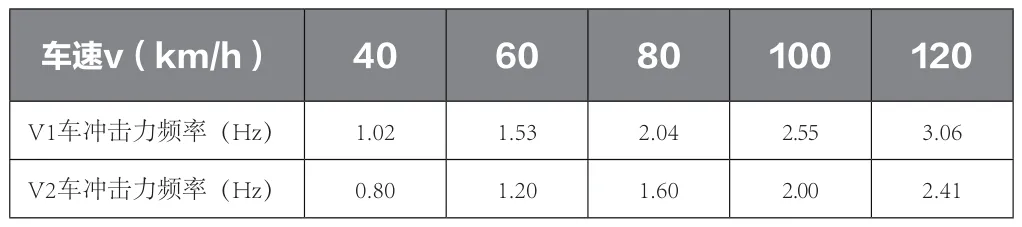
表4 不同车速下冲击力频率

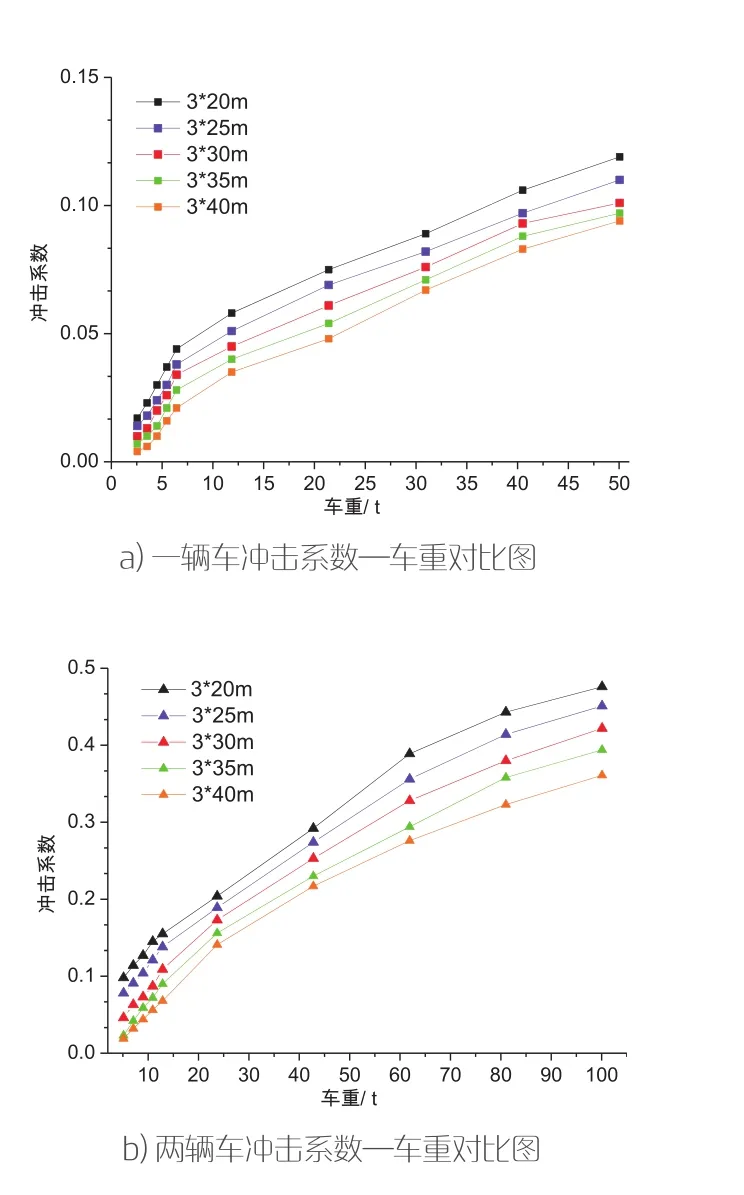
图2 不同车重下的冲击系数曲线

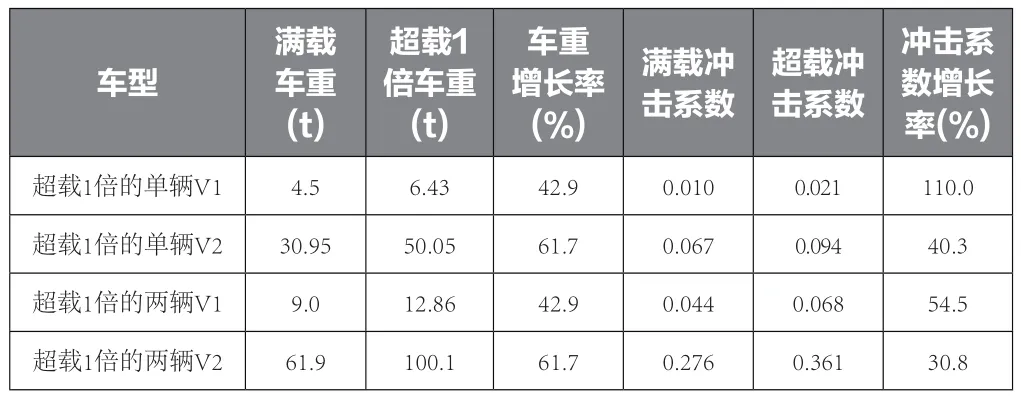
表5 不同车重下冲击系数增长率

车速对冲击系数的影响。选取3×40m的桥梁，按工况1行驶，得到不同时速下冲击系数与车速的关系。由图1可知，无论是一辆车还是两辆车行驶时，冲击系数基本都在增大，只有V1车在100km/h～120km/h时冲击系数有所减小。

由于不同行驶速度产生的冲击力频率不相同，当冲击力频率和桥梁基频越近时，车桥共振越剧烈，冲击系数也越大，冲击力的频率计算公式(1)：

其中fv表示冲击力频率（Hz），v表示车速（m/s），L表示车辆轴距（m）。根据式（1）可得不同时速下的冲击力频率如表4所示。

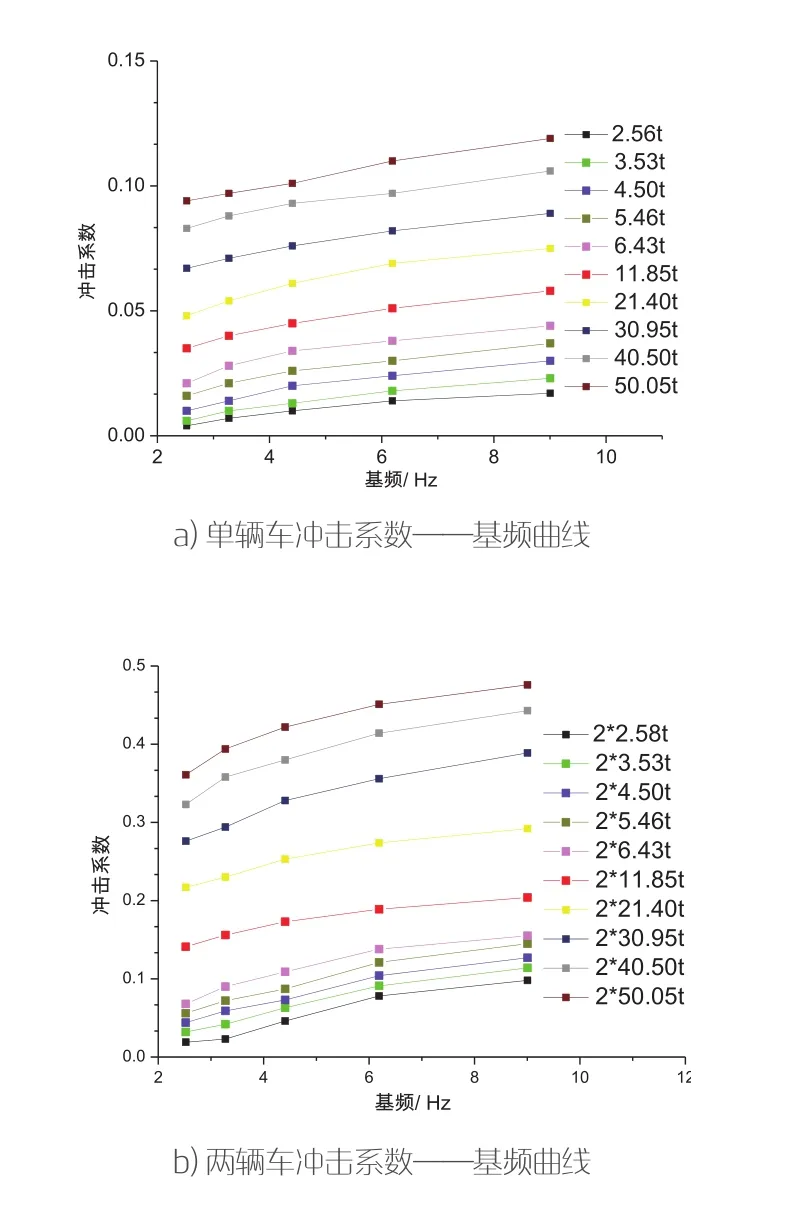
图3 不同桥梁基频下的冲击系数

由表4可知，V1车、V2车的冲击力频率在分别在车速为100km/h、120km/h时与桥梁基频最接近，因此根据共振原理V1车、V2车在时速为100km/h、120km/h时冲击系数最大。

车重对冲击系数的影响。在不同桥跨下，冲击系数与两种车型的车重的关系，如图2所示。以桥跨为3×40m的桥梁为例，车辆超载情况与冲击系数增长的关系如表5所示。观察图表可知，当桥跨长度一定时，冲击系数随着车重的增加而增大。当车辆的悬挂系统受到的车辆重力越大，车辆竖向颠簸使压缩长度恢复越多，竖向对桥梁的反向冲击力更大。

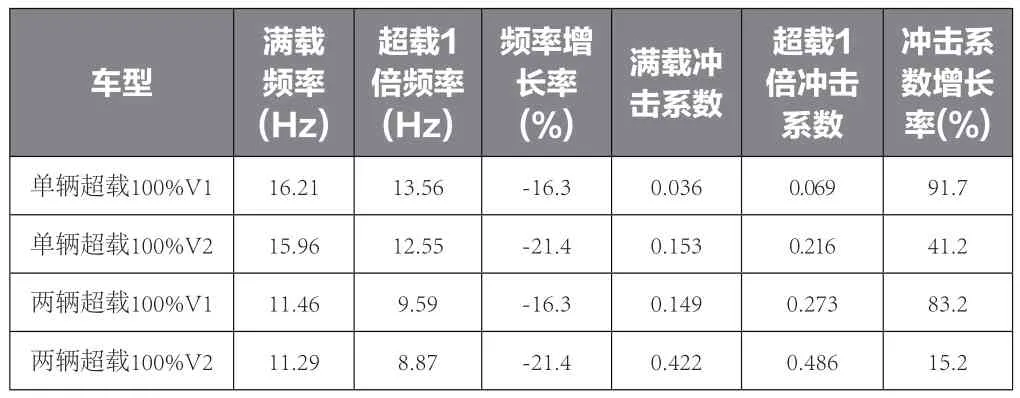
表6 不同基频下冲击系数增长率

桥梁基频对冲击系数的影响。选取V1车和V2车在满载和超载100%时，冲击系数随桥梁基频2.522Hz增大到9.005Hz时的变化进行桥梁基频因素的影响分析，如图3所示。

如图3所示，各工况下冲击系数都随桥梁基频的增加而增大。当桥梁基频与车辆整体的固有频率越相近时，车桥共使车辆对桥梁的竖向冲击力越大。假设车辆为单自由度弹性质体，则固有频率可按式(2)计算，结果如表6所示。

由表6可知，无论是V1车还是V2车，两辆车的固有频率都更加接近于桥梁基频最大值9.005Hz，由于每辆车对桥梁的共振作用会产生相互之间的叠加效应，因此两辆车的冲击系数要大于一辆车的冲击系数。

三、多因素耦合分析

（一）公式拟合

为得出多因素下的冲击系数公式，本文拟先得出车速、总车重、桥梁基频各自的冲击系数拟合公式，然后根据车速—车重、车重—基频之间的影响权重，将三种影响因素各自加权，最后得到考虑多种因素下的冲击系数拟合公式。

同一车速的拟合公式为：

式中，v表示车速（km/h）。对回归方程进行显著性检验，获得表7显著性检验信息。

令显著性水平α = 0.05，由表7可知P＜α，故相关性显著。拟合车速与车重相对影响公式：

式中，m表示总车重（t）检验式（4）的相关性，P＜α，相关性显著。得到车速和车重的冲击系数相对权重之比为0.38：1。

依照式（3）的拟合方法，得到车重的拟合公式：

式中，m表示车重（t）同时拟合出同一桥梁基频的拟合公式为：

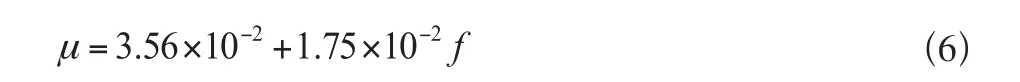
式中，f表示桥梁基频（Hz）由于（5）式的不同桥跨长度和（6）式中的桥梁基频对应，可直接得到车重m和桥梁基频f的冲击系数相对权重之比为1：3.95，车速、车重、桥梁基频的权重系数依次为0.07、0.19、0.74。将车速、车重、桥梁基频的拟合公式各自乘以权重系数后，得到多因素下的拟合公式为：

式中，v表示车速（km/h），m表示车重（t），f表示桥梁基频（Hz）。

（二）对比分析

在《公路桥涵设计通用规范》（JTGD60-2015）中，桥梁冲击系数µ是桥梁基频f的分段函数。因此本节将桥梁基频作为自变量，对冲击系数的规范值和拟合值进行对比分析。V1的单辆和双辆车的拟合冲击系数值和模拟值均小于规范值。这说明当桥梁基频大于2.522Hz时，现行规范对V1车是可以使用的。对于V2车，在2.522Hz时两辆车的模拟值大于规范计算值。这说明现行规范对车体超重的非单辆V2货车并不适用。拟合值和模拟值之间最大误差不超过15%，具有一定可靠性。

三、结语

车速对冲击系数变化有影响，不同车型达到最大冲击系数的车速不尽相同。冲击系数随着车重增大而增大，两辆车并排行驶时的桥梁冲击系数要大于单辆车行驶时的2倍。桥梁基频变化时，其越接近车辆固有频率，冲击系数越大。

责任编辑/ 孙誉菡 美术编辑/ 王德本