基于改进LeNet-5 的形状类似物体识别方法*
郑 睿 ,余 童 ,程 龙 阅
(1.安徽师范大学 物理与电子信息学院,安徽 芜湖241002;2.安徽省智能机器人信息融合与控制工程实验室,安徽 芜湖241000)
0 引言
当前,基于视觉的智能机器人已经应用于各领域中[1]。 当机器人面临需要抓取形状类似、硬度不同的物体时,智能机器人应选择不同的抓取力。 因此, 通过视觉识别出这类物体具有较高实用价值。利用深度学习[2-3]对图像进行识别是较为高效的方法,国内外相关研究已经在车辆及车道线检测[4-5]、人脸识别[6-7]、手写体识别等领域取得较多的成果。
近年来,针对形状类似物体的识别也取得了一定的成果。 张雪芹等人[8]利用深度学习AlexNet 网络实现了对多种类植物图片进行分类识别。林思思等提出融合深度特征和人工特征的花卉图像特征提取方法, 并在此基础上实现花卉图像的分类[9]。西南交通大学秦放[10]提出基于深度学习的昆虫图像识别研究,扩充了昆虫样本集,基于昆虫图像识别的任务需求和样本集,从网络和训练两个方面进行改进。 张立超等人利用LeNet-5 网络对两种品种的苹果进行分类识别[11],在两种苹果的分类中取得不错的效果。 但大型的神经网络一般通过加深网络深度获得高精度的识别率,其结构较为复杂,运算量大,无法满足快速识别的要求。
因此,本文选择LeNet-5 网络作为研究对象,由于LeNet-5 网络结构较为简单,运算量较小,对硬件配置要求低,能够在满足网络轻量化的前提下对形状类似、硬度不同的物体实现快速识别。 传统LeNet-5 网络在识别精度上尚有不足。 为了能够提高识别精度且尽可能地减少运算量,本文将传统卷积核拆分为非对称卷积核以缩短计算时间;在网络中间加入BN 层[12]使中间层的数据输出更加稳定,提高网络的训练精度;采用全局平均池的方法取代原模型Flatten 层以降低运算量[13]。 通过这三种方式有效地改进了LeNet-5 网络,使其能够适用于移动机器人平台,实现对物体的识别。
1 LeNet-5 改进网络的构建
LeNet-5 网络是传统卷积神经网络的代表,最早由LECUN Y[14]提出,其结构如图1 所示。 该网络共有7 层,分别为卷积层、池化层、卷积层、池化层、全连接层、全连接层、输出层。
LeNet-5 网络是传统针对字符识别的网络,该网络结构简单,易于运算,它在对形状差异较大的图像进行识别时,能取得良好的识别效果。 但对于形状类似、硬度不同的物体进行识别时,尚不能取得良好的分类识别效果。
1.1 双层非对称卷积神经网络的构建
传统LeNet-5 网络使用单层较大的卷积核,较大卷积核在计算上会增大运算量,耗时时间较长。由于双层非对称卷积比单独使用一个较大的卷积核拥有更少量的参数,且能够加快计算,使得网络深度变深,同时,双层非对称卷积会比单层大卷积拥有更多的非线性变换,使得网络较原网络有更强的特征提取能力,因此本文构建双层非对称卷积对图片进行运算,运算原理如图2 所示。

图2 双层非对称卷积原理图
图2 中,假设输入图像的维度为5×5,则x11…x55代表输入图像中的像素值,将传统3×3 的卷积核拆分为卷积核1(维度为3×1)和卷积核2(维度为1×3)两个卷积核,这两种卷积核为非对称卷积核。 首先利用卷积核1 对输入图像进行卷积操作,遍历输入图像后可得到维度为3×5 的特征图1,特征图1 的数值分别为y11…y35,计算公式为:
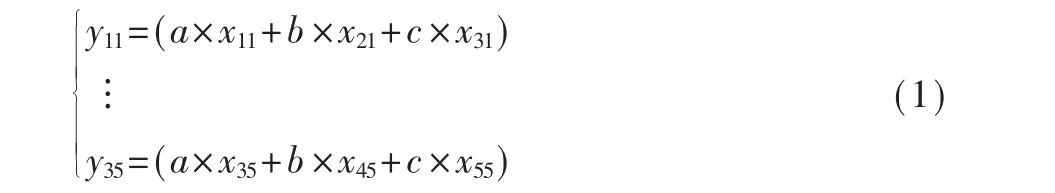
其中,a、b、c 代表卷积核1 中的数值。
经过卷积核1 进行卷积后得到特征图1,维度为3×5,再用大小为1×3 的卷积核2 对特征图1 进行卷积操作,遍历特征图1 后得到尺寸为3×3 的特征图2,特征图2 内数值分别为z11…z33,计算公式为:

图1 LeNet-5 网络结构图

其中,d,e,f 代表卷积核2 中的数值。
以3×1,1×3 的非对称卷积核对维度为5×5 的输入图像进行卷积运算为例:由双层非对称卷积原理图及式(1)、式(2)可以推出,共需要72 次运算可得到特征图2。 而如使用传统3×3 卷积核进行卷积,需81 次运算才可得到特征图2。 一般来说,输入图像越大,卷积次数越多,双层非对称卷积运算减少的参数量越大。 双层非对称卷积核不但能够加深网络深度,而且在双层的前提下依然比单层卷积核的计算量小,有效降低了参数量。 通过这种方式一方面可以减小参数量,减轻过拟合,另一方面可以增强模型的表达能力,使得非对称卷积取得的效果比对称卷积核更好,增加特征多样性。
1.2 批量归一化
传统LeNet-5 网络中,并未对网络中间层的数据进行处理,这样使得中间层的数据较为离散,不利于网络训练。 为了能够对数据进行标准化处理,使得网络中间层的数据稳定,在网络中每层卷积层后加入批量归一化方法,在模型训练时,批量归一化利用小批量数据的均值和标准差,不断调节卷积层后的输出,使得输出数据更加稳定。
以图2 为例,卷积层输出为特征图2,设其输出为Z={z1,…,zn},那么其均值μZ为:

式(3)中zi表示Z 中第i 个数据。进一步可得Z 的方差DZ为:

在此基础上对Z 进行归一化,使变换为Zˆ。 Zˆ中的 第i 个 数 据为:

式(5)中,ε 表示一个微小的常数,为了使得归一化后的数据仍能保持原有的分布特征,采用学习型的参数γ 和β 对Zˆ进行批量归一化处理,使Zˆ变换为Z~。中的第i 个数据为

式(6)中,γ 和β 将和其他的权重参数等一起用梯度方法进行训练,其最终的值将使损失函数达到最小值。
1.3 全局平均池化
传统LeNet-5 网络中一直用Flatten 全连接输入到softmax 中对其做分类,但是全连接存在参数量过大、训练速度低及容易过拟合等问题。 为了达到减少参数、缩减训练时长的目的,本文用全局平均池化(Global Average Pooling,GAP)的方式替代Flatten层。 全局平均池化示意如图3 所示。

图3 全局平均池化层示意图
LeNet-5 中采用全连接方法把卷积输出的二维特征图转换为一维向量,对此向量做乘法,最终降低其维度,然后输入至softmax 层中对其做分类。 由于在全连接层中的每一个节点都与上一层的每一个节点连接,这就会导致参数量过大,容易过拟合。采用全局平均池化法代替全连接层,对每个特征图整张图片进行平均池化,这样每张特征图只得到一个输出,可以大大减少网络参数。此外,每张特征图就相当于一个输出特征,这个特征即输出类别的特征。 通过全局平均池化的方法对每一张特征图进行运算,无需单独对参数进行优化,这样会大大减少参数量,减轻过拟合现象。
2 数据集的增广方法
上述内容通过改进卷积层、添加BN 层、采用全局平均池化等方式完成了对LeNet-5 网络的改进,为了进一步增强网络的训练效果与识别能力,需要对网络输入大量数据来提高网络的识别精度。 因此,在采集了部分数据集的基础上,对原数据集进行增广,利用视角变化几何原理对图像进行变换。
在视角变化几何原理中,图像上某点像素可以用坐标(x0,y0)表示,假设对图像进行平移变换,经过平移量(Δx,Δy)后,像素点坐标变为(x1,y1),则平移操作的矩阵表达式为:
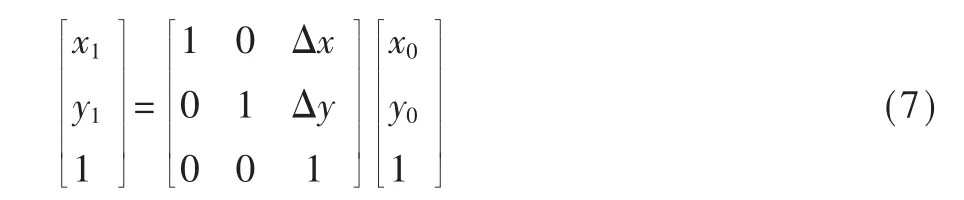
假设对图像进行水平镜像变换,该像素点坐标变为(x0,w-y0),则水平镜像变换的矩阵表达式为:

垂直镜像变换参照水平镜像变换。
假设对图像进行旋转变换,该像素点的坐标变为(x1,y1),一般旋转中心为图像的中心,顺时针旋转角度为θ,则旋转变换的矩阵表达式为:

假设对图像进行成比例缩放后,该像素点坐标变为(x1,y1),kx表示图像横向缩放比例,ky表示图像纵向缩放比例,则成比例缩放后的矩阵表达式为:
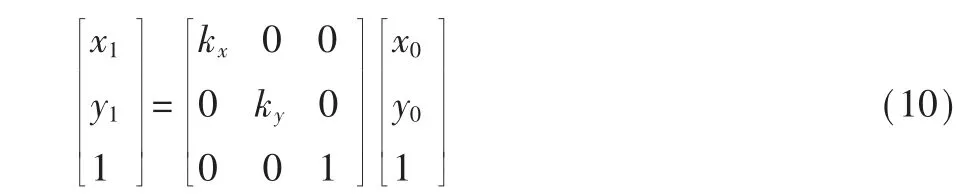
根据式(7)~式(10)对图像进行平移、镜像变换、旋转、缩放等增广变换,大大增加了数据集的容量。其中图像水平平移中的Δx、竖直平移中的Δy 均取值为0.2,图像旋转的角度θ 取值为30,图片缩小幅度kx、ky值为0.8。
3 实验结果与分析
基于上述方法,对鸡蛋、苹果、芒果、石块四种常见的形状类似、硬度不同的物体开展识别实验,验证方法的有效性。
3.1 实验参数
3.1.1 相关环境配置
实验中硬件配置:Intel®CoreTMi3-3110M CPU@2.40 GHz 处 理 器、NVIDIA GeFORCE GT 630 MB 显卡、8 GB 内 存。
实验软件环境:主机操作系统为Windows7/64 位操作系统;虚拟机操作系统为Ubuntu/64 位操作系统;深度学习框架为TensorFlow/Keras; 环境管理器为Conda4.7.10;编程环境为Python 3.7.3。
3.1.2 网络参数
LeNet-5 网络参数和改进型的网络参数分别如表1 与表2 所示。
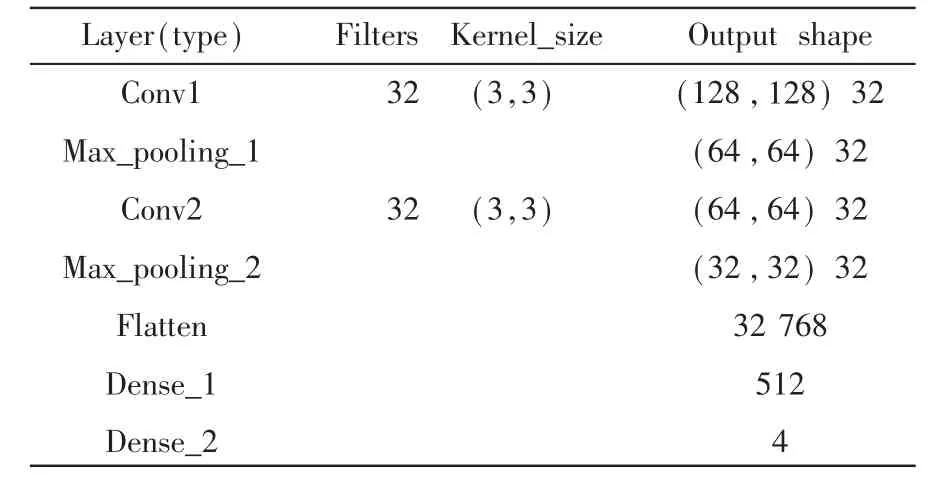
表1 原网络结构参数

表2 LeNet-5 改进网络结构参数
表1 中参数为LeNet-5 网络进行实验得到的结构参数。 卷积核数量为32,大小为(3,3),对输入大小为(128,128)图像经Conv1 进行卷积操作,经过激活函数tanh 运算再进行最大池化操作,经过Maxpooling1 得到数量为32,大小为(64,64)的特征图。 再经过Conv2 卷积层、 激活函数运算与最大池化层Maxpooling2 后得到数量为32,大小为(32,32)的特征图。 Flatten 层得到输出结果参数为32 768, 后两层全连接层对特征图进行分类得到输出结果为4。
表2 中参数为LeNet-5 改进型网络实验得到的结构参数。输入图像大小为(128,128),经过Conv1_1层大小为(3,3)的卷积核与Conv1_2 层大小分别为(3,1)(1,3)的卷积核进行卷积运算后得到大小为(128,128)的32 个特征图。“padding=same”操作保证边缘信息被充分提取。 此处采用的激活函数为ReLU函数且之后的每次卷积后都选择ReLU 作为激活函数进行运算。 为了使神经网络训练过程中每一层输入保持相同分布,在部分卷积层后对其进行BN操作。 接着对其进行最大池化, 经过最大池化层MaxPooling_1 后,得到的特征图大小为(64,64),且数量保持不变。 再对其进行单卷积层Conv2 的卷积运算,得到输出数量为32,大小为(64,64)的特征图。卷积层Conv3、Conv4 与最大池化层MaxPooling_2 计算原理与上述相同, 经过Conv4_1、MaxPooling_4 后得到数量为64,大小为(8,8)的特征图,改进的网络用全局平均池化代替了原来的Flatten 层。最后两层全连接层,根据特征组合进行分类,本实验是对四种目标图片进行分类,经最后一层全连接层得到输出为4。
3.2 原始图像的采集和数据增广
实验使用生活中较为常见的鸡蛋、 芒果、石块、苹果四种形状相似物体的图片。 采用实物拍摄的方法获得每种物体的60 张实物图, 并随机取3张图片。 实物图如图4 所示。
根据增广的参数设置,对四种物体的原始图像进行增广,使得原始的一幅图像增广为7 幅。 对图4中每种物体的第一幅图进行增广,图像增广后的结果如图5 所示。
3.3 特征图的提取与分析
通过增广方法得到较多的样本集。 在对样本集的训练过程中,得到输入图像的特征图,再对特征图进行提取。 以一张苹果的样本图为例,得到的特征图如图6 所示。
图6(a)是利用32 个卷积核对输入图像进行卷积操作得到的特征图,每张小特征图分别是32 个卷积核中的一个卷积核对输入图像进行特征提取所得到的。 图(b)是在输入图经过卷积后再对其进行最大池化得到的特征图,包含32 幅小特征图。 图(c)为利用64 个卷积核继续对输入该层的图进行卷积,图(c)中部分特征图显示黑色,说明其未学习到上一层输入图像的特征,意味着需要更多的数据和训练对其进行改善,使网络尽可能地学习到输入图像的细节特征。 图(d)是提取出的最终特征图,较图(a)、(b)、(c)来说,图(d)中包含的特征图更加模糊,色彩变化较大,说明随着网络深度的增加,提取出了更高级的特征。
3.4 网络的训练
根据设置的参数,得到未改进的LeNet-5 网络与改进后的网络,两种网络训练精度值与损失函数值变化曲线如图7、图8 所示。 图中实线曲线代表训练精度,虚线曲线代表损失值曲线,横坐标为迭代次数,纵坐标为数值。
图7 中,原始LeNet-5 网络在迭代区间0~40 内,训练精度明显上升,在迭代次数为50 时,训练精度达到0.8。 在迭代区间40 ~80 内,训练精度略有上升。 在迭代80 次之后,训练精度值基本保持平稳,精度值在0.85 左右浮动。 损失值在区间0~80 内下降较明显, 在80~150 区间内逐渐稳定在0.3 左右浮动。 图8 中,LeNet-5 改进后网络在迭代区间0~20内,训练精度明显上升,在第20 次时训练精度约达到0.78。 在 迭 代 区 间20 ~70 内, 训 练 精 度 略 有 上升。 在迭代70 次之后,训练精度值基本保持平稳,精度值在0.90 上下浮动。 损失值在0~80 次内逐渐下降,在80 次后逐渐在0.24 上下浮动。

图4 四种物体的原始图像

图5 图像增广示例图

图6 部分特征图

图7 LeNet-5 网络的训练精度与损失函数曲线图
为了能更加精确地分析训练精度与损失值,以10 次迭代为一个区间,得到具体数值如表3 所示。
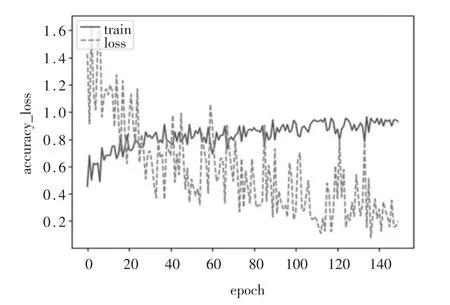
图8 改进LeNet-5 网络的训练精度与损失函数曲线图
由表3 可看出,改进后的网络训练精度在各个迭代区间内均高于未改进网络的精度,在迭代次数为80 次时网络完成收敛,在80 次后再进行迭代网络整体训练精度变化不大。 网络在迭代区间为140 ~150 内训练精度达到0.914,比原网络训练精度高0.08。 两种网络损失值在迭代50 次前差别不大,在80 次后改进网络的损失值低于原网络。 在120 次后网络损失值稳定在0.28 左右,低于原网络的0.34。
3.5 网络识别精度的验证
对于需要识别的四种物体,各取50 张图片作为测试样本,这些测试样本均未用于训练网络,所得到的结果如表4 所示。
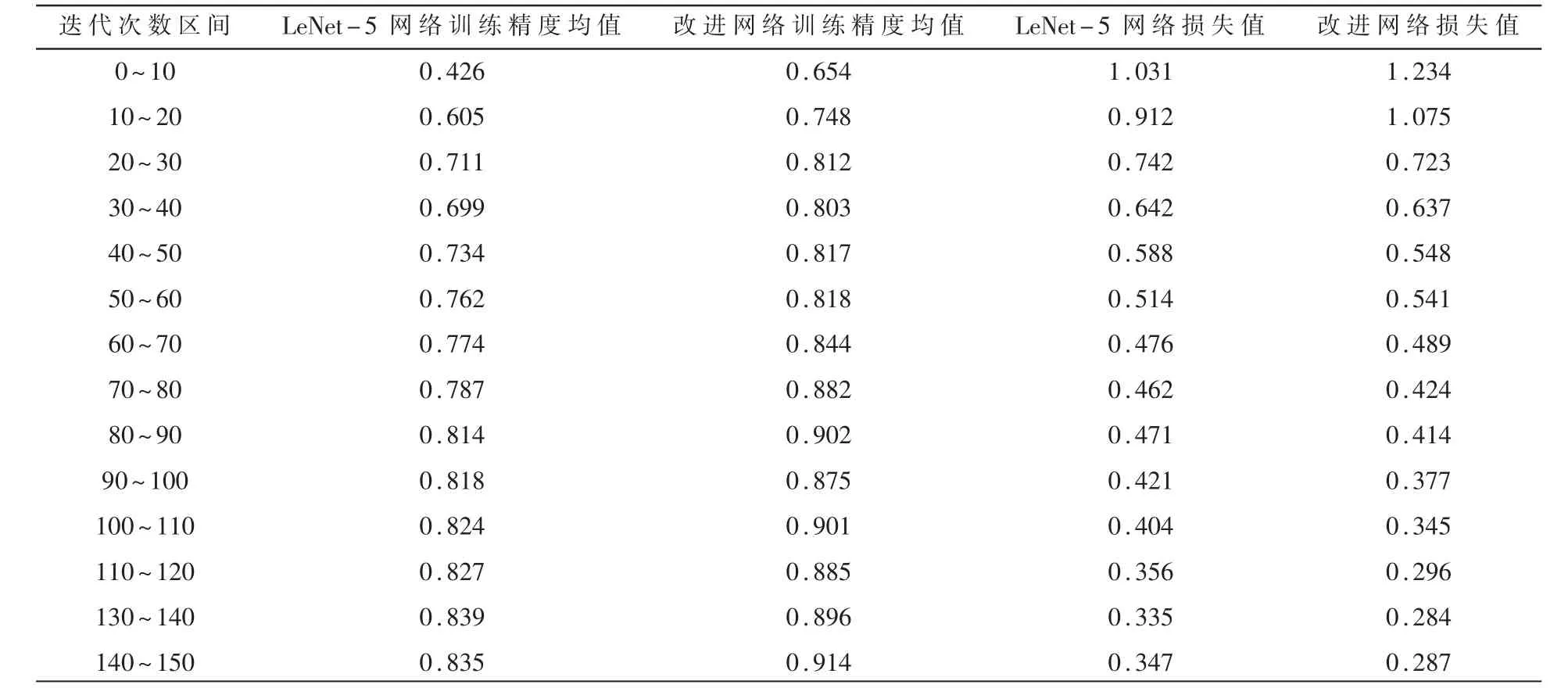
表3 两种网络区间迭代的训练精度均值与损失值变化表

表4 两种模型平均测试精度
由表4 可看出,经过网络的训练,10 次实验得到的未改进的LeNet-5 网络对测试样本的平均识别精度为0.754,改进后的网络对测试样本的平均识别精度为0.837。 因此,本文通过对LeNet-5 网络进行改进,有效提高了对于形状类似、硬度不同物体的识别精度。 上述表明,改进后网络不仅在训练精度上较原网络有所提升,而且能够在较少的迭代次数内达到收敛,且在识别精度上明显高于未改进的LeNet-5 网络。
4 结论
为了快速且高精度地识别形状类似、硬度不同的物体,提出了改进的LeNet-5 网络,在原网络的基础上,为了提高网络非线性变换的能力,将传统卷积层变为非对称卷积,为了减少参数,加入BN层,同时用全局平均池化层代替原Flatten 层, 利用数据增广增加样本集以减轻过拟合。 根据实验结果可知,改进的LeNet-5 网络较原网络能够以较低的迭代次数完成收敛,在训练精度与测试精度上较原网络有明显的提高。 说明改进型LeNet-5 网络对外形类似、硬度不同的物体有良好的识别效果,能够满足机器人柔性抓取力对物体识别精度的要求。

