基于障碍Lyapunov 函数的多智能体系统误差约束同步
吴慕兰
(中国科学技术大学 自动化系,安徽 合肥230026)
0 引言
近年来,多智能体系统由于在编队控制、无线传感器、机器人协作装备等领域的广泛应用而受到越来越多的关注。 作为多智能体系统研究中的基础问题,同步指所有智能体在某些变量例如位置或速度上达到一致的动态过程。目前存在的有关同步问题的工作主要分为两类:一类是无领航者的同步问题[1],一类是领航-追随者同步问题[2],并且其中大多数工作是关于线性系统的。但是在实际情况中系统不可避免地会出现各种非线性和不确定性项,因此未知非线性多智能体系统的同步已成为一个研究的热点。
由于神经网络方法[3-4]具有可以从样本集学习复杂映射的能力,其可以在线学习对未知非线性动力学系统的识别。基于神经网络固有的非线性逼近能力和内在的自适应学习特征,原始的控制问题常常可以转化为神经网络自适应控制问题[5-6]。 这类控制策略能保证系统的一致性误差最终可以稳定在一个较小的界内,其大小取决于模型中的一些显式参数和未知但有界的项,然而并没有系统的方法去计算这些上界,因此无法去准确地评估最终的稳定状态性能。 同时,不确定性使得控制过程中误差的收敛速度也难以准确地评估。 实际控制过程中,希望系统在各项参数设计好后满足给定的稳态性能和瞬态性能,即系统的误差最终收敛到给定的较小的界内, 同时收敛的速度不小于给定的值。KATSOUKIS T 等通过使用预设性能控制的方法来实现这一同步误差约束[7],其最终目标是使得每个智能体的同步误差严格地在预设区域内演化。 关键思想是通过转换后的同步误差将每个智能体的约束误差放宽为不受约束的误差,但是转换后的误差会增加需要处理的变量的数量且控制效果不稳定。
本文采用障碍Lyapunov 函数方法[8]解决误差约束问题从而避免引入转换误差,设计了新的分布式障碍Lyapunov 用以研究多智能体系统问题,实验结果表明同步误差能够被严格限制在预设范围内演化。
1 预备知识
1.1 图论

1.2 投影算子
投影运算常被用于自适应控制中约束被估计的参数,下面给出一类投影算子的定义。

对于N 维实向量θ,y ∈RN,投影算子Proj 的定义如下:其中标量函数φ:RN→R 是一个连续的凸函数,φ′(θ)是φ(θ)关于θ 的偏导数。
定 义 凸 集 合Ω0≜{θ ∈RN|φ(θ)≤0}以 及Ω1≜{θ∈RN|φ(θ)≤1}。 由文献[10]可知,在上文定义的投 影 算 子Proj(θ,y)和 初 始 值θ(t=0)=θ0∈Ω1下,θ永远不会超出集合Ω1。 同时对于任意的θ*∈Ω0和任意的y∈RN,下面的不等式成立:
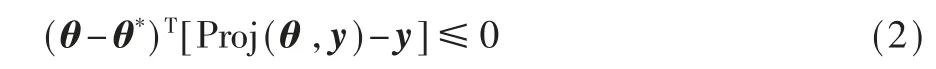
2 问题描述
给定一个由N 个追随者和一个标记为0 的领航者组成的多智能体系统。 第i 个追随者的动力学方程如下:
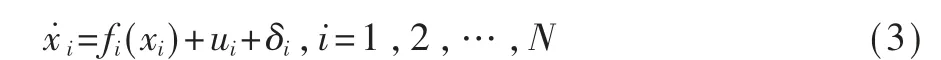
其 中,xi∈R 是 追 随 者i 的 状 态,ui∈R 表 示 施 加在追随者i 上的控制输入,δi∈R 是外界干扰因素,fi(xi)∈R 是满足局部Lipschitz 条件的非线性函数。
领航者根据以下动力学方程演变:

其中x0∈R 是领航者的状态。
本文的目的在于实现多智能体的同步,同时同步误差限定在给定的范围内以满足预期的瞬态和稳态性能。 为此,定义了邻居同步误差:
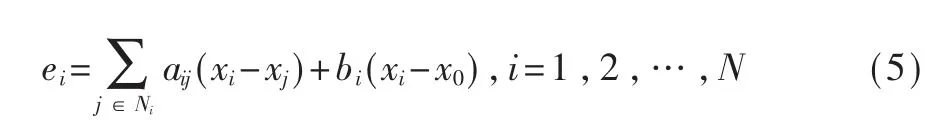
和与时间有关的性能函数:

其 中ρi0、ρi∞、mi是 根 据 初 始 条 件 和 期 望 性 能 选 择 的合适参数,期待达到的误差约束可以通过以下不等式说明:
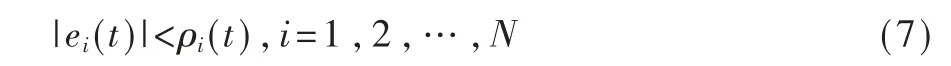
即希望误差ei的最大超调量不超过ρi0,最终收敛值小于ρi∞,收敛的速率不小于mi。
3 主要结果
3.1 人工神经网络


其中神经元的个数为vi,Wi∈Rvi是一个未知的理想权重列向量,其定义如下:

其中Si(xi)∈Rvi是一组基函数向量,多种类型的基函数如sigmoid 函数、 高斯函数都可以使用在神经网络中[5]。
真实的权重向量Wi值常常难以获得,采用估计值代 替则有:
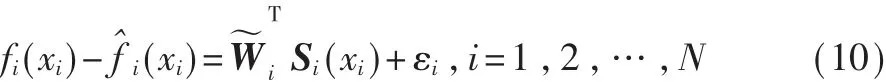
3.2 分布式障碍Lyapunov 函数
障碍Lyapunov 函数是自适应控制系统中常用来限制变量的工具。 它是一类定义在包含原点的开区域上的标量函数,一旦变量趋向于给定的边界,障碍Lyapunov 函数便会趋向于无穷大。 若能够设计合理的控制器保证障碍Lyapunov 函数是有界的,那么变量就会永远限制在给定的区域。 在介绍分布式障碍Lyapunov 函数之前,先给出一个相关的正定矩阵性质[11]。
令(L+B)是一个非奇异M-矩阵。 定义向量

和矩阵
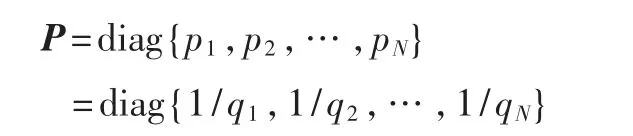
那么矩阵P 是正定的,同时定义矩阵Q 为
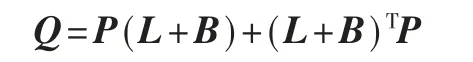
可以得到矩阵Q 也是正定的。
对于上文给定的邻居同步误差ei,接下来给出相应的分布式障碍Lyapunov 函数φ(e)RN→R+的表达形式如下:

其中e 为邻居同步误差ei组成的列向量,即e=[e1,e2,…,eN]T,并且有:
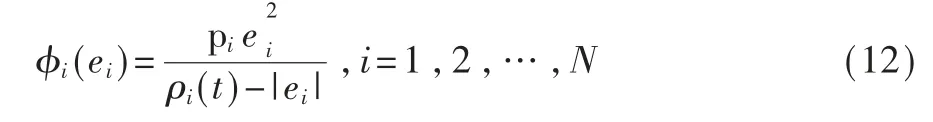
φ(e)对时间t 求导可以得到:

其中矩阵
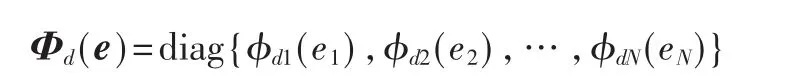
矩阵对角元素
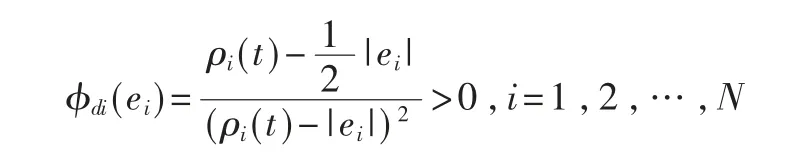
矩阵

矩阵对角元素

3.3 基于DBLF 的自适应控制律设计
基于前面提出的分布式障碍Lyapunov 函数,接下来给出第i 个追随者的控制律如下:
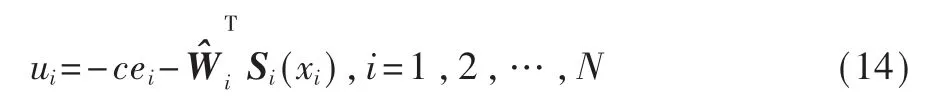
其中控制增益c>0。 基于定理1 的稳定性分析,局部神经网络的权重更新律如下:

其中di、bi和pi定义分别如上文矩阵D、B 和P 所示,矩 阵Ri=ΠiIvi∈Rvi×vi,待 设 计 的 参 数Πi>0。 1.2小节投影算子Proj 定义中的θ 对应这里的Wˆ,y 对应 这 里 的RiSi(xi)eiφdi(ei)pi(di+bi)。

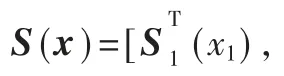

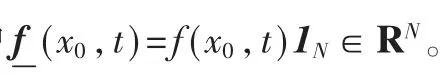


式(19)对时间t 求导可以得到:
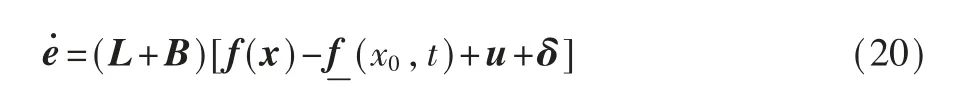
将式(16)代入式(20)得到:
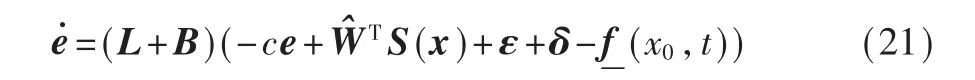
在给出定理1 之前,对系统有如下假设:
(2)各个多智能体干扰量组成的列向量δ 有界,即||δ||≤δM。
(3)神经网络基函数向量满足||S(x)||≤SM,权重估计值矩阵满足||W||F≤WM, 神经网络近似误差满足||ε||≤εM。
定理1:考虑由式(3)、式(4)定义的多智能体系统,其通信拓扑包含一棵以领航者为根节点的有向生成树。已知|ei(0)|<ρi0,i=1,2,…,N,ρi(t)是如前文所提到的性能函数(6),并且有:
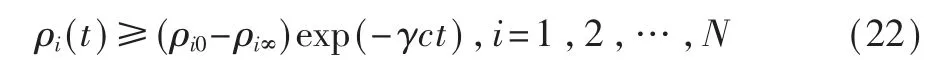
证 明: 考 虑 一 个 在 集 合Dρ×∈RviN上 定 义 的Lyapunov 函 数V:Dρ×∈RviN→R+如 下:
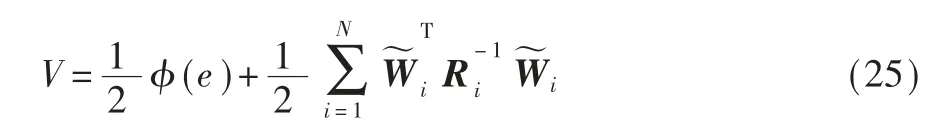
其 中,Dρ≜{e|e=[e1,e2,…,ei],ei∈(-ρi(t),ρi(t))},φ(e)是分布式障碍Lyapunov 函数(11),W~i是神经网络权重估计误差向量,Ri是神经网络权重更新律(15)中的对角矩阵。 利用Frobenius 范数,式(25)可以写成:

其中R=diag{R1,R2,…,RN}。 式(26)关于时间t 的导数为:·
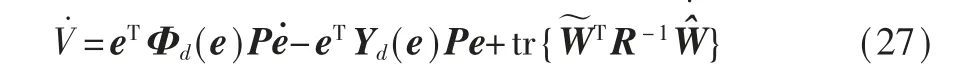
将式(21)代入式(25)得到:
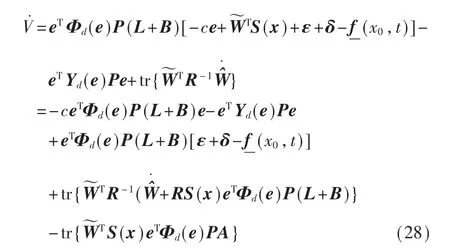
应用神经网络权重更新规则(15)以及相关性质(2),可以得到:
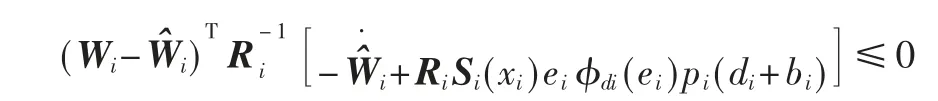
因此由式(28)得到:
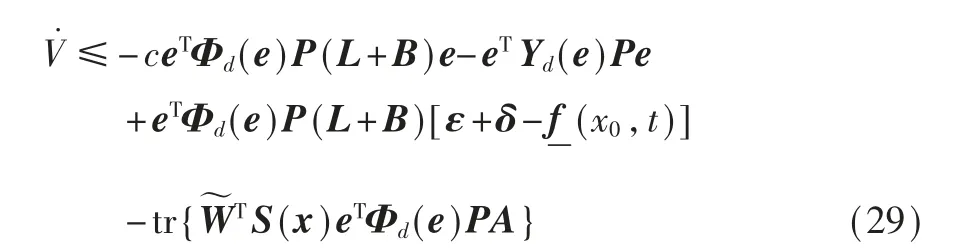
令α+β=1,0<α<1,那么不等式(29)可以写成:
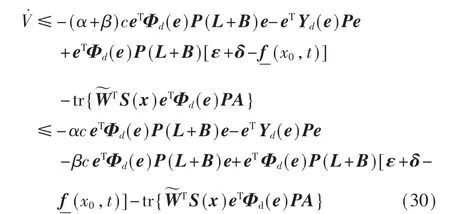

利用式(13),式(31)中的γcΦd(e)+Yd(e)可以写成对角阵的形式:

其中对角元素:
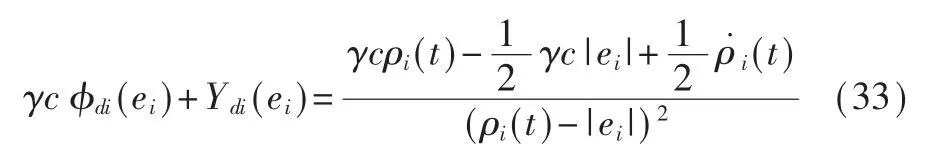
由ρi(t)≥(ρi0-ρi∞)exp(-γct)可 以 得 知,
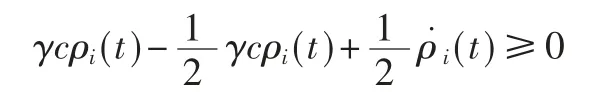
这确保了
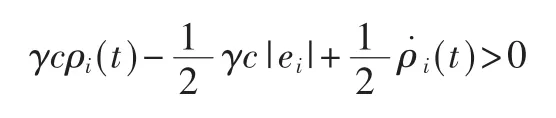
那 么 立 即 能 够 得 到γc φdi(ei)+Ydi(ei)>0,i=1,2,…,N。 因此γcΦd(e)+Yd(e)>0,不等式(31)可以放缩为:

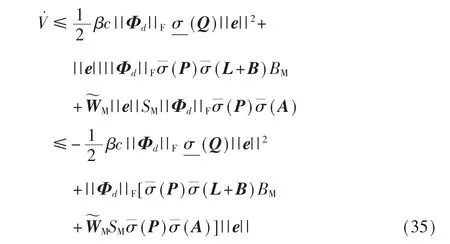
其中
因此,V˙≤0 的充分条件为:
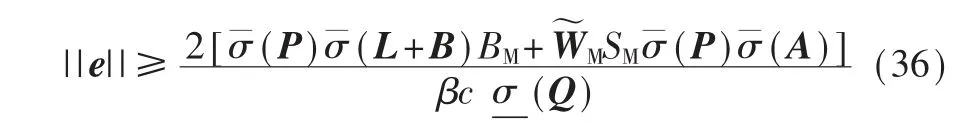
利 用 初 始 条 件|ei(0)|<ρi0,|ei(t)|<ρi(t)∀t ≥0 可以由文献[8]中引理1 得到。证毕。
4 仿真研究
为了验证所提出的的分布式自适应控制律的有效性,本文考虑图1 所示的通信拓扑,其包含5个跟随者和一个领航者,通信拓扑包含一棵以领航节点为根节点的有向生成树,边的权重都设为1。
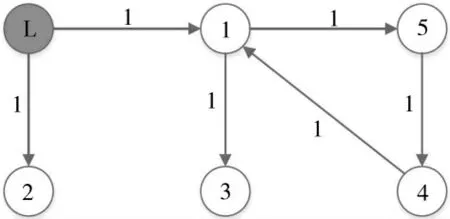
图1 多智能体系统的通信拓扑
首先,考虑文献[4]中提出的分布式自适应控制律:
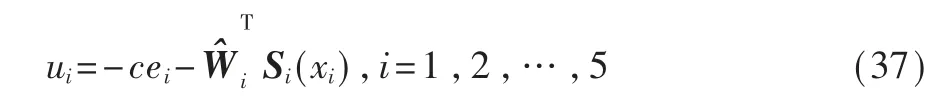
其神经网络权重更新律为:
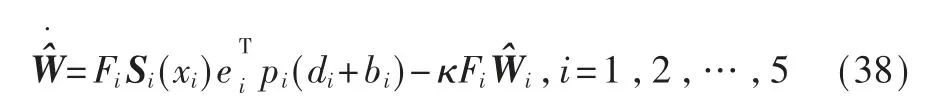
其中,参数Fi=1 500,c=225,κ=0.01,此外第i 个节点的神经元的个数选择为vi=3。 系统状态和局部邻域同步误差如图2、图3 所示。
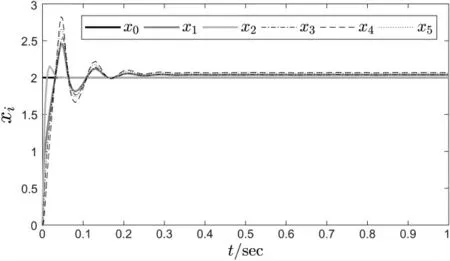
图2 采用控制律(23)和神经网络权重更新律(24)时的状态值
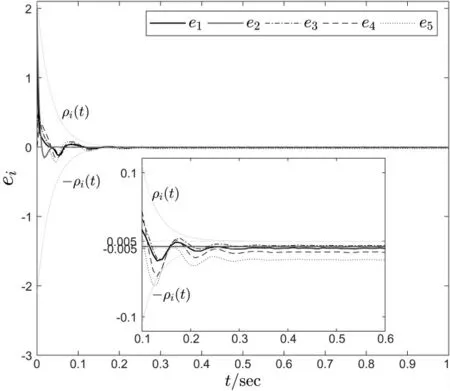
图3 采用控制律(14)和神经网络权重更新律(15)时的状态值
接下来,采用本文提出的基于DBLF 的自适应控制 律。 参数Πi=150,c=225,DBLF 的参数为ρi0=2.1,ρi∞=0.005 和mi=30,即:
ρi(t)=(2.1-0.005)×exp(-30t)+0.005,i=1,2,…,5
使用本文的自适应控制律的系统状态和局部邻居同步误差如图4 和图5 所示。
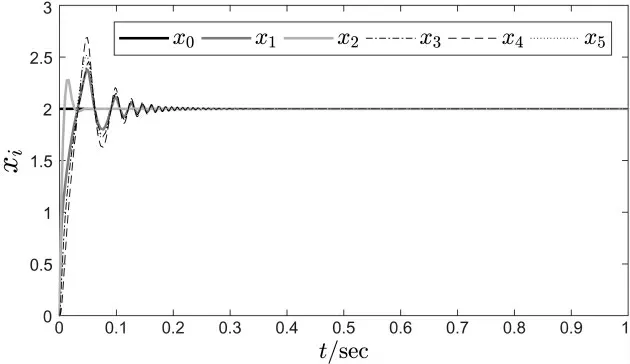
图4 采用控制律(23)和神经网络权重更新律(24)时的误差值
5 结论

图5 采用控制律(14)和神经网络权重更新律(15)时的状态值
本文研究了领航-追随者多智能体的同步误差限制问题,其中智能体动力学具有未知的非线性和不确定的干扰。 为了实现同步误差约束,本文开发了一种新颖的分布式障碍Lyapunov 函数,然后提出了基于分布式障碍Lyapunov 函数的神经自适应控制律。 最后用仿真实例证明了所提出协议的有效性。

