含微孔涂层的红外辐射特性数值计算及低辐射设计

王兴一，张成军，李明俊，朱洪立，于名讯，潘士兵

(山东非金属材料研究所，济南 250031)

红外探测及制导技术广泛应用于军事领域，开展目标在背景中的热红外辐射特征研究具有越来越重要的意义[1]。目前，热红外伪装隐身技术[2]研究方向主要是调整目标表面红外辐射率呈梯度形式，当目标表面温度以表观温度分布在热探测器上时，目标热红外图像呈迷彩形式，降低目标轮廓在背景中的可识别性[3]。传统的低辐射率导电涂层[4]会降低雷达吸收性能，特别是毫米波吸收性能，因此，研究非导电型涂层的低辐射特性具有重要意义。笔者采用微泡为填充物，分散在树脂材料中，研究此类非导电型材料的红外辐射特性[5]，为红外隐身材料的设计提供理论依据。

1 涂层辐射特性的理论依据

在真空中传播的一束平行单色光，若光束中存在一个小粒子，会产生散射现象[6]。入射波长与粒子尺寸处于同一个数量级时，粒子有很强的散射性，一般称之为谐振现象，谐振区散射有很大的应用潜力[7]。但谐振区散射的数学处理较为复杂。目前，三维物体的电磁散射麦克斯韦方程组[8]的解析求解，只局限在旋转椭球坐标系、球坐标系等坐标系，即标量波动方程解可以分离变量的坐标系。使用Mie 理论[9]可求解散射问题在球坐标系下的解。Mie 理论处理的问题为一个独立的任意大小的光学各向同性的球对任意波长入射波的电磁散射问题。

单色平面电磁波入射半径为a 的球形粒子(非磁性散射体)，发生散射。将散射波用矢量球谐函数展开，得到其散射波的展开系数为[10]：

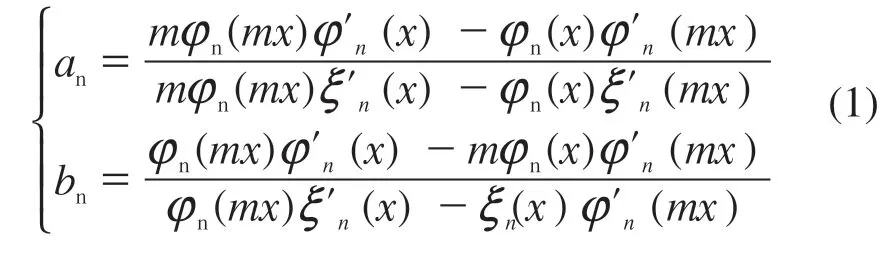
式中，n=1，2，3……为自然数，x=2πNha／λ为球形粒子尺寸，m=Np／Nh为粒子相对折射率，其中Np为粒子折射率，Nh为粒子所处环境折射率，λ为入射波在真空中的波长；散射系数an代表n阶电模或横磁模对散射电场与磁场展开式的贡献，bn代表n阶磁模或横电模对散射电场与磁场展开式的贡献。和是Riccati-Bessel 函数，用球Bessel 函数和第一类Hankel 函数表示其定义式为：式中为球Bessel 函数，为第一类球Hankel 函数[11]。

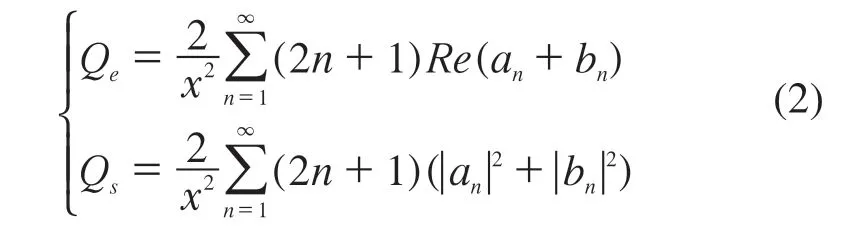
粒子的吸收效率Qa为其消光效率Qe与散射效率Qs之差。在光散射理论中，描述散射强度角分布的量被称为相函数，对确定光散射性质具有十分重要的意义。另一个重要物理量为粒子的前向散射率，它指的是一束平面波的照射下，散射体散射到粒子前半球方向的强度占前后半球总辐射强度的比例。Chylek 把相函数用散射系数展开后，得到前向散射率σc的解析表达式[7]：

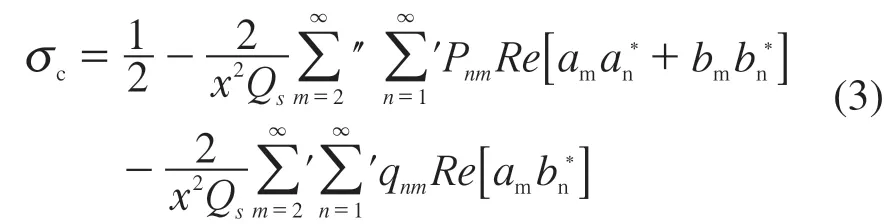
其中∑''为偶数项求和，∑'为奇数项求和。Pnm和Qnm分别为自然数n与粒子相对折射率m的函数。

1931 年，Kubelka 和 Munk 唯象地提出两个二元线性微分方程，建立了二流模型[12-13]，用于讨论涂层、胶体等浑浊媒质的光学现象。标准应用条件下，K–M 理论的吸收系数K和散射系数S的表达式如下[7]：

其中f为微泡的体积分数，定义物理量Rv与γ为：

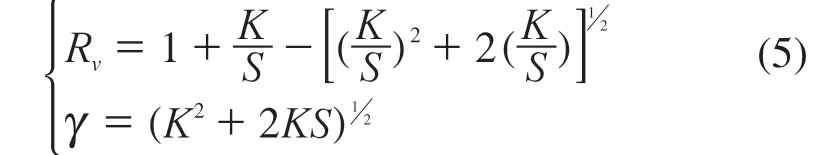
一般涂层下面有底漆，底漆覆盖在金属基材上。当光从外侧照向涂层时，面层和空气之间反射率为Re，面层和底漆之间的反射率为Rg，面层内侧的反射率为Ri。设涂层相对于入射方向媒质的折射率为m1，前界面的内外漫反射率的关系为Ri=1-(1-，则有：

根据以上各式，最终得出涂层辐射率计算公式为：

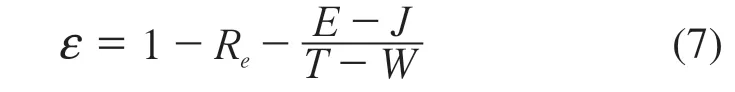
式中，E，J，T，W为对反射率做数学运算产生的物理量。E为

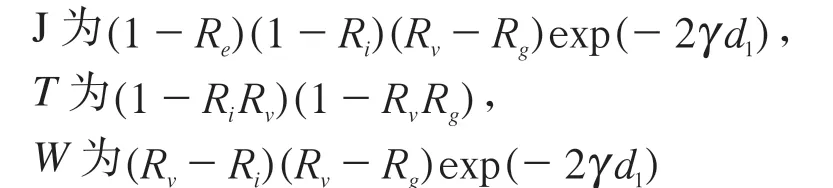
其中，d1为涂层的厚度，Rg为涂层在红外波段的漫反射率，一般底漆的辐射率很高，可认为Rg≈0.1。从上述公式可知，影响涂层红外辐射率因素包括涂层厚度、树脂折射率[14]、微孔尺寸与微孔体积分数。

2 模拟计算

当填充物为气泡时，设气泡直径为10 μm，入射波长为20 μm 时，采用式(3)可得到气泡的前向散射率为0.83。同样条件下，采用ANSYS 软件计算了粒子后向散射率(–90°至90°的能量与全角度能量之比)，结果为0.18(如图1 所示)，即粒子的前向散射率为0.82。由MIE 散射得到的数据与ANSYS 软件模拟得出的数据极为接近。

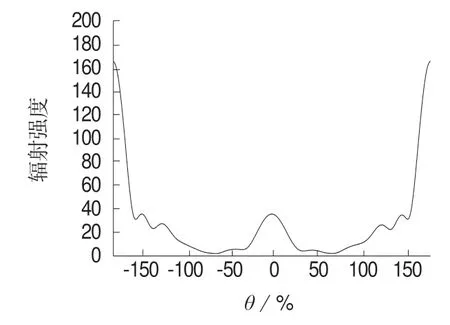
图1 不同散射角度下的红外辐射能量

2. 1 涂层厚度对红外辐射率的影响

在红外波段，假设树脂折射率为1.6+0.2i，当微孔体积分数为0.9，计算了涂层厚度d1对红外辐射率的影响，如图2 所示。

图2 涂层不同厚度时红外辐射率

由图2 可见，当涂层厚度较小时，涂层具有较高的红外辐射率；随着涂层厚度不断增加，涂层的红外辐射率逐渐下降，至涂层厚度达到400 μm时，红外辐射率降低至0.88；此后，涂层厚度继续增加，红外辐射率不再发生变化。即涂层厚度达到400 μm 或更高时，表现出面层本身的辐射特性。

2．2 微孔尺寸、树脂折射率对涂层红外辐射率影响

当材料折射率m=n+ki中，k 为 0.2，n=1.45，1.55，1.65 时，计算了微孔尺寸对涂层红外辐射率的影响，结果如图3a 所示。同样，当n=1.6，k=0.10，0.15，0.20 时，微孔尺寸对涂层红外辐射率的影响结果如图3b 所示。由图3a 可以发现，树脂折射率1.45+0.2i时，发生Mie 散射的谐振区的微孔尺寸为93～205μm，在此区间，材料的辐射(反射)随颗粒尺寸剧烈波动，是强谐振区，此区间内的平均辐射率为0.82。分别计算图3a、图3b 中不同折射率下，材料谐振区间内的平均辐射率，得表1。

图3 不同树脂折射率下微孔尺寸不同时涂层辐射率

表1 不同折射率下材料在谐振区间内平均辐射率

由表1 分析可得，当折射率虚部相同时，实部增加，谐振区间向微孔尺寸变小的方向发展，实部由1.45 增加到1.65，谐振区间起始微孔尺寸由93μm下降到40μm。当折射率实部相同时，虚部增加，谐振区间亦向微孔尺寸变小的方向发展，虚部由0.1i增加到0.2i，谐振区间起始微孔尺寸由70 μm 下降到40 μm，同时材料的平均发射率由0.87 下降到0.84。表1 中谐振区间的范围较大，且由图3a、图3b 中可以发现，谐振区间内存在一定的微孔尺寸范围，使得材料具有较低的辐射率。缩小谐振区间范围，计算区间内的平均辐射率，寻找低辐射率的谐振区间。计算结果见表2。由表2 可以发现，缩小谐振区间范围，即选取合适的微孔尺寸范围，可以得到较低的平均辐射率。树脂折射率1.45+0.2i时，微孔尺寸140～188μm 区间材料有最低平均辐射率0.77；树脂折射率1.55+0.2i时，微孔尺寸120～140μm 区间材料有最低平均辐射率为0.76；树脂折射率1.65+0.2i时，微孔尺寸85～100μm 区间材料有最低平均辐射率为0.69。当树脂折射率虚部不变时，实部增加，谐振最强区间向微孔尺寸变小的方向发展，且微孔尺寸分布更窄，平均辐射率可降低至0.7 以下。

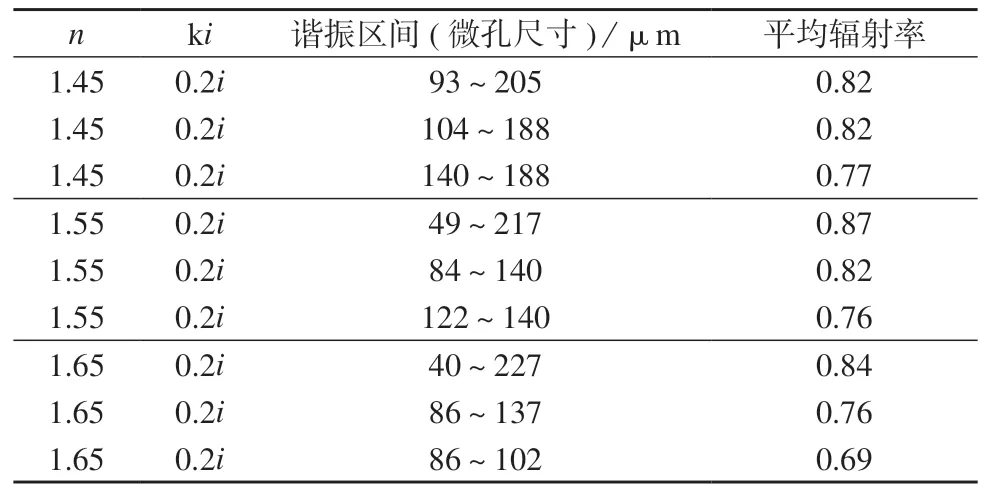
表2 不同折射率实部下材料在谐振区间内平均辐射率

表3 不同折射率虚部下材料在谐振区间内平均辐射率

由表3 可以发现，折射率虚部较小时，共振强度小，平均辐射率较高；虚部增加，共振强度增加，平均辐射率下降。控制微孔尺寸分布范围，使其位于共振增强区间，可得到更低的红外辐射率。折射率为1.6+0.1i时，微孔尺寸182～220μm 区间材料有最低平均辐射率0.82；折射率为1.6+0.15i时，微孔尺寸49～70μm 区间材料有最低平均辐射率0.81；折射率为 1.6+0.2i时，微孔尺寸 89～100μm 区间材料有最低平均辐射率0.69。虽然虚部为0.15 时，最低平均辐射率谐振区间在微孔尺寸更小的位置，但虚部为0.2 时，材料在89～100μm 具有最低平均辐射率。

由表2、表3 分析可得，树脂折射率实部与虚部均确定，控制微孔尺寸分布范围，可以得到低辐射率。折射率实部、虚部分别增加时，控制微孔尺寸分布范围更窄，可以得到更低的红外辐射率。

2．3 微孔浓度对涂层红外辐射率的影响

根据公式(4)，红外涂层体积分数f与涂层红外辐射率关系如图4 所示。

图4 涂层红外辐射率与微孔体积分数的关系

从图4 可知，树脂折射率为1.6+0.2i，涂层厚度为2 mm，当微孔体积分数为零时，相当于只有树脂材料，底层材料辐射率高，同时树脂的高辐射率使得整个涂层的红外辐射率很高。随着微孔体积分数增加，涂层的红外辐射率逐渐降低。微孔体积分数提高至15%时，涂层红外辐射率降低至0.86。继续提高微孔体积分数不再对涂层的红外辐射率产生影响。最终，提高微孔体积分数使得涂层的红外辐射率由0.906 下降至0.86。

使用ANSYS 软件进行模拟。模拟结果显示，在微孔含量达到14%以后，涂层的红外辐射率保持平稳，为0.860。此结果与MATLAB 计算结果相吻合。

3 结论

采用Mie 散射和Kubelka-Munk 二流模型的涂层红外辐射率理论模型，给出了当填充物为气泡时，树脂折射率、微孔尺寸、微孔体积分数、涂层厚度对涂层红外辐射率影响的规律。

(1)树脂折射率的实部与虚部影响涂层的红外辐射率。实部增高，谐振区明显向微孔尺寸变小的方向发展，同时谐振增强；虚部增高，谐振增强，平均红外辐射率越低；

(2)微孔尺寸对于涂层的红外辐射率具有较大影响。精确控制微孔的尺寸分布是得到低辐射率材料的重要途径。

(3)随着微孔体积分数增加，涂层的红外辐射率逐渐降低。微孔体积分数增加到15%以后，涂层红外辐射率不再降低。

(4)随着涂层厚度增加，涂层的红外辐射率会逐渐降低。当厚度达到400 μm 后，涂层厚度的继续增加不会再降低涂层的红外辐射率。