临床研究缺失数据多重填补敏感性分析方法＊

闫世艳，郭中宁，何丽云，刘保延

（1.中国中医科学院中医临床基础医学研究所 北京 100700；2.中国中医科学院西苑医院 北京 100091）

缺失数据是医学研究中的常见问题，当缺失数据较多时，若不进行处理往往会导致信息损失、降低检验效能导致结果偏倚。在统计分析中，缺失数据的处理是非常重要的内容。处理缺失数据，首先要明确数据的缺失机制。通常将缺失数据机制划分为三类：完全随机缺失（Missing Completely at Random，MCAR）、随机缺失（Missing at Random，MAR）和非随机缺失（Not Missing at Random，NMAR）[1]。不同缺失机制的处理方法不同。对于完全随机缺失，可以忽略缺失数据，即不对缺失数据进行处理，直接应用完整观测到的数据进行分析。目前的统计分析软件中，默认采用的都是这种形式，但实际情况中完全随机缺失的情况非常少见。

大多数的缺失数据处理方法是针对随机缺失机制的，随机缺失数据的处理方法可以分为三大类：直接推导法、填补法和重复抽样法。一般较为常用的是填补法（Imputation），即给每个缺失数据一些替代值，这些替代值称为填补值。根据填补值个数，又可以分为单一填补（Single Imputation，SI）和多重填补（Multiple Imputation，MI）。目前，临床研究中常用的单一填补方法是末次访视观察值向前结转（Last Observation Carried Forward，LOCF），该方法操作简单方便，在国内应用普遍。多重填补是对每一个缺失值用多个可能的值进行多次填补，考虑了缺失值的不确定性，与单一填补相比更为合理，被很多杂志所推荐。非随机缺失时，缺失数据的处理会比较复杂，但也有专门的缺失值处理方法。在上述三种缺失机制下，当假定数据符合随机缺失机制进行填补后，通常需要进行敏感性分析来验证该假定下填补结果的可靠性和稳健性。在实际情况中，研究者往往无法验证随机缺失的假定是否正确。美国研究委员会（National Research Council）建议在临床试验中，对于假定缺失数据为随机缺失的研究，应进行敏感性分析，并且敏感性分析应该是研究报告必须报告的内容[2]。

目前，多重填补的方法在国内外已经逐步得到广泛的应用，有不少相关的方法学研究文献[3-7]，但研究者对其敏感性分析的问题并不了解和重视，也缺乏相关方面的报道和文献。本课题组查询了中国知网（CNKI）、维普等主流中文文献数据库，并未发现有关多重填补敏感性分析的资料和文献，相关的英文文献也比较少。有研究者就国内针刺临床试验缺失数据的报告情况及其对结果的影响进行调查分析发现，3008篇RCT报告中仅有343篇（11.4%）报告了数据缺失原因。纳入报告中仅有63篇（2.1%）提及了意向性分析，且只有30篇（1.0%）报告了意向性分析结果。对报告了分类结局变量的两臂试验数据的二次分析结果表明108篇（30.2%）研究与原始结论不一致；92篇（85.2%）可能存在假阳性结果，16篇（14.8%）可能存在假阴性结果。该研究反映了国内临床研究者对缺失数据的重视和认识程度较低,大多数研究未采用合理的缺失数据处理方法，更没有研究提到缺失数据的敏感性分析[8]。因此，本研究将就多重填补的敏感性分析原理和方法进行简要介绍，并给出相应的实际应用案例，以期为相关临床研究者提供参考和帮助。

1 多重填补敏感性分析的基本原理

一般情况下，多重填补时，假定数据缺失机制为随机缺失，且数据符合多元正态分布。按照随机缺失的假设，可得出：

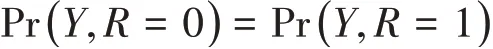
其中Y表示目标变量的值，R表示缺失与否，R=1表示缺失，R=0表示非缺失。由此可见，随机缺失机制下，缺失数据的分布与观察到数据的分布相同，因此可以基于观察到数据的分布产生缺失数据的填补值Y(1),Y(2),…Y(k)。

但是，随机缺失假定在实际情况下是无法进行验证的，本研究须对基于随机缺失假定下的多重填补分析结果进行敏感性分析，即在违背随机缺失假定下进行分析，以验证随机缺失假定下多重填补分析结果的稳健性。该敏感性分析的基本思路为构建一个非随机缺失模型，基于该模型产生缺失数据的填补值，然后进行多重填补，得到非随机缺失机制下目标变量的效应估计值，然后对随机缺失机制与非随机缺失机制下的多重填补结果进行比较，若非随机缺失机制下的多重填补结果与随机缺失机制下的结果一致，则认为随机缺失的假定是合理的。反之，则认为随机缺失的假定不合理。

2 多重填补敏感性分析的基本步骤

多重填补敏感性分析的过程与多重填补的完全相同，主要区别在于产生缺失数据的填补值所基于的分布不同。以下为多重填补敏感性分析的基本步骤。

第一步，产生缺失数据的填补值：与随机缺失不同，在非随机缺失机制下，缺失数据的分布与观测到的数据分布不同，即

因此，非随机缺失机制下不能基于观测到的数据分布产生缺失数据的填补值。

本研究再分析一下纵向临床研究中的情形。假设G表示组别，G=1为试验组，G=0为对照组；Y表示某次访视该目标变量的值，当Y的缺失符合随机缺失时，则有[9-10]：

和

当Y的缺失符合非随机缺失时，则有：

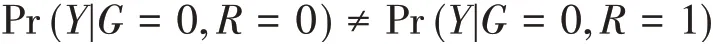
和

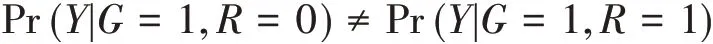
基于上述情形，非随机缺失情况下，可通过以下两种方式构造非随机缺失的填补模型：

第一种方式：不管是试验组还是对照组的缺失值，均基于对照组中观察到数据的分布产生填补值，即

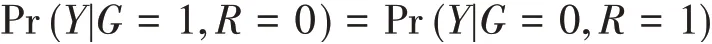
第二种方式：在随机缺失假定的填补模型中加一个不为0的调整参数δ，即

调整参数δ反映的是观测到的数据与缺失数据的总体参数的差值，一般通过与临床研究者讨论并结合专业知识确定。δ值的绝对值越大，说明缺失数据的分布与观测到数据的分布之间的差异越大。若在极端情况下，即δ已经超过临床实际可能发生的情况时，此时多重填补得到的分析结果仍与随机缺失情况下的一致，则认为随机缺失假定下进行多重填补得到的分析结果是可靠的；反之，则说明随机缺失的假定是有问题的，在此假定下推断的分析结果不可靠。

表1 两组治疗8周期间每周的CSBMs（次/周）描述

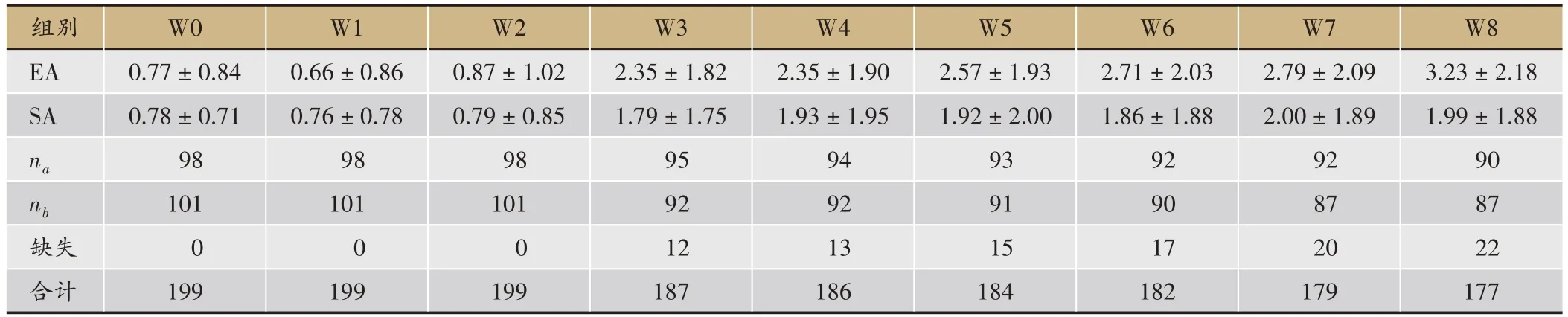
表1 两组治疗8周期间每周的CSBMs（次/周）描述

注：*W0为基线，W1-W8分别表示第1-8周

?

表2 基线及1-8周CSBMs的缺失模式描述和分析

第二步：对缺失数据集进行m次填补，产生m个填补好的“完整数据集”，对每个填补后的“完整数据集”分别采用合适的统计方法进行分析，得到每个“完整数据集”对应的参数估计值等指标。

第三步：根据一定的规则将m组统计分析结果进行综合，得出最终结论。例如，设目标变量的总体参数为θ和σ2，其点估计分别是̂和̂，对每个填补后的数据集进行分析，得到(θ1,σ12)，(θ2,)……(θm,)，然后采用Rubin法则进行综合，得到综合后的估计值[11]，并将结果与多重填补的分析结果进行比较。

在多重填补的敏感性分析中上述方法较为常用，被美国医学会杂志(Journal of the American Medical Association，JAMA)，内 科 学 年 鉴(Annals of Internal Medicine)等高影响因子杂志所推荐[12-14]。在SAS统计分析软件中有相应的方法，可通过软件实现。

3 应用案例[13]

通过一个实例对上述多重填补敏感性分析方法进行验证。为评价电针治疗严重性便秘的疗效，某医院进行了一项大样本多中心随机对照临床试验，将符合纳入排除标准的受试者随机分配到电针组（EA）和假电针组（SA），治疗8周。主要疗效指标为治疗8周后的周平均完全自主排便次数（CSBMs）。现截取前199例数据为例，其中177例受试者完成全部试验，22例受试者提前中止临床试验（失访12例，因不良事件退出试验5例，患者自动退出5例）。表1为基线和第1-8周的周平均CSBMs以及各数据的缺失情况。

3.1 对缺失值进行多重填补

第一步，判定数据的缺失模式，对表1中基线到8周的CSBMs，即W0-W8周CSBMs是否缺失进行汇总分析，得到表2，可见W0-W8周CSBMs的数据缺失符合单调缺失模式，即受试者在某个时间点缺失后，其后面的数据都是缺失的。两组间的缺失模式经Fisher确切概率检验，差异无统计学意义（P=0.088）。

第二步：对缺失值进行填补，并进行分析，得到多重填补后的分析结果。假定数据缺失机制为随机缺失，考虑到疗效指标周平均CSBMs是计量资料，且符合单调缺失模式，采用参数回归法对1-8周的CSBMs缺失值进行填补。

考虑到周平均CSBMs的特点和可能的影响因素，在填补的回归模型中纳入如下变量：基线CSBMs值、每周CSBMs值、年龄、性别、应急药物和其他便秘辅助措施使用情况。设m=5，即共产生5个填补后的“完整”数据集。对5个填补后的“完整”数据集，采用协方差进行分析（应变量为治疗8周后CSBMs相对基线的变化值，设研究中心为固定效应、基线CSBM为协变量），得到5个分析效应的估计值以及其综合后的估计值，见表3。填补号列中的原始数据表示没有进行缺失处理时的分析结果；填补号1-5分别表示5个填补后数据集的分析结果，综合表示5个填补后数据集综合的分析结果。根据表3可知，没有进行缺失值处理时，即采用“完整数据”进行分析的结果为：EA组的治疗8周后CSBMs相对基线的变化值为2.58（95%CI:2.16-3.00）次，SA组为1.21（95%CI:0.79-1.63）次；EA组与SA组间的差值为1.37次（95%CI:0.77-1.96）。多重填补后EA组的治疗8周后CSBMs相对基线的变化值为2.51（95%CI:2.10-2.92）次，SA组为1.40（95%CI:1.00-1.81）次；EA组与SA组间的差值为1.10次。未填补的原始数据分析结果、5个填补数据集的分析以及综合分析的结果均表明主要疗效指标的组间差异有统计学意义（P＜0.05）。

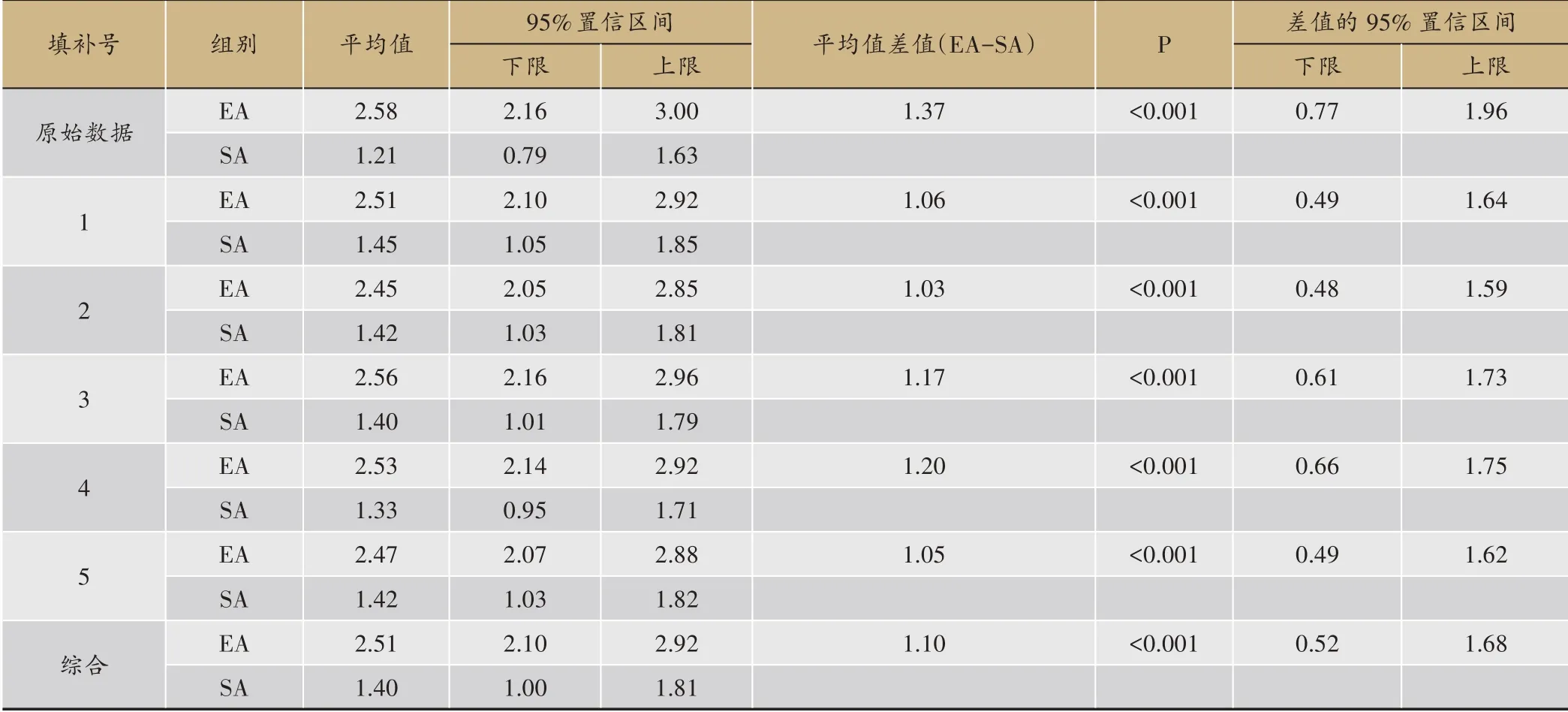
表3 填补前、后以及综合的主要疗效指标估计值及组间差值

3.2 对多重填补结果进行敏感性分析

首先，构建非随机缺失的填补模型。为体现非随机缺失的特点，设定基于对照组（SA组）数据的分布产生缺失数据的填补值，同时在填补值产生模型中设定调整参数δ。通过与临床研究者讨论，对于周CSBMs来说，如果便秘患者一周超过8次，显然不符合严重性便秘的诊断和正常的临床常识，故本研究将调整参数δ确定为8。产生填补值过程中的其他设置均与多重填补完全相同。然后，对缺失值共进行5次填补，对填补后的5个完整数据集采用与多重填补相同的协方差分析方法进行分析，参数设置完全相同，最后得到填补后的综合分析结果。表4表示，基于对照组（SA组）观测到数据的分布对缺失数据进行多重填补，并在填补模型中设定调整参数δ，δ不同时周平均CSBMs的估计值的变化情况。可以看出，主要指标周平均CSBMs差值的估计值随着调整参数δ的增大而逐渐减小。当调整参数δ为8时，分析结果是最极端的，其中两组主要指标周平均CSBMs差值的估计值为0.42次，95%CI为（0.05，0.79）次，差别仍有统计学意义。该结果与随机缺失假定下的分析结果（表3）是一致的，说明进行多重填补时关于随机缺失的假定是可靠的，多重填补分析的结果（表3）是可靠的。

表4 基于SA组数据进行填补并设定调整参数δ时，不同δ情况下的主要指标估计值及其95%CI

4 讨论

在临床研究中，缺失数据是不可避免的一个重要问题。对于缺失数据，首先应该进行预防，即通过严谨的研究设计、严格的质量控制以及仔细的数据清理等各项措施尽可能的减少。对于经过上述过程，仍然存在的缺失数据，再通过合适的统计学方法进行填补和处理，以避免由于数据缺失带来的偏倚。缺失数据处理时要考虑数据缺失机制和数据缺失模式，对于完全随机缺失的数据，可以不加处理，直接采用完整的观测值进行分析。但在实际临床研究中，真正的完全随机缺失很少见，更多的是随机缺失和非随机缺失。在进行缺失数据处理时，通常在随机缺失假定下进行处理。大多数的缺失数据处理方法是在该假定下。

目前，国内的临床研究者对缺失数据的处理并未引起足够的重视，大多数的医学杂志发表的临床研究论文直接忽略掉缺失数据，直接采用完整数据进行分析；或者并未给出缺失数据是否处理以及具体的处理方法。而在进行了缺失值处理的文章中，则以末次访视向前结转的方法为主，这也是目前国内主流的和最为常用的缺失数据处理方法。末次访视向前结转属于单次填补，与多重填补相比，该方法简单方便，但未考虑缺失值的不确定性。

近年来，多重填补的方法应用越来越多，已经得到了较为广泛的接受，很多高影响因子杂志均要求采用多重填补的方法进行缺失值处理[16]。由于多重填补基于随机缺失假定，而实际情况下，随机缺失假定无法进行验证。因此，对其进行违背随机缺失假定下的敏感性分析是非常必要的。但目前多重填补的敏感性分析并未得到重视，不管是中文文章还是英文文章，绝大多数在多重填补后并未进行敏感性分析，关于敏感性分析方法的介绍也非常少。本研究介绍了一种较为简便易行的多重填补敏感性分析方法，且已经应用在本文引用实例的临床研究中，并且该文章已发表在美国内科学年鉴杂志上。本研究所介绍的多重填补以及敏感性分析方法均通过SAS统计分析软件实现。

本研究的实例采用了基于对照组观测到的数据产生填补值，同时设定调整参数δ的方法来构建非随机缺失。在实际应用时，也可以仅采用其中一种方式。在设定调整参数δ时，应由统计学人员与研究者根据临床实际情况进行商讨决定。对于多重填补的次数，本研究实例进行了5次多重填补。通常来说，对于缺失信息比例在50%左右的变量，填补5次就可以获得很高的相对效率。但是，近年来也有学者认为填补的次数应该为20-100次[17]，当填补后的分析结果趋于稳定即可。另外，为保证填补值的可靠性，在进行构建填补模型时应尽可能地纳入以下三类变量：①分析中的关键变量；②对关键变量有预测性的协变量；③对缺失数据可能有预测性的协变量。因此，在设计阶段也应充分考虑哪些因素可能会与重要指标的缺失有关，并在研究过程中尽可能采集全面[17]。最后，在报告缺失数据处理结果时应注意尽可能包括如下内容：①数据缺失模式和机制。②缺失数据处理方法。详细报告多重填补的目标变量是哪些，产生填补值的具体方法，具体哪些变量被纳入在填补模型中；填补数据集的个数等；③填补后的统计分析方法及结果；④敏感性分析的方法、参数设置以及结果。另外，还要强调的一点是多重填补通常针对原始变量进行填补，而不是针对衍生变量。如本实例中，本研究对W0-W8每周的CSBMs进行填补，然后再根据公式（第1周至第8周的周CSBMs总和/8）计算治疗后8周的周平均CSBMs，而不是直接对治疗后8周的周平均CSBMs进行填补。因为治疗后8周的周平均CSBMs是基于W0-W8每周的CSBMs衍生计算出来的。