基于GA-PSO和时空特性的城市交通协同控制

陆百川,舒 芹,马广露,何相嶬

(1.重庆交通大学 交通运输学院,重庆 400074; 2.连云港杰瑞电子有限公司,江苏 连云港 222007)

0 引 言

随着城市的快速发展,城市道路交通越来越复杂,它不但会随着时间的变化而变化,还会受到空间因素的相互影响，因此,从时间维度与空间维度来分析交通流的特性,能更好地解决城市交通问题。同时,信息技术的发展,以及云计算、大数据、智能检测技术在交通领域的广泛应用,使得交通流数据的获取与应用更加方便[1]。通过对交通流数据的处理,分析交通流的时空分布规律及其相互影响[2],在时间上对节点交通流进行调控,在空间上对路网交通流进行分配的交通协同控制,将有效缓解城市交通拥堵。

在交通流的时空特性方面,文献[3]分别运用混沌理论与相关系数法分析了交通流的时间、空间特性,利用多维标度法对多断面交通流进行了聚类和分组,但是对时间、空间维度的交通流及其相互关系研究不足;文献[4]论证了城市交通流的空间相关性,指出上、中、下游交通流参数具有传递与回溯关系;文献[5]运用时间、空间序列的流量观测值作为支持向量机训练样本,使用空间预测值修正时间序列预测结果,建立了基于支持向量机与自适应时空数据融合的预测模型,但是对于时空数据序列的权重标定方法未作探讨。在城市交通协同控制方面,文献[6]以车均延误最小为目标,建立了信号控制与协同诱导的双层规划模型,但是缺少对拥堵交通流协同关系的研究;文献[7]引入平均速度与平均密度改进目标函数,采用罚函数与模型预测控制的思想,提出了多交通子区的协同控制方法,但是模型中忽略了上、下游交通流的相关性。

本文从城市交通流的时间与空间分布规律出发,综合分析交通流的时空变化特性,利用遗传算法(genetic algorithm,GA)与小波神经网络(wavelet neural network,WNN)分别对时间维度与空间维度的交通数据进行处理,并利用最小二乘动态加权算法对时空数据序列进行融合;基于时空相关的交通流融合数据,以时空饱和度与行程时间为约束建立了协同控制模型;结合GA全局搜索技术及粒子群优化(particle swarm optimization,PSO)并行寻优能力,设计了基于GA-PSO的协同控制求解模型。算例分析结果表明,考虑时空特性的城市交通协同控制能有效减小路网行程时间、优化交通控制参数、均衡路网交通分布。

1 交通流时空特性及协同控制分析

1.1 交通流时间变化特性

交通流时间特性是指某断面交通流状态在时间尺度上的变化规律。交通流在较长时间尺度(如1 a、1月)上有一定周期性,而在较短时间尺度(如1 h、15 min)内又具有时变性与相关性。

1 a内,交通流时间序列静态平稳性相对明显,但每月交通量大小、变化规律不尽相同,不同地区交通量变化曲线也并非完全一致;1月内,每周交通量存在一定的相似特性,按一定的规律进行变化;1周内,每日交通流会在相似的时段出现波峰与波谷,但工作日交通量普遍大于周末休息日交通量,并且出现高峰的时段也略有不同;1 d内,不同时段的交通流变化最为显著,本时段的交通流与前几个时段的交通流有明显联系,同时也会对后几个时段交通流产生影响。

1.2 交通流空间变化特性

交通流空间特性是指某时刻交通流在城市路网上的分布状况。观测断面交通流与连通可达的邻近路段交通状态具有相关性,从而使交通流具有时变性。

城市路网中,上游路段的部分车辆经过一定时间通过道路载体会行驶到下游路段,影响下游车辆的运行情况[8];下游路段的交通状态在一定时间后通过车流波动也会对上游交通产生作用,影响上游车辆的路径选择。城市道路上,不同地理位置、不同交通断面、不同行驶方向及不同车道间的交通流分布均有差别。交通流空间特性会随着上、下游交通驶入、驶出量以及车辆行驶离散性的不同而变化,进而影响着整个城市路网的交通状态波动与交通路径选择。

1.3 交通流时空变化特性

交通流时空特性是指城市路网中空间对象随时间序列的变化规律,强调交通流在时间维度和空间维度的相互联系。在时间上,每个时段交通流都在发生变化,下一时段的交通流可看成上一时段交通流在某种交通状态下的延续;在空间上,同一时段不同路段交通流也会变化,下游路段的交通流可由上游路段交通流估计而来[9]。综合分析交通流的时空特性,通过时空特性的交通流数据处理,能增强交通数据间的共享与互补,扩大交通数据的时空覆盖率。

城市路网中交通流的时空变化关系如图1所示。

图1 路段交通流时空关系图

设路段R为观测路段,则T0时段交通流不仅与路段R在T0-Δt、T0+Δt时段交通流有关,也与路段R-1、R+1在T0时段的交通流相关。由于上、下游交通流具有延迟性,路段R交通流与路段R-1在T0-Δt时段的交通流以及路段R+1在T0+Δt时段交通流都有内在联系。因此,路网交通流在时空维度相互关联、相互影响,分析并掌握交通流的时空分布特性,能更好地解决城市交通问题。

1.4 时空相关的城市交通协同控制

时空相关的城市交通协同控制是指利用交通流的时间相关性与空间相关性实施协同控制,以减小路网交通延误与实现交通流合理分配。

城市交通协同控制中,考虑交通流的时间相关性,在时间上对进入或驶离路网的车流进行强制性控制,以减少交通延误[10];同时,考虑交通流的空间相关性,对将要驶入路网的车流在空间上进行建议性引导,以均衡路网交通流量。协同控制能够在时间上调控节点车流量以及在空间上分配路网交通流,能够改变车流的时间分布与空间分布,能顺应交通流本身的时间与空间变化特性。因此,利用城市交通流的时空特性进行协同控制,能更好地制定相应的城市交通管控策略,进而合理、有效地管理交通流至最佳运行状态。

2 基于时空特性的交通协同控制

2.1 基于GA-WNN与最小二乘法的数据融合

采用文献[9]的相关系数法分析交通数据的时空相关程度,以相关系数绝对值大于0.8为标准选择关联路段进行协同控制计算。同时,利用GA-WNN算法处理路段的时间维度与关联路段的空间维度交通数据,得到最优时间、空间数据序列;运用最小二乘动态加权融合算法(简称“最小二乘算法”)将GA-WNN模型输出值进行融合,得到具有时空特性的交通数据进行区域协同控制。

设时间、空间维度的交通流数据为xi,以此作为WNN输入变量,得到隐含层和输出层计算结果[11]为:

(1)

其中,s(j)为第j个隐含层节点的输出值;sj为小波基函数,且s(x)=exp(-x2/2)cos(1.75x);bj、aj分别为平移因子、伸缩因子;λij、λjm分别为WNN输入层到隐含层、隐含层到输出层的连接权值;y(m)为第m个输出层节点的输出值;N、L分别为输出层、隐含层节点数;z为交通流数据维度。

采用GA初始化与最速下降法修正WNN的bj、aj、λij、λjm,得到GA-WNN输出的性能较好交通流数据后,以误差平方和最小为原则,根据动态误差大小对时空数据进行融合,得到协同路段的融合数据为:

(2)

其中,yt为t时段交通流数据时空融合值;ytr为第r个数据序列在t时段的GA-WNN输出值;wtr为ytr的融合权重;n为融合的时空数据序列个数。

设第r个交通流数据序列处理方差为σr,且σr=E[(Yt-ytr)2]。其中,t=t0-1,t0-2,…,t0-n0;Yt为t时段交通参数实测值。设n0=5,即选取该数据序列在t0时段的前5个时段处理结果方差值来确定融合权重,整理得到时空数据融合方差为:

(3)

令(3)式中wtr的偏导数为0,并取(3)式极小值,求得wtr=1/σr,则t时段融合权重与GA-WNN输出结果方差成反比。将wtr=1/σr代入(3)式,求得时空数据融合估计方差为:

(4)

由(4)式可知,采用最小二乘法得到的时空融合数据方差比单一时间、空间最优数据序列方差小,为协同控制提供的交通信息更可靠。

2.2 基于时空特性的交通协同控制模型

协同控制模型是通过分析交通流数据时空变化规律,利用离散化的时空融合数据在各个时段内建立时空饱和度与行程时间约束,通过对时空饱和度均值与方差的阈值限定来调控路网交通流分布,在保证交通不拥挤的前提下使路网行程时间最小。

考虑车辆驶入率与信号绿信比,以路段a(a=1,2,…,n1)在t时段的融合交通流量Va(t)与通行能力Ca计算路段时空饱和度ca(t)。同时,引入道路类别来标定不同路段的交通权重,采用时空饱和度在t时段的均值c(t)与方差S2(t)来限制与分配车流。因此,建立时空饱和度约束模型为:

J1=S2(t),

其中,φ、σ分别为时空饱和度均值、方差的阈值;δq为第q类路段(q取值为1、2、3,分别代表主干路、次干路及支路)饱和度的权重,δ1=0.5,δ2=0.3,δ3=0.2;ua(t)为路段a在t时段的车流驶入率;λa(t)为路段a在t时段的绿信比;Qa为路段a的饱和流量;n1为路段条数。

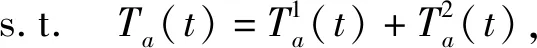
其中,ta为车辆在路段a上自由行驶时间;CI(t)为交叉口I在t时段的信号周期时长;yI(t)为交叉口I在t时段的时空流量比;α、β为阻滞系数,取值为α=0.15、β=4。

在时空交通数据基础上,计算得到S2(t)>σ或c(t)>φ时,以J1为第1目标进行优化,以J2为第2目标进行计算,得到路网交通参数;否则,直接以J2为目标,对协同区域进行交通控制与交通流分配。

2.3 基于GA-PSO的协同控制求解模型

采用GA优化的PSO算法来求解协同控制模型,通过引入交叉、变异等遗传操作[12],将个体更新转换为“粒子”在解空间上位置的移动,从而提高PSO全局搜索精度,达到控制协同区域时空饱和度,优化路网行程时间、道路节点周期及绿信比等交通参数的目的。

个体l按照自身移动速度、空间位置以及种群中适应度最优个体的空间位置更新其移动速度与位置信息,即

(7)

引入GA中选择、变异及交叉3种操作来求解协同控制模型。交叉是将2个个体的部分结构替换重组形成新个体,公式为:

(8)

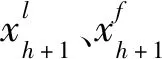
(9)

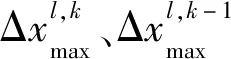
(10)

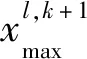
考虑交通流的时空特性,采用GA-PSO求解协同控制模型的流程如图2所示。在交通流数据时空变化特性分析基础上,采用时空融合数据在时空饱和度、行程时间约束下,利用GA-PSO算法以消除交通拥堵、保证路网行程时间最小为目标,对协同区域内各路段交通参数进行优化。

图2 基于GA-PSO与时空特性的协同控制流程

(1) 收集协同区域内的实测交通流数据,在时空相关性分析基础上,利用GA-WNN模型进行处理,采用最小二乘法进行动态加权融合,得到具有时空特性的融合交通流数据序列,以此作为协同控制模型的输入交通参数。

(2) 利用GA-PSO算法进行协同控制模型求解,并对粒子群的种群规模、迭代次数、c1、c2、r1、r2等参数进行初始化。

(3) 按照(5)式计算协同区域在t时段的时空饱和度均值c(t)与方差S2(t),建立时空饱和度约束模型。

(4) 判断c(t)与S2(t)范围,若S2(t)>σ或c(t)>φ不成立,则以目标函数J2计算适应度值,否则以目标函数J1、J2计算适应度值。

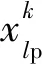
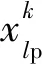
(7) 反复执行步骤(3)～步骤(6),直到满足迭代次数、误差精度与路网行程时间最小。

(8) 输出路网最小的行程时间T与最优信号周期CI、绿信比λa等交通参数。

3 算例分析

本文算例分析的道路网络拓扑结构如图3所示。图3中,A、B、C、D、E、F、G、H、L、M分别表示交叉口位置。该道路网主要包括黄山路、科学大道、香樟大道等主要干道,天智路与天柱路等次要干道,以及梦园路与天湖路等支路;路网中不同等级的道路相交形成了不同形式的丁字形、十字形等交叉口,用于模型验证具有代表性。该路网中多数路段与交叉口布设了微波、视频、地磁等车辆检测设备,交通流数据获取方便。由于梦园路、天柱路路段无交通检测器,为保证交通数据获取的准确性,选用黄山路与科学大道、黄山路与天智路、香樟大道与天湖路、科学大道与天湖路以及天智路与天湖路5个路口范围对协同控制模型进行分析。

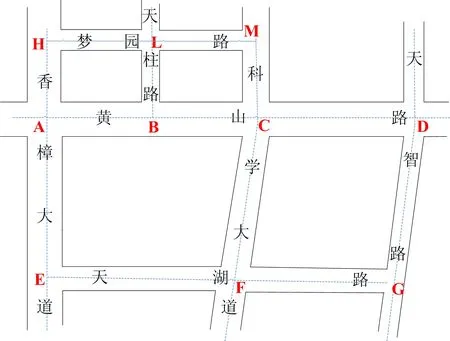
图3 算例路网拓扑结构

考虑到工作日交通流的相似性与交通数据的完整性,采用2016年7月4日—7月8日的交通流数据进行模型计算。为了反映样本数据采集的时效性,同时降低交通流波动对数据采集结果的影响,将交通数据进行5 min的时间间隔划分,即1 d有288组样本数据。对采集数据进行处理并核查,发现数据集中缺失了36条数据,占总数据的2.5%。为减少缺失值对协同控制的影响,将其他工作日同一时间采集数据的平均值填充至相应的数据缺失部分。

3.1 基于GA-WNN的时空特性数据处理

由于交通流具有时空相关性,单一时间、空间序列检测数据波动较大且精度不高,采用GA-WNN模型与最小二乘算法对各路段时间、空间维度的数据进行处理,得到时空特性交通流融合数据,以此作为区域交通协同控制输入变量。

以路段CD为例,首先利用相关系数法分析与相邻路段MC、BC、CF、DG交通流流量数据的相关性,得到的相关系数分别为0.958、0.937、0.846、0.753,即路段CD与路段MC、BC、CF的相关性较大,故空间数据考虑路段MC、BC、CF的影响;然后基于GA-WNN模型分别对路段CD的时间数据与空间数据进行处理,得到最优的时间、空间数据序列,且拟合精度分别为0.689、0.662,说明时间特性数据比空间特性数据好;最后,采用最小二乘算法对时间特性与空间特性的最优数据序列进行融合,得到路段CD时空相关的交通数据序列,且拟合精度为0.723,说明时空维度的数据最优。路段CD的时间维度、空间维度、时空维度的交通流量处理结果如图4所示。

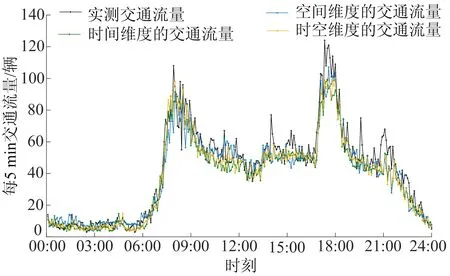
图4 路段CD的时空交通流量序列

由图4可知,处理后的时间维度交通流量消除了数据频繁抖动,使数据更加平稳;空间维度的交通流量虽然与实测值相比有一定偏差,但考虑了路网交通流的相互影响;时空维度的交通流量能够平稳地接近实测值,为区域协同控制的实施提供更可靠的基础数据。同时,为了说明时空维度的交通数据性能更好,选取平均绝对误差(mean absolute error,MAE)、平均相对误差(mean relative error,MRE)、均方误差(mean square error,MSE)以及均等系数(equality coefficient,EC)来量化分析数据精度[13],结果见表1所列。

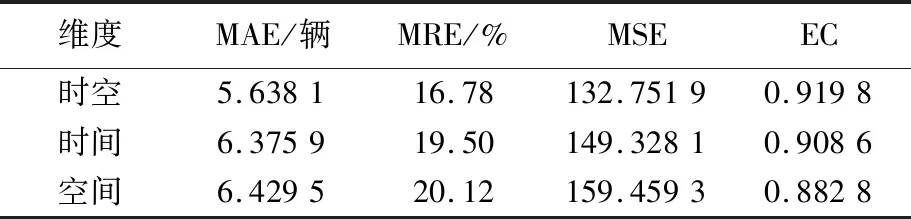
表1 路段CD的时空特性数据处理误差

由表1可知,考虑交通流时空相关性的融合数据明显优于单一时间、空间维度的数据序列;时空数据既考虑了交通流的相互影响,又协调了时间维度与空间维度的不同交通特性。为使协同控制数据包含时空信息,将路段CF、DG、FG、EF及其相关路段的交通数据也按上述步骤进行处理,得到各路段时空融合交通流量如图5所示。

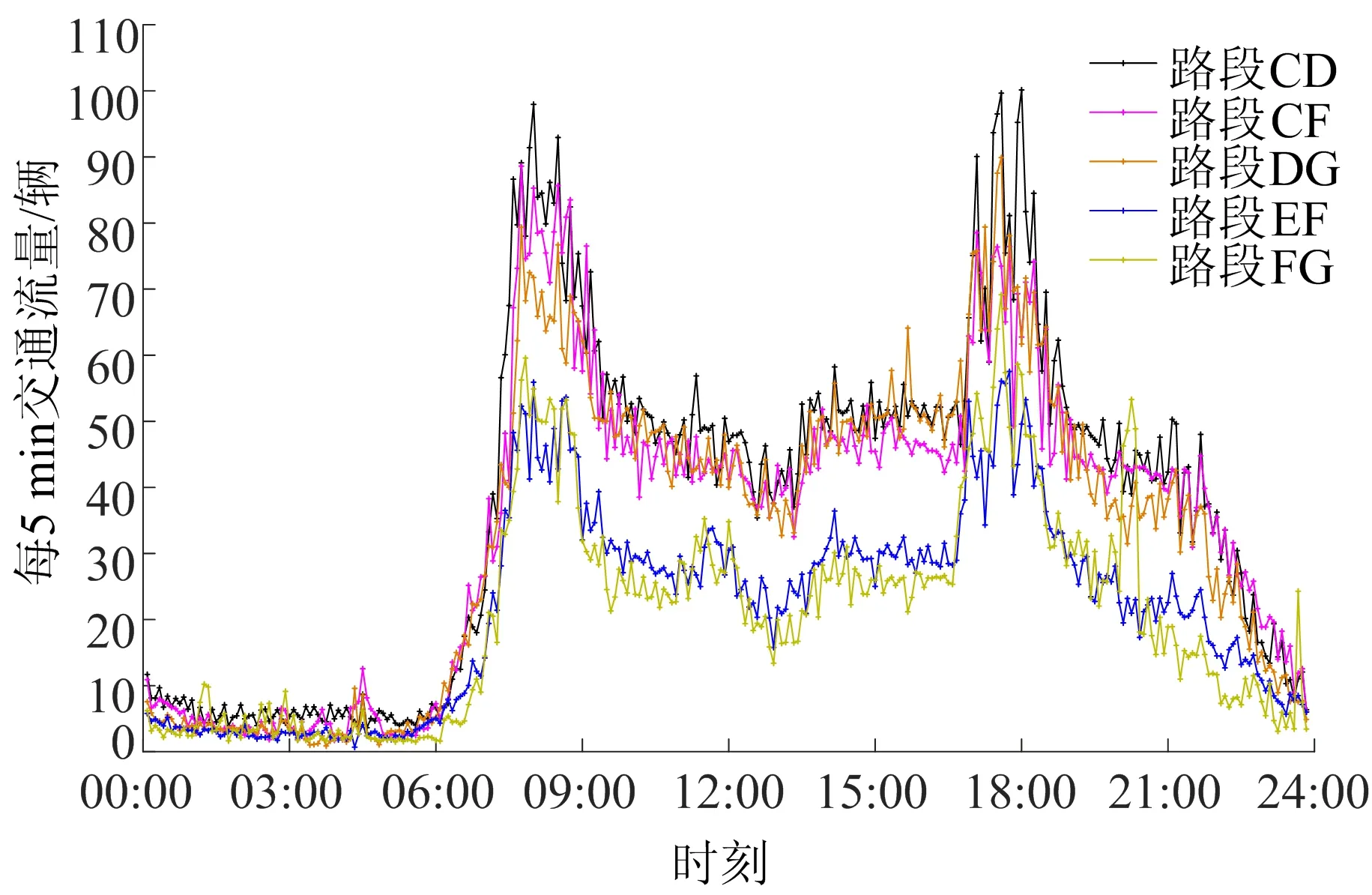
图5 各路段时空融合交通流量序列

时空融合交通流量既反映了断面交通状态在时间上的变化,又反映了路网交通流在空间上的分布,考虑了相关路段交通流的相互影响,具有更高的时空覆盖率及更综合的交通信息,能给路网协同控制提供更全面的基础交通数据。

3.2 基于GA-PSO的协同控制模型求解

3.2.1 数据初始化

为说明协同控制实施的有效性,选取平峰与晚高峰时段的小时交通数据进行协同模型验证。限于篇幅,选择路径E→F→C→D(路径1)、路径E→F→G→D(路径2)来分析协同控制实施效果。相关路段长度、自由行驶车速、基本通行能力(即1条车道上,单位路段长度所存在的车辆数[14])等参数统计见表2所列。

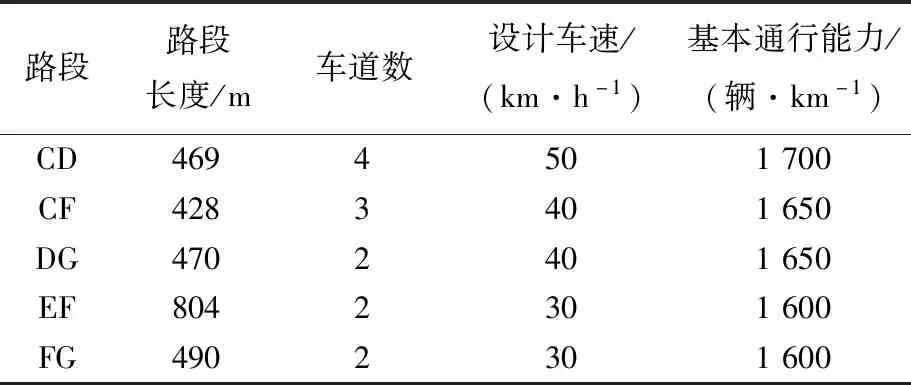
表2 各路段基本交通参数

根据3.1节中时空融合交通流量序列,计算路段CD、CF、DG、EF、FG在平峰、晚高峰的小时交通量,并按照(5)式计算路段时空饱和度ca(t)、路网时空饱和度均值c(t)以及饱和度方差S2(t),结果见表3所列。

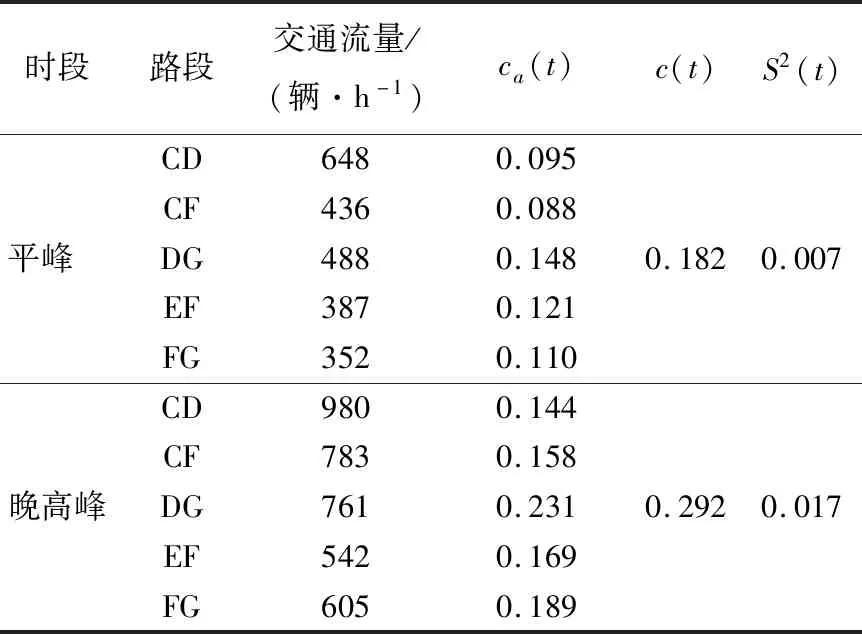
表3 2个时段初始交通参数

结合路网实际交通情况,设路段驶入率最大值为ua(t)=3辆/s,饱和度均值、方差最大值分别为φ=0.6、σ=0.05。基于2个时段内的初始交通参数,按照(5)式、(6)式以优化路网交通流分配与总行程时间为目标,利用GA-PSO算法来求解协同控制模型。

3.2.2 协同控制模型求解

利用GA-PSO算法求解协同控制模型时,设置种群规模为10,迭代次数为50。协同控制前、后,路网中交叉口C、D为四相位,E、G为二相位,F为三相位,各交叉口的信号周期CI(t)、与行驶路径有关的转向相位绿灯时间gI(t)(由绿信比换算而来)对比见表4所列。

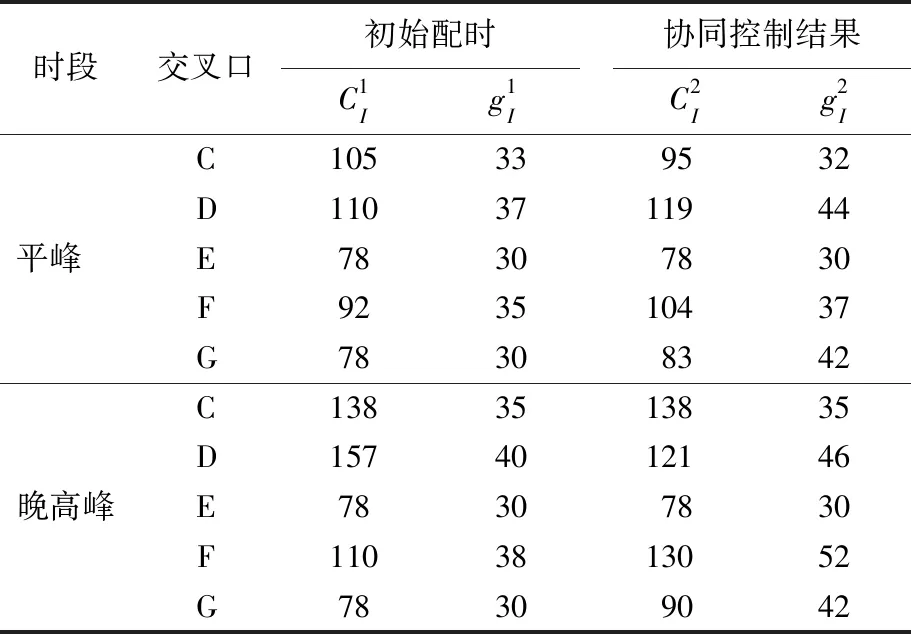
表4 协同控制前、后交叉口信号参数 s

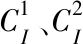
按照(10)式寻找路网行程时间最优解,得到平峰时段内路段CD、CF、DG、EF、FG交通流量分别为590、551、476、411、420 辆/h,晚高峰时段流量分别为881、857、641、576、568 辆/h;路径1在平峰与晚高峰的行程时间分别为267.7、302.3 s,路径2分别为239.6、278.4 s。

3.2.3 协同控制实施效果分析

为验证协同控制实施效果,利用VISSIM仿真软件对该小型路网的现状交通运行情况进行模拟,得到路径1在平峰与晚高峰时段的行程时间分别为309.7、345.4 s,路径2为291.8、327.1 s,将其与利用GA-PSO算法求解的协同控制后的行程时间作对比分析。考虑交通流时间与空间因素影响的区域协同控制,车辆在2个时段的行程时间与现状路网相比均有所减小。平峰时段,路径1的行程时间减小了17.9%,路径2的行程时间减小了10.1%;晚高峰时段,路径1的行程时间减小了12.5%,路径2的行程时间减小了14.9%。因此,时空特性下的交通协同控制取得了一定效果,在时间上车辆行程时间有所降低;在空间上路网交通流实现了合理分布,虽然部分路段交通流量有一定程度增加,但对整个路网而言,交通容量在协同前、后没有太大差异,并且提高了部分路段利用率。

4 结 论

通过对城市交通流的时间、空间与时空变化特性以及交通协同控制必要性的综合分析,考虑交通流的时空特性影响,利用GA-WNN模型分别对时间维度、空间维度的交通数据进行了处理,并利用最小二乘动态加权融合算法将时空数据进行融合,得到了最优时空融合交通流数据;以时空饱和度与行程时间为约束建立了协同控制模型,并采用GA-PSO算法进行模型求解;同时,利用VISSIM仿真软件对现状路网交通运行状况进行模拟,采用输出的行程时间来评价协同控制实施效果。算例分析结果表明,考虑交通流时空相关性的城市交通协同控制能有效减小行程时间,实现路网流量重新分配,从而能提高路网交通运行效率,达到缓解交通拥堵的目的。