一种数字图像相关非均匀位移精度优化方法

白鹏翔， 雷 冬， 朱飞鹏

（河海大学力学与材料学院，南京210098）

0 引 言

非接触测量技术在工业科研领域扮演着越来越重要的地位，光学测量方法是其中极为重要的一种技术。光学测量方法包括电子散斑干涉［1］、剪切散斑干涉［2］、全息干涉［3］、云纹干涉［4］等干涉技术，以其波长量级的灵敏度可用于微纳米级的测量，也包括数字图像相关［5］、栅线投影［6］、投影散斑［7］等非干涉技术，以其良好的适应性使得测量范围非常宽泛。

数字图像相关技术是一种基于数字图像处理和数值计算的非干涉变形测量方法，与其他测量方法相比，其优势明显：无需激光照明，无需隔振，对测量环境要求低，可用于较为恶劣的测量现场；实验设备及操作简单，实验过程仅需采集变形前后的数字图像；与不同的成像设备相结合，可以实现多个尺度下的变形测量，拥有广泛的测量范围。作为一种灵活有效而功能强大的变形测量手段，数字图像相关技术在工程实际应用中开始显示其实用性和优越性。

作为光学测量技术中适应性最强的测量技术之一，数字图像相关技术以其非接触、全场测量、设备简单、数据处理方便、测量范围涵盖了从宏观到微观等优点被广泛使用在生物医学、材料科学、土木交通、工业检测等各个领域中［8-12］，并且拥有广阔的应用前景。虽然拥有各种优势，与电阻应变测量技术相比数字图像相关技术在测量精度方面却存在较大的差距［13］，使得其在诸多方面的应用存在限制，如对于混凝土等脆性材料在开裂之前阶段的测量就具有较大误差。这种误差由多种因素造成，包括散斑大小及尺寸［14］、插值误差［15］、形状函数不匹配所造成的误差［16］等，其中形函数不匹配所造成的误差对非均匀变形尤其明显。

本文针对形状函数不匹配所造成的误差进行分析，提出一种简单易行的方法，不需要对相关匹配过程进行改动，最大程度地保留了现有程序的复用性，只对一阶形函数数字图像相关的位移测量结果进行简单的后处理，虽不能完全消除由于形状函数不匹配所造成的误差，但能够在很大程度上减小该误差，提高了数字图像相关的非均匀位移测量精度。使用基本函数和模拟数字图像对该方法进行检验，证明了该方法的有效性，以及可以作为数据处理中提高精度的一步后处理过程。

数字图像相关技术对于单个目标点的追踪所利用的信息并不局限于该点本身，其对于目标点的追踪本质上是对于目标子区的追踪，这样目标子区中散斑模式信息才能在运算中发挥作用。对于目标子区的比较判断是基于及数字图像相关中的一个基本概念——相关函数。相关函数是用于评价子区相似程度的一个函数，有学者对不同的相关函数进行比较分析并做出过评价，而本文所使用的相关函数为归一化最小平方距离相关函数，

式中：f和g分别为参考图像和变形图像；fm和gm分别是参考子区和变形子区的图像均值。该相关函数对于图像的整体明暗变化并不明显，因而对于照明条件并不理想条件下的散斑图像具有较好的兼容性，图像质量不佳时也能保证一定的测量精度。

形函数即位移模式是数字图像相关中用于描述图像子区基本变形的典型函数，是对物体变形的所作的一个基本假设。常用的形函数有一阶形函数和二阶形函数，其中一阶形函数运算简单计算量小，比较易于实现；二阶形函数相对复杂一些，在某些非均匀变形测量场合效果优于一阶形函数，但运算量比一阶形函数有明显的增大，因而在一般场合，一阶形函数的使用比二阶形函数相对广泛一些。

图1 所示即为一阶形函数的示意图，用数学公式表达如下：

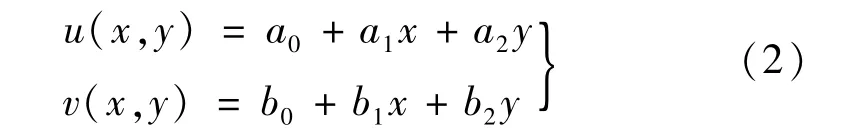
1 数字图像相关技术原理

数字图像相关技术是上世纪80 年代提出的一种非接触、全场光学测量手段。主要是在变形前、后对物体的被测表面拍摄数字图像，利用物体表面的自然纹理或人工在表面制造纹理特征作为物体表面信息的载体。对采集到的图像进行数字图像处理，当物体表面的点发生位置移动时，其移动信息就会在附近的散斑特征之中有所表现。通过相应的算法比较变形前、后物体表面的数字图像，对产生位移的点进行识别和追踪，获取其位移信息［5］。当对图像上所有目标点进行追踪时，就能够得到物体表面的位移场信息，通过对位移场信息进行差分等运算就可以获得表面的应变场信息。

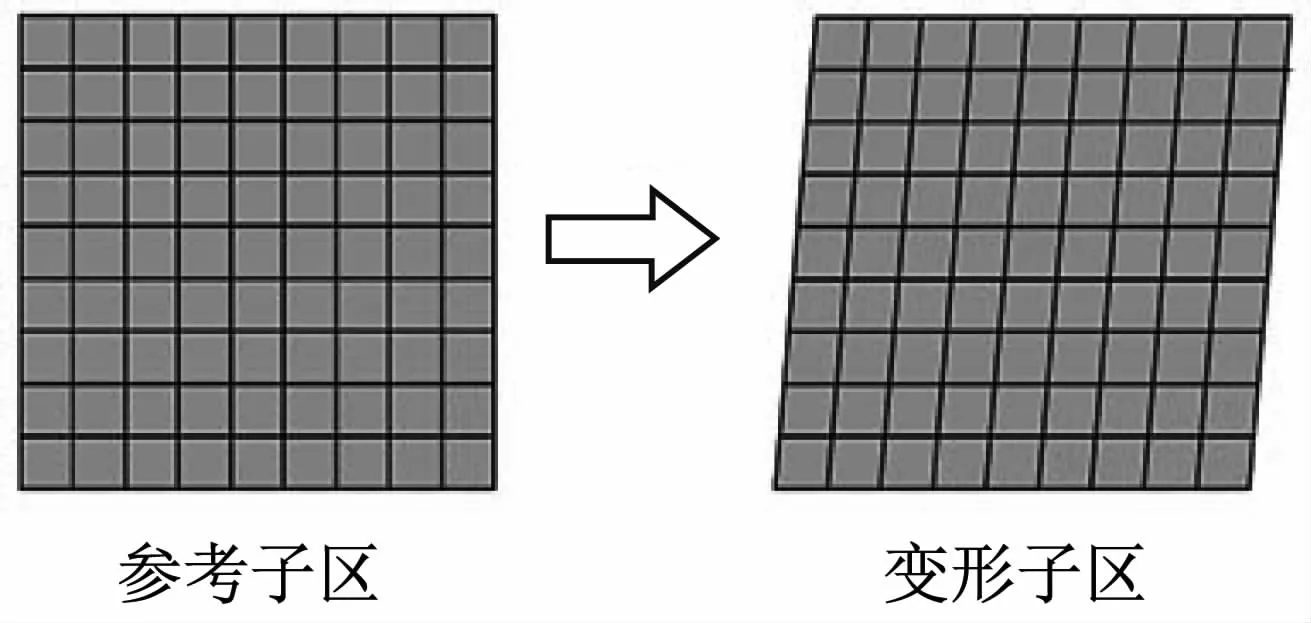
图1 一阶形函数示意图

图像子区遵循一阶变形形式，有6 个变形参数，包括2 个刚体位移参数和4 个位移梯度参数。

值得注意的是，不管是一阶还是二阶形函数，都是对物体表面变形所作的基本合理假设，意味着形函数都不可能完全表征物体表面的变形形式，只要采用了形函数，必然会引入由于形函数不匹配所造成的误差。图1 所示的一阶形函数，除均匀变形之外，物体表面的真实变形几乎不可能完全符合式（2）所描述的变形形式。

2 位移精度优化方法

2.1 误差来源分析

在数字图像相关技术中，关于形函数不匹配所造成的误差，已有学者对其做出了理论分析［16］，表明对于一阶形函数，位移计算结果相当于经过了一次滤波，该滤波的核如下式所示

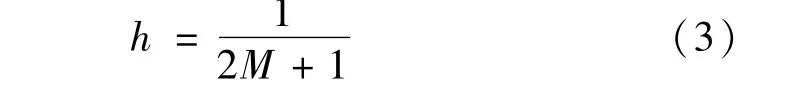
式中：h表示滤波的核；M表示图像计算子区的半模板尺寸。即位移计算结果等同于真实位移经过了一次均值滤波，而滤波尺寸即为图像子区的尺寸。而由于形函数不匹配所造成的误差本质上是该均值滤波所造成的平均效应，均值滤波从信号处理的角度来说是一种低通滤波器，不可避免会对位移信号的高频造成影响。对于均匀变形或者线性变形来说该滤波理论上不会造成额外的误差，反而会由于其平均效应使高频的随机误差得到一定程度的抑制，这也就是图像子区选择越大导致位移计算结果越平滑的原因。而对于非均匀变形来说情况就不同了，虽然随机噪声同样会得到抑制，但位移数据本身的高频分量同样被滤波器滤掉了，只有低频分量得以保留，造成位移数据显得越来越平缓，峰峰值必然会减小的情况。即如果能够存在一种方法对均值滤波后的数据进行恢复，也就能够抑制甚至消除位移模式不匹配所造成的误差了。

如图2 所示为一个简单函数的演示，原始数据为如下式所示的简单正弦函数，

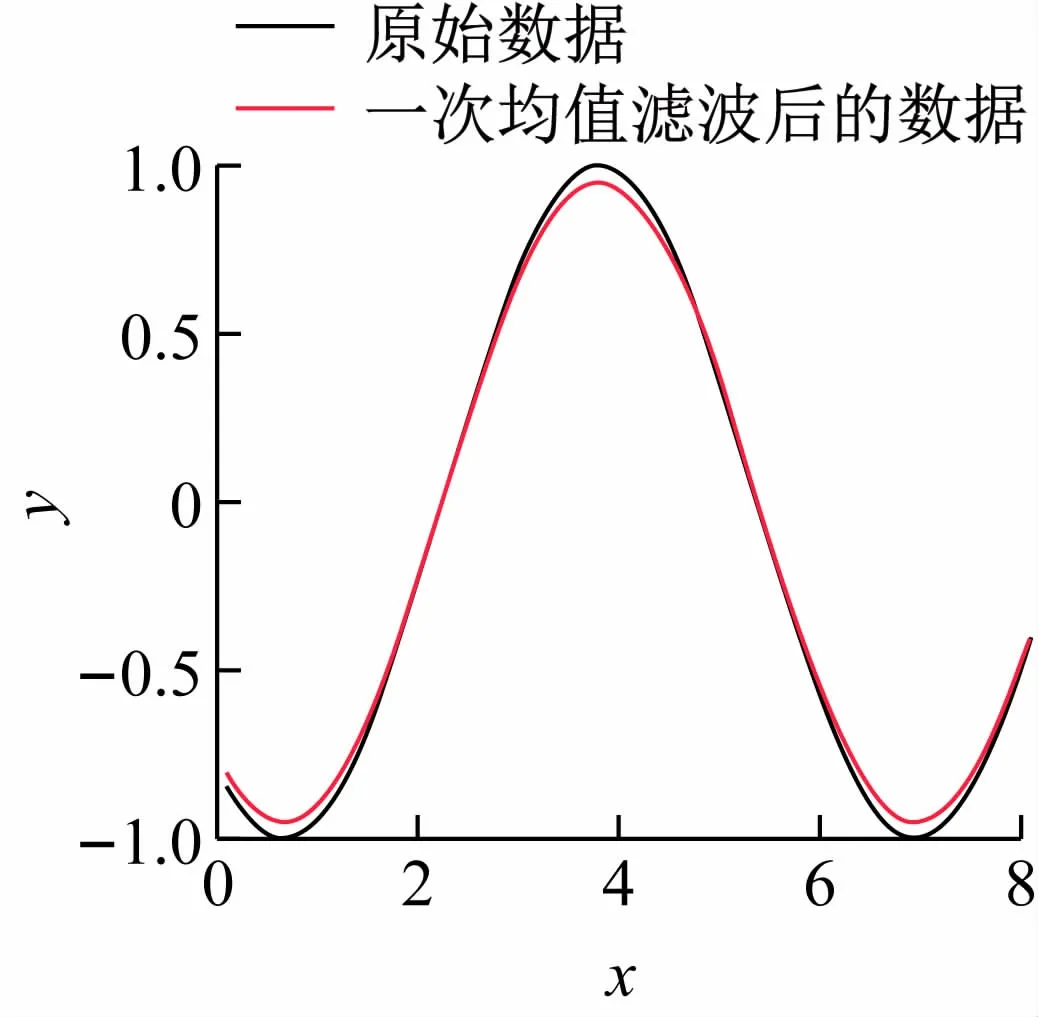
图2 原始数据与均值滤波后数据比较

经过一次均值滤波后的曲线与原曲线的对比，该次滤波窗口尺寸为1。可以看到原数据的峰峰值存在明显减小的情况，理论上正弦函数的最大值和最小值分别为1 和-1，滤波后上升峰和下降峰的峰值均有所减小，最大值和最小值分别减小到了0.95 和-0.95左右。

另外一个值得注意的现象是，均值滤波造成的误差是非均匀的。由图2 看出，在峰值处误差较大，在最大值处误差达到最大，而在非峰值处误差较小，某些点甚至不存在误差，误差的非均匀性也给误差的抑制带来了比较大的困难。

2.2 简单函数中的数据恢复

针对均值滤波所造成影响的规律，注意到如果对原始数据进行二次滤波（见图3），再与原始数据和一次滤波数据比较，则会发现规律则与一次滤波所造成的影响相类似，数据的峰峰值将进一步降低，原误差较小处的误差仍然较小，原峰值处的误差依然保持最大，实质上这也是由原数据本身的特性所决定。

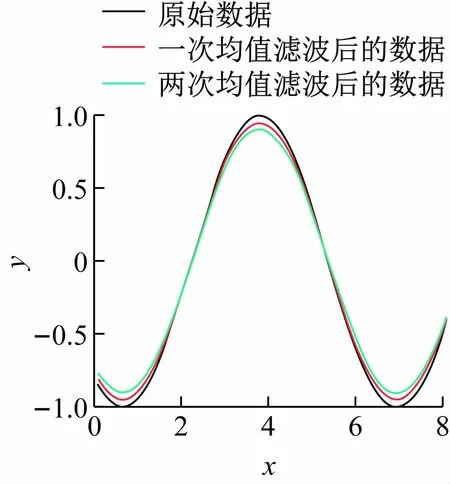
图3 原始数据和一次及两次均值滤波数据比较

因此，对两次均值滤波所造成的误差进行分析，如图4 所示一次滤波数据与原数据之差为红色曲线，两次滤波与一次滤波数据之差为绿色曲线。毫无疑问两次的数据之差必然存在一定的差别，然而从图4 可以看出，两次的数据差之间的区别并不大，即两次滤波对于数据曲线的平均效应是相似的，即一次滤波对原数据所造成的误差，与两次滤波对一次滤波曲线所造成的误差，两者之间有较强的类比性。所以，本文提出以后者作为前者的估计，即以第2 次滤波对曲线所造成的“削减”作用来估计或者替代第1 次滤波对曲线所造成的“削减”作用。

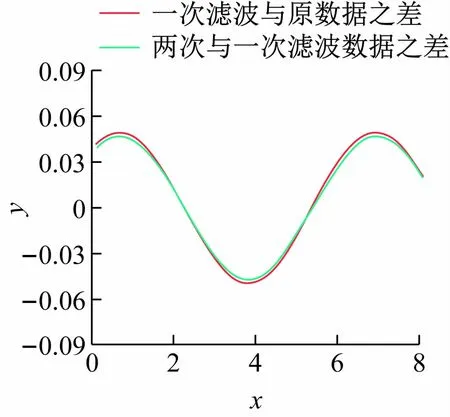
图4 两次滤波造成的数据之差

在实际操作层面上，原数据往往是未知而需要去求解的，能够获得的只有一次滤波后的数据，即图3 中的红色曲线，问题可以归结与在一次滤波数据的基础上，想办法获取原数据或原数据的估计，并尽量减小误差。所以本文提出的方法是：在一次滤波数据的基础上再进行一次均值滤波，以第2 次均值滤波所造成的误差作为第1 次滤波所造成误差的估计，将之叠加到一次滤波数据之上，作为原数据的估计，以此尽量减小由于均值滤波对原数据所造成的误差。

按照上述方法对图3 中数据进行恢复结果（见图5），包括原数据、一次滤波、二次滤波和本方法恢复的数据。原数据曲线为黑色，本方法恢复的数据为蓝色，由图5 局部放大图可以看出，黑色的原数据和蓝色的恢复数据大致重合，且与红色的一次滤波数据截然分开。为了更清晰地表明本方法的效果，将一次滤波数据、两次滤波数据、恢复数据与原数据之差进行比较，如图6 所示。可以看出，两次滤波数据的误差大致为一次滤波数据的2 倍，而恢复数据的误差基本在零附近徘徊，虽然并不完全等于0，但已明显比红色的一次滤波数据误差曲线小了一个数量级以上。

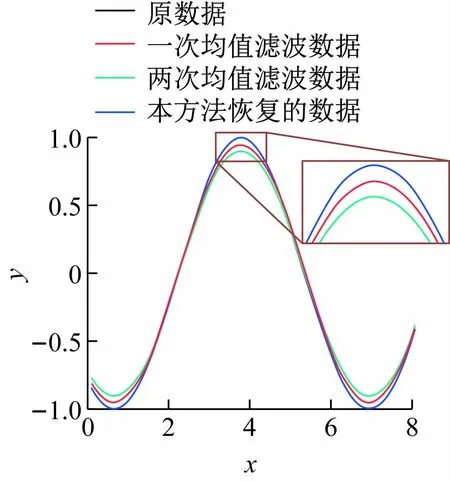
图5 原数据、一次、两次滤波、恢复数据对比

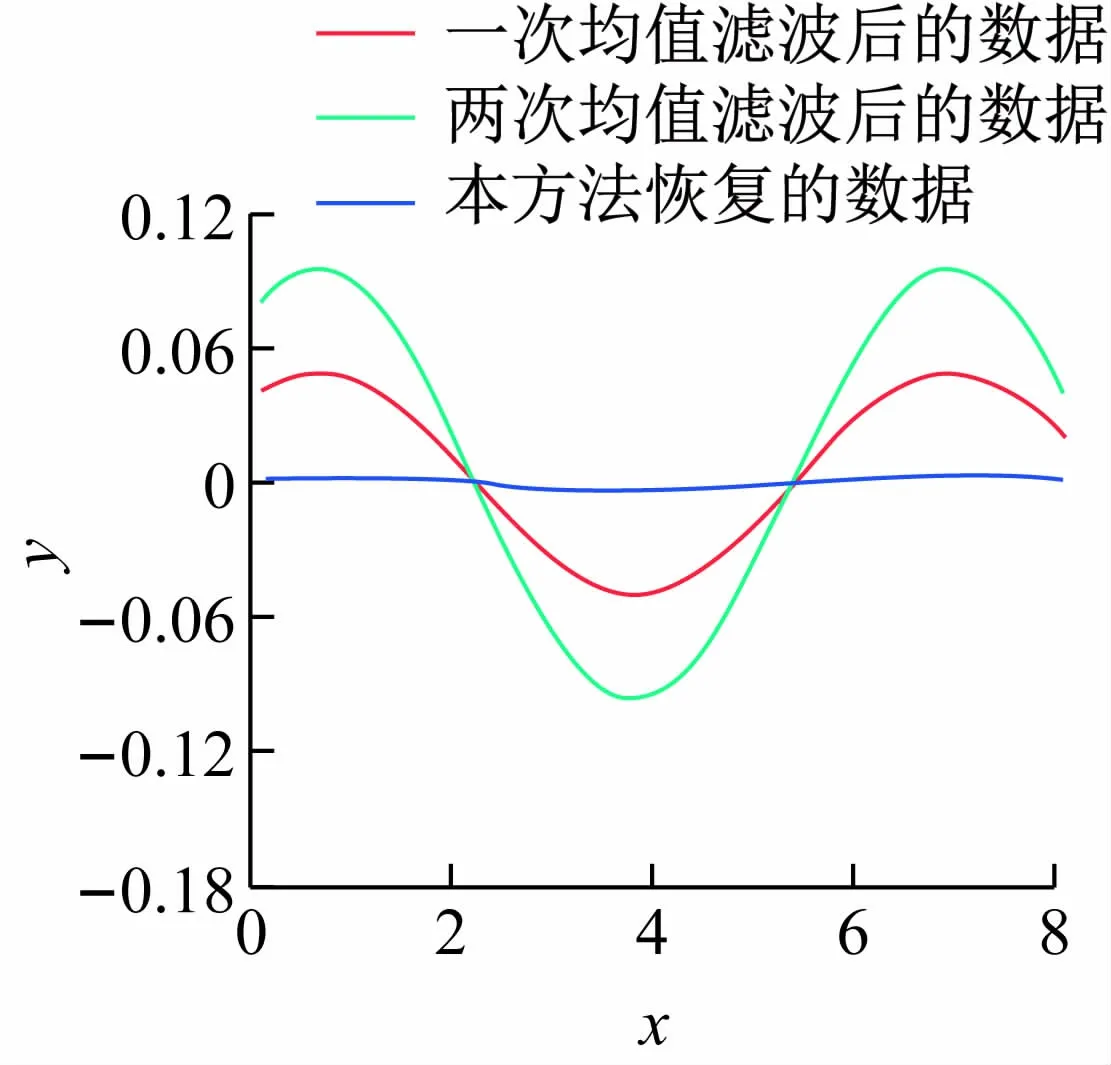
图6 一次、两次滤波、恢复数据误差对比

上述是对一种简单正弦函数的误差所作的分析，事实上本方法使用与各种复杂连续函数，如基本函数的混合，如下式所示

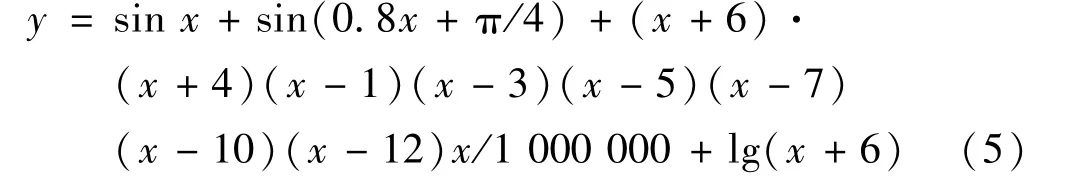
对该函数进行窗口尺寸为0.7 的均值滤波，并将本方法应用到一次均值滤波曲线上，对原始数据进行恢复（见图7、8）。

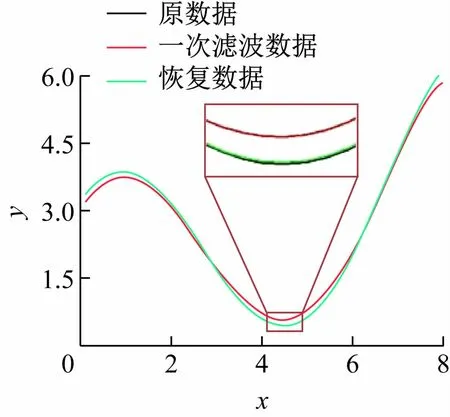
图7 混合函数的原数据、一次滤波和恢复数据

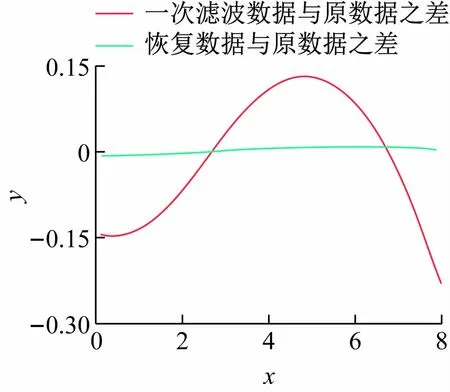
图8 混合函数的一次滤波和恢复数据的误差

2.3 模拟数字散斑图中位移数据的恢复

为了验证本方法对于数字图像相关技术不匹配位移模式造成误差抑制的有效性，以数值模拟的方式生成了两幅散斑图，如图9 所示。在两幅模拟图像中预设了非均匀位移如下式所示：

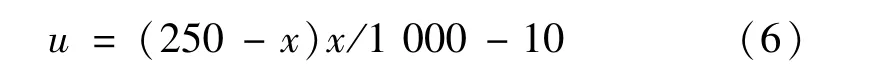
图9 模拟数字散斑图像

将模拟散斑图像用数字图像相关技术运算，获得横向位移场，如图10 中红色曲线所示，将本方法应用与所得横向位移场，得到恢复出的位移如图10 中绿色曲线所示。将两曲线与图10 中黑色曲线所代表的预设位移数据比较，看出恢复的位移数据更接近预设位移场数据。为了更清晰地对结果进行比较，将两者与预设数据的误差绘制曲线，如图11 所示。可以看到本方法恢复的位移场误差数值明显较小，可见由于形函数不匹配所造成的误差得到了很大程度的抑制。

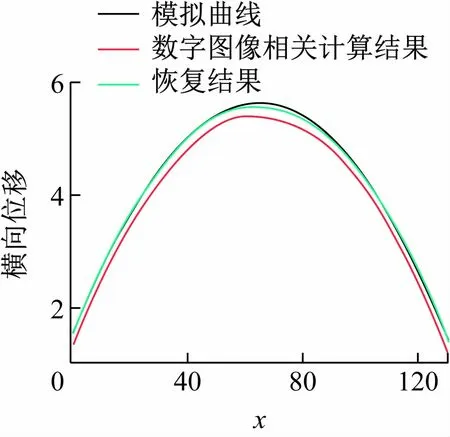
图10 模拟图像位移场的恢复结果

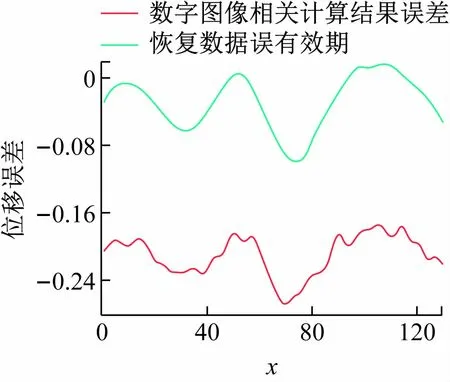
图11 模拟图像位移场误差比较

3 结 语

对数字图像相关技术中由于形函数不匹配所造成的误差进行了分析，确定了在一阶形函数下，该误差与一次均值滤波所造成的误差等同。发现了二次均值滤波的平滑效应与一次滤波类似，提出了以二次滤波的差值作为一次滤波的插值，用来对原位移数据进行恢复的方法。对简单正弦函数和混合函数进行了测试，结果表明该方法能够较好地对原数据进行恢复，误差减小了一个数量级以上。另外，还以数值方法生成了模拟散斑图，对模拟的散斑图进行数字图像相关运算，并将本方法应用于数字图像相关计算的位移数据，结果表明由于形函数不匹配所造成的误差在很大程度上被抑制了，取得了良好的效果。