基于布拉格光纤光栅的复合材料冲击信号特征分析

(南京航空航天大学 自动化学院， 南京 210016)

由于复合材料具有传统材料无可比拟的优越性能，在航空航天等工程领域得到了广泛的应用[1]。其中，复合材料层合板是存在于机身和机翼的典型结构，但其层间刚度较低，是一种对冲击载荷十分敏感的材料结构，而在其制造、运行过程中又十分容易受到冲击载荷。

冲击速度小于10 m·s-1的低速冲击[2]会造成复合材料层合板不可见的损伤,并在使用载荷下扩大，显著降低结构性能，具有很大的潜在危险性，因而，复合材料层合板的低速冲击特性在国内外得到了广泛的重视。郭飞等[3]利用冲击信号的小波包能量特征向量和相似度匹配算法，实现了对复合材料板材的低速冲击定位；陆观等通过分析冲击信号频谱峰值，实现了对复合材料低速冲击的能量等级划分[4]；通过对冲击信号进行WEMD(窗口经验模式)分解，确定信号能量特征集合，实现了对变厚度复合材料板的冲击能量分类[5]；SHRESTHA等[6]利用误差离群点算法对冲击信号进行分析，实现了机翼结构上的低速冲击定位;JANG等[7]利用高频光纤光栅解调系统研究了不同能量冲击信号的接触力情况，通过短时傅里叶变换分析了冲击信号与复合材料分层间的关系。

目前，复合材料层合板的低速冲击研究多集中在低速冲击能量与板材内部分层程度或冲击位置间的关系上，对复合材料层合板的低速低能量冲击的研究较少，而实际使用中的复合材料层合板，更多受到持续反复的低速低能量载荷冲击，其强度、刚度会不断受损直至材料失效[8]。因此，复合材料层合板低速低能量冲击的特性研究有利于实现对飞机复合材料层合板低速低能量冲击的长期监控，有利于减少飞机的地面维护人员的离线损伤检测工作，降低飞机的运行维护成本。

笔者通过分析复合材料层合板的低速低能量冲击过程，了解冲击信号的变化特性，分析了半正弦函数冲击信号模型在此变化特性下的频率幅值谱斜率变化规律；再将布拉格光纤光栅直接贴在复合材料层合板上，用来检测产生在另一侧的低速低能量冲击，通过分析布拉格光纤光栅的冲击传感信号，确认了通过检测冲击信号的频率幅值谱斜率来分析低速低能量冲击能级的可行性。

1 冲击信号的特性分析

1.1 复合材料层合板的冲击响应接触模型

目前，关于复合材料层合板的冲击响应接触问题还在研究当中，文献中有多种接触模型，尚没有完善的定论，其中，受认可度较高的OLSSON理论认为，复合材料层合板的接触响应受冲击物-板质量比的影响，而不是冲击速度的影响，使得不同的接触时间产生不同的复合材料层合板接触响应[9]。

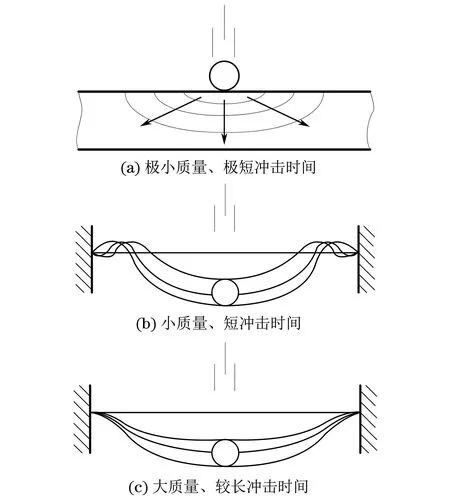
图1 复合材料层合板材受冲击时的接触模型

对一块确定的复合材料层合板材而言，当冲击物的质量非常小和冲击的接触时间非常短的时候，层合板的冲击响应主要为穿透厚度方向的应力波传递过程中产生的弹道效应，其接触模型如图1(a)所示；当冲击为通常意义的小质量、短接触时间时，层合板的冲击接触响应主要为剪切波、弯曲波作用的小质量响应，其接触模型如图1(b)所示；当冲击物的质量比板材质量大得多时，接触时间比剪切波、弯曲波传播到达板材边界所需的时间长得多时，层合板的冲击接触响应为准静态响应，其响应状态主要由板材使用结构的最低固有频率控制，其接触模型如图1(c)所示。

1.2 冲击信号模型的分析

在使用、维护过程中，飞机复合材料层合板经常遇到的轻微撞击、落体冲击等都属于低速冲击，其冲击时间一般在1 ms以上，可以给被冲击结构足够的时间来完成整体结构响应，因此不同质量的冲击物所造成的冲击响应模型主要是图1(b),(c)所示的两种或者两种的混合。又由于复合材料结构的特殊性，其基体材料主要用于黏接、支持、保护增强纤维和传递应力，被基体包围的增强纤维才是材料承受载荷作用的主要部分，增强纤维材料的强度性能通常比基体材料高出两个数量级，冲击载荷作用下的复合材料层合板通常是基体材料先失效形成分层，而增强纤维依然可以保持层合板的连续性。所以，在层合板承受持续反复的低速低能量冲击载荷过程中，一部分冲击动能变成了可恢复的弹性应变能，另一部分动能被材料吸收后，在基体、增强纤维中形成不同程度的失效损伤，损伤在多次冲击中不断累积，最终造成层合板的整体失效。这一过程中，在冲击响应模型分析中的结果就是，不同能量的低速低能量冲击响应的响应时间、最高响应幅值会不同，且和冲击能量密切相关；另一方面，在冲击信号模型的选择上，大多数研究都是将冲击信号和冲击引起的模态响应信号看做一个整体，对整个信号的频谱成分或选取信号特征值等参数进行分析，这方面的有效性得到了许多学者的研究证明，在离线检测中取得了较好的试验结果，但这种时间长度的选择不利于在线监测的实时性要求，故选择一个时间较短但能充分反映冲击特征的冲击信号模型和特征参数是十分必要的。

根据上述分析，忽略冲击引起的模态响应信号的影响，选取常用的半正弦函数作为冲击信号模型，如图4所示，研究冲击信号响应时间、最大响应幅值对冲击信号频率幅值谱分布的影响规律。信号模型的时间函数如式(1)所示。

(1)

式中:h0为测得的冲击信号峰值高度;T为信号的持续时间。

在采样频率为100 kHz、信号观察时间一定的情况下，分别改变信号模型的持续时间、信号峰值，观察信号频率幅值谱在500 Hz以内的变化情况，而准确描述频率幅值谱的分布规律较为困难，故以500 Hz内的频率幅值谱斜率作为变化特征值。在信号频率幅值0500 Hz的观察窗内，以观察窗区间的中点250 Hz将整个观察区分为0250 Hz,250500 Hz上下两个半区，取整个观察窗内的最高幅值极值点，再在与最高幅值极值点所处不同的另一个半区内选取最小信号幅值极值点，计算两点连线的斜率，以此斜率的绝对值作为观察窗内的频率幅值谱斜率。以通过应变所测的冲击信号为背景，通过文献资料及实验经验，选择接近实际冲击响应的时间长度，取整个观察信号时长为5 ms，分析模型冲击信号峰值(无单位)为600×10-6时，持续时间分别为1,1.25,1.5,1.75,1.8,2,2.25,2.5,2.75,3,3.25,3.5,3.75,4,4.25,4.5,4.75,4.9,5 ms时的500 Hz内频率幅值谱及其频率幅值谱斜率，以及模型冲击信号持续时间为1.5 ms，信号峰值为100×10-6,300×10-6,600×10-6,900×10-6,1 200×10-6,1 500×10-6时的500 Hz内频率幅值谱及其频率幅值谱斜率。

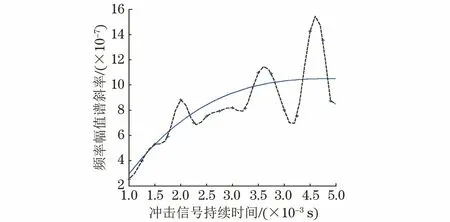
图2 信号持续时间对频率幅值谱斜率的影响

图3 信号峰值对频率幅值谱斜率的影响

图2为冲击信号峰值一定时，不同信号持续时间的频率幅值谱斜率，虚线为三次样条插值拟合曲线，实线为1,1.5,2,2.5,3,3.5,4,4.5, 4.9 ms离散点三次多项式拟合曲线，从拟合曲线可以看出，冲击信号峰值、信号观察时间一定时，频率幅值谱斜率总体随着信号持续时间的增加而增大，但增大过程是波动变化的，且信号增长的趋势变得平缓，波动幅值变大。从拟合曲线的趋势看，与纵轴的交点接近零点，这与持续时间趋近于零时，冲激函数信号的频谱斜率为零是吻合的。图3所示为信号持续时间、信号观察时间一定时，不同冲击信号峰值的频率幅值谱斜率，实线为一次拟合曲线，从拟合曲线可以看出，频率幅值谱斜率总体随着信号峰值的增大而线性增大，且增大速度较信号持续时间对频率幅值谱斜率的影响大。

当冲击物质量远大于复合材料层合板质量时，冲击持续时间与冲击物质量的平方根成正比[10]，而实际中的大质量冲击物通常是鸟类，其质量变化不大，冲击信号的频率幅值谱斜率主要受冲击信号峰值影响。当冲击物质量较小时，冲击信号的持续时间、峰值都会有较明显变化，冲击信号的频率幅值谱斜率受两者共同影响，低速低能量冲击多属于此类信号，上述分析表明，冲击信号峰值较信号持续时间对频率幅值谱斜率的影响大，而冲击持续时间与冲击物质量的平方根具有一定的关系，这会减轻低速低能量冲击中持续时间对频率幅值谱斜率的影响。综合上述分析，可知频率幅值谱斜率可以在一个较短的冲击信号时间序列里反映冲击信号的频率幅值谱分布情况，则通过计算观察窗中的频率幅值谱斜率来对低速低能量冲击进行能级分类具有可行性。

2 复合材料板的冲击测试

光纤布拉格光栅是一种光反射型传感器件，当一个宽带光源通过光纤布拉格光栅的栅区时，只有波长满足布拉格反射条件的光会被反射，其它波长的光都会透过光栅，物理量中的振动和应变等会使光纤布拉格光栅的有效折射率或光栅周期发生改变，从而使光纤光栅反射的特定波长的宽带光波发生偏移，最终实现对物理量振动和应变的测量。同时，光纤光栅具有和复合材料相容性好、质量小、体积小、抗电磁干扰、便于组网、传感一体等优点，因此，选用布拉格光纤光栅作为复合材料冲击检测的传感器。

冲击测试系统框图如图4所示，所用布拉格光纤光栅中心波长为1 550 nm，栅区长度为10 mm；复合材料板材为470 mm×270 mm×1 mm(长×宽×厚)的玻璃纤维环氧树脂板，环氧树脂板采用四边固支方式，板材边缘夹持宽度为10 mm，布拉格光纤光栅通过环氧树脂胶直接黏贴在复合材料板表面；光纤光栅解调仪为微光公司的SM130型解调仪，其解调频率为1 kHz。测试中使用额定能量为(1±0.5) J,直径为20 mm的半球形锤头的弹簧冲击锤产生冲击信号，冲击测试选择在复合材料板黏贴光栅的背面进行，冲击测试点如图4所示，其中，沿着光栅长度方向的测试点共有11个，距离光栅的中间点为0100 mm，两点间的间隔为10 mm;沿光栅周向方向的测试点共有16个，距离光栅中心点均为50 mm，测试角度为0°360°，两点间的间隔为22.5°。

图4 冲击测试试验系统框图

所获得的典型光纤光栅传感冲击信号如图5所示，冲击信号由冲击产生的主信号和谐振信号组成。进行频谱分析前，应先将中心波长信号转变为中心波长变化量信号，以去除直流分量，避免直流分量对频谱分析的影响。同时，冲击产生的谐振信号也会对信号的频谱产生影响，现采用模态分析计算出谐振频率，以最小谐振频率为频谱观察窗上限的方法来减小谐振信号对频谱分析的影响。通过ABAUQS仿真软件计算出的测试系统所用的四边固支复合板材的前10阶模态频率如表1所示，最小谐振频率为68 Hz，因此频谱分析中选择的观察窗为068 Hz。然后，采用1.2节所述的方法计算出冲击信号的频率幅值谱斜率，图6为沿着光栅长度方向各测试点的频率幅值谱及其频率幅值谱斜率，图7分别为沿着光栅周向方向各测试点的频率幅值谱及其频率幅值谱斜率。

图5 光纤光栅传感冲击信号

表1 四边固支复合板材的前10阶模态频率

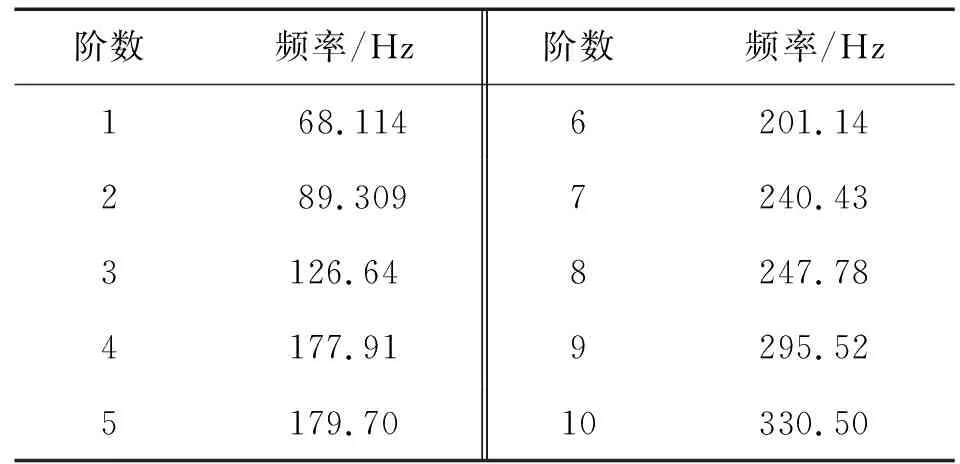
阶数频率/Hz阶数频率/Hz168.1146201.14289.3097240.433126.648247.784177.919295.525179.7010330.50

现对结果进行分析，图8为实际测试中光栅传感冲击信号频率幅值谱斜率随冲击距离的变化规律，虚线为三次样条插值拟合曲线，实线为三次多项式拟合曲线，从拟合曲线的趋势看，其结果与前述的理论分析结果相吻合，冲击信号的频率幅值谱斜率随着距离的增大呈下降趋势；在距离栅区中心小于40 mm的范围内，频率幅值谱斜率下降较明显，与理论分析中冲击信号持续时间在2 ms 以内的变化趋势相一致，说明在此距离内冲击信号的持续时间和峰值变化对频率幅值谱斜率的影响都比较大；在距离栅区中心4090 mm的范围内，冲击信号的频率幅值谱斜率波动变化较为平稳，在此距离内通过频率幅值谱斜率较难区分间距；当距离栅区中心大于90 mm时，冲击信号的频率幅值谱斜率相较于4090 mm的间距又开始出现了下降，但下降并不明显，此时冲击信号的幅值影响可能占据了更大的比例。图9为实际测试中光栅传感冲击信号频率幅值谱斜率随冲击位置所处光栅周向角度的变化规律，结果显示冲击信号频率幅值谱斜率也能大致反映出冲击所形成的花生状的应变变化区域，可用于评估冲击位置相对光栅的角度信息。

图6 光栅长度方向距离光栅中心0100 mm时的频率幅值谱及频率幅值谱斜率

3 结语

通过分析复合材料层合板的冲击响应接触模型，选择了合适的冲击信号模型，提出冲击信号频率幅值谱斜率为冲击信号的分析对象，对冲击持续时间、冲击信号峰值对冲击信号频率幅值谱斜率的影响进行了理论分析，再通过建立冲击测试实验系统进行了实际的冲击测试试验。试验结果表明，以冲击信号频率幅值谱斜率为特征分析参数可以有效地分析冲击距离产生的能量变化，评估冲击发生相对光纤光栅的位置信息。

图7 光栅周向0°337.5°的频率幅值谱及频率幅值谱斜率

图8 实测距离对冲击信号频率幅值谱斜率的影响

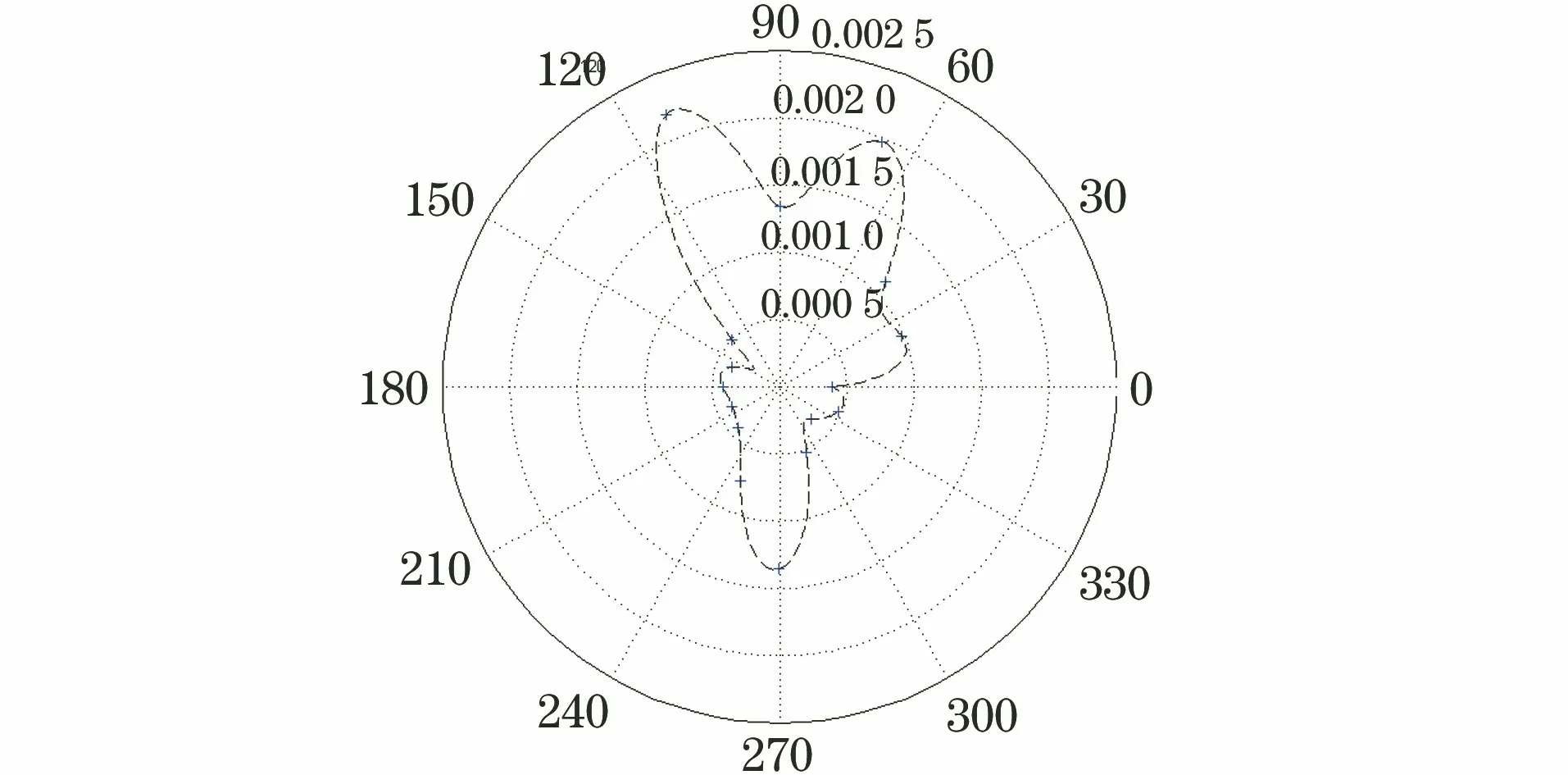
图9 实测冲击位置所处光栅周向角度对冲击信号频率幅值谱斜率的影响