轴编炭/炭复合材料组分材料的微细观热结构特性分析

朱昭君， 强洪夫， 王哲君

(1.火箭军工程大学 研究生院， 陕西 西安 710025； 2.火箭军工程大学 导弹工程学院， 陕西 西安 710025)

0 引言

轴编炭/炭(C/C)复合材料是固体火箭发动机喷管喉衬的首选材料，其工作环境处于高温、高速燃气流的冲刷和各相粒子的侵蚀，对复合材料热结构性能产生了巨大影响，同时内部组分材料产生了复杂的热应力、热应变，进一步影响喉衬结构的安全性[1-3]。轴编C/C复合材料的热导率和热膨胀系数是热结构特性的重要指标，较高热导率和较低热膨胀系数是材料设计的研究方向。在制造轴编C/C复合材料过程中，经过高温处理等工艺，使得组分材料纤维棒、纤维束、基体和界面发生了复杂的物理化学变化，同时微细观的结构特征通过影响组分材料而进一步影响材料的宏观热结构性能[4-6]。

目前，许多学者采用了实验仪器观测和数值分析方法对轴编C/C复合材料开展了微细观尺度的研究。在微细观形貌表征方面扫描电镜(SEM)使用的比较广泛，可以用来分析纤维束中纤维单丝的组织结构，以及基体和界面中的孔隙和裂纹缺陷[7-12]。许承海等[13-14]以及和永岗等[15]采用SEM表征了组分材料的微细观结构特征，纤维束内存在大量的纤维单丝，满足随机分布的特征。Rospars等[16]研究了热解炭基体中孔隙和裂纹对炭基体的热膨胀系数的影响，经过实验测定发现缺陷含量少的炭基体热膨胀系数较大。Sharma等[17]研究了炭纤维单丝的SEM微观形貌，认为微裂纹是由热氧化反应、湿热老化和疲劳共同作用引起的结果。高亚奇等[18]和Brandstetter等[19]采用特殊工艺预处理了轴编C/C复合材料，测试了材料在2 800 ℃温度载荷下的拉伸强度；通过SEM观测了组分材料纤维束，纤维单丝在制备过程中由于没有充分浸入沥青炭中，纤维单丝之间的间距较大。吴小军等[20-21]开展了轴编C/C复合材料的高温弯曲实验，结果表明，随着温度载荷的变化，轴向纤维棒方向的强度呈现先增大、后减小的趋势，弹性模量呈现减小的趋势。

由于编织结构的特殊性和加工工艺的复杂，单独完成组分材料纤维束热结构性能的测量非常困难，并且通常在复合材料数值分析过程中使用的是组分材料的原始性能。然而，组分材料在经过制备过程后，原始性能参数已经发生了变化，使用这些参数去预测复合材料的热导率和热膨胀系数就会出现较大的误差。Shi等[22]研究了轴编C/C复合材料的代表性体积单元(RVE)模型，结合有限元方法计算了材料在不同石墨化处理温度和界面刚度下复合材料热应力的分布。高亚奇[23]分析了轴编C/C复合材料的微观特征对热膨胀系数的影响，热膨胀系数表现出各向异性的原因是微观缺陷在受热载荷过程中吸收能量的原因造成的。Wei等[24-25]和Wongsto等[26]从组分元素炭的性质和石墨化工艺分析了对热结构参数的影响，经过石墨化处理后试件的热传导率和热膨胀系数会增大，主要原因是基本组成元素炭的晶体结构得到了重组的改善而造成的。Farhan等[27]测定了复合材料沿轴向纤维棒方向以及径向纤维束方向的热膨胀系数并计算了材料不同方向的热导率，结果显示径向的热膨胀系数高于轴向的热膨胀系数。Zhai等[28]基于复合材料的RVE模型，完成了热结构耦合下的力学性能预测，研究了编织角和温度载荷对力学性能的影响，完成了复合材料的3点弯曲实验，预测结果和实验结果比较接近。Kumar等[29]研究了轴编C/C复合材料热膨胀系数、扩散率和比热容随温度的变化规律，得出热膨胀系数沿轴向纤维棒方向和径向纤维束方向数值不同的结论。顾靖伟等[30]提出了预报轴编C/C复合材料热膨胀系数的能量法，研究了复合材料编织参数对复合材料热膨胀系数的影响。封伟强[31]通过SEM表征了组分材料纤维束的微细观形貌，建立了纤维束的RVE模型，在施加周期性边界条件基础上计算了组分材料的刚度矩阵。

总结这些研究成果，在实验方面多是对轴编C/C复合材料不同方向的热膨胀系数和热导率的测量，以及常温和高温实验条件下复合材料拉伸、压缩和剪切的力学性能研究。数值模拟多是在复合材料RVE基础上完成常温刚度性能的数值模拟，针对轴编C/C复合材料特有的微细观结构特征对复合材料等效热结构参数的预测研究开展的较少。因此，本文首先开展轴编C/C复合材料微细观形貌的表征实验，推导两种单胞模型的温度周期性边界条件表达式，完成组分材料纤维束微细观RVE模型的建立；其次在均匀化理论的基础上用Python语言编写程序实现等效热结构参数预测方法的应用，计算纤维束RVE模型等效热结构参数；最后提出一种等效热结构参数预测方法和轴编C/C复合材料微细观热结构性能的多尺度研究方法。

1 微细观特征表征实验

1.1 实验方法及设备

轴编C/C复合材料的微细观结构特征主要体现在微观层次上的组分材料纤维束内部的纤维单丝和单丝周围的基体，以及基体和界面单元内部的孔隙和裂纹。细观层次上指组分材料纤维棒、纤维束与复合材料内基体以及界面单元。本文重点研究组分材料纤维束的热结构性能。如图1所示为轴编C/C复合材料的观测试样，纤维棒、纤维束与基体在图中所示。图2是轴编C/C复合材料的增强体纤维棒和纤维束，纤维束由0°、60°、120°等3个方向构成，纤维束依次穿过纤维棒形成层间增高。

图1 复合材料观测试样Fig.1 Experimental sample

图2 增强体示意图Fig.2 Schematic diagram of reinforcement

1.2 实验结果及分析

实验通过SEM观测复合材料和组分材料纤维束的微细观形貌。图3中：a代表复合材料的组分材料轴向纤维棒，纤维棒相互之间是正三角形排列，纤维棒的横截面可以等效为圆形；相邻纤维棒之间是基体,如图3中b所示，从图3中可见基体内存在大量的孔隙，呈现随机分布的特征。图3中c所示为60°方向的纤维束，纤维束之间相互平行，依次穿过纤维棒之间的通道，在纤维束中可见存在一些裂纹。

图3 轴编C/C复合材料轴向显微形貌(a-纤维棒；b-基体；c-纤维束；放大10倍)Fig.3 Axial microscopic morphology of 4D carbon/carbon composites(a-fiber rod; b-matrix; c-fiber bundle; 10×)

图4是纤维束中纤维单丝微观形貌，从中可知纤维单丝在纤维束增强体内是随机任意分布，纤维单丝周围由基体组织包围，纤维单丝之间较紧密一些。图5是纤维单丝的微观表征形貌，从中可以观测到纤维单丝的表面形态，是不规则的石墨微晶片层结构。纤维单丝的截面近似为圆形，内部的成分石墨由中心向外形成条纹，纤维单丝的外部是基体炭。

图4 纤维束显微形貌(放大1 000倍)Fig.4 Microscopic morphology of fiber bundle (1 000×)

图5 纤维单丝显微形貌(放大3 000倍)Fig.5 Microscopic morphology of fiber monofilament (3 000×)

2 等效热结构参数的计算

通过组分材料纤维束的微细观表征实验可知纤维单丝在纤维束内为随机性分布，每根单丝的横截面可以近似为直径相同的圆形。因此，在纤维束微细观形貌观测实验的基础上，可以为纤维束RVE模型的建立提供直观依据。本文提出在微细观尺度建立纤维束的RVE计算模型，来分析纤维束的热结构性能，提出纤维束微细观热结构性能的研究方法。

2.1 温度和位移周期性边界条件

Xia等[32]提出了周期性边界条件，同时结合均匀性理论以及复合材料的热传导规律，可以得到复合材料的等效热结构参数。文献[32]中已经论述了立方体单胞和正六棱柱单胞的位移周期性边界条件，此处不再赘述。现推导两类单胞模型的温度周期性边界条件表达式，图6为立方体单胞模型。图6中：单胞的长、宽、高分别为2a、2b、2c；角点分别定义为1～8；棱边可以按照平行于x轴、y轴、z轴3个坐标轴分为3组，分别为平行于z轴的组合(l12,l34,l78,l56)，平行于y轴的组合(l15,l48,l37,l26)，平行于x轴的组合(l14,l58,l67,l23).

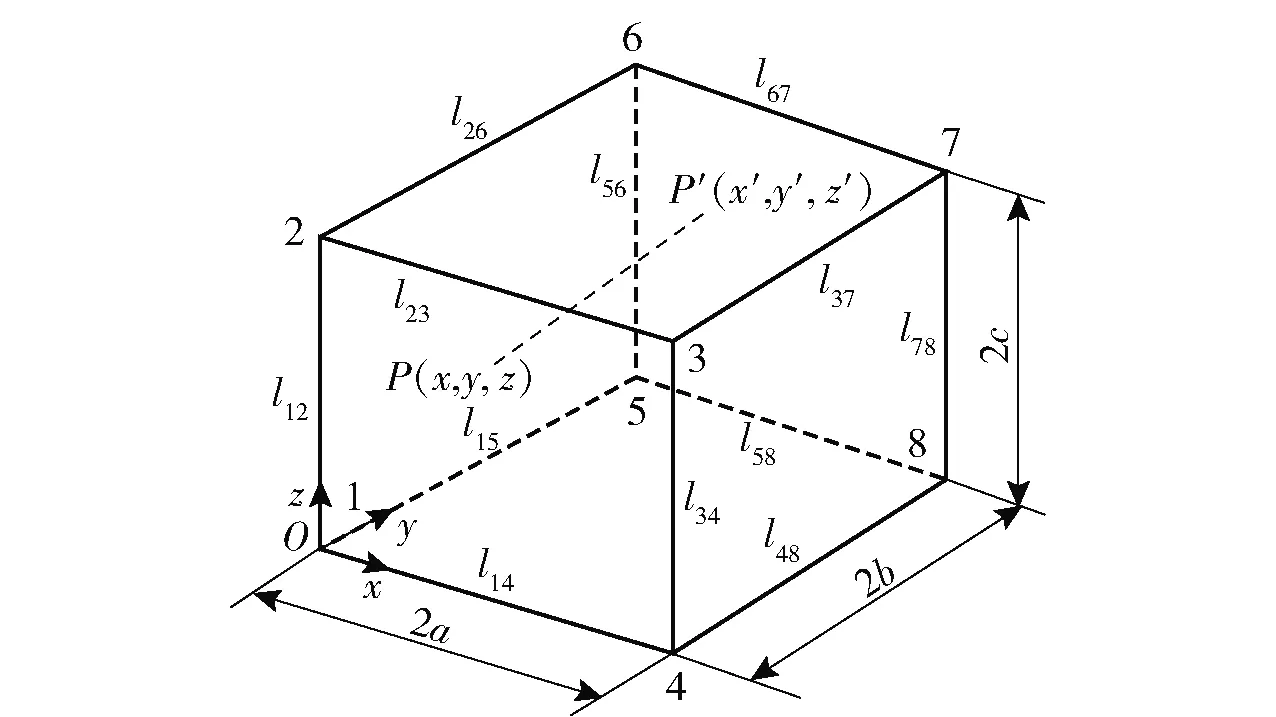
图6 立方体单胞模型Fig.6 Definitions of cubic unit cell faces, edges and nodes

施加在单胞的温度梯度表示为

(1)

(2)

式中：括号内的变量Tx=a、Ty=b和Tz=c，以及括号外的|y,z、|x,z和|y,x下标分别表示单胞相应面、边和角点位置的温度，下文中其他周期性温度边界条件表达式中变量的下标含义也是同样。立方体的棱边被相应两个面共享，角点被相应3条棱边共享，所以对于棱边和角点应建立各自不同的温度周期性边界条件。因此，建立棱边的温度周期性边界条件为

(3)

以角点1为参考点，建立角点的温度周期性边界条件为

(4)

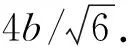
(5)

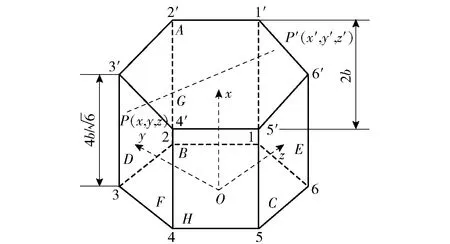
图7 正六棱柱单胞Fig.7 Definitions of hexagonal unit cell faces, edges and nodes

因此，建立的4组对应面的温度周期性边界条件为

(6)

同理，建立的棱边温度周期性边界条件为

(7)

建立的角点温度周期性边界条件为

(8)

2.2 热物理性能研究

轴编C/C复合材料是一种各向异性材料，导热定律为

(9)

边界的平均热流为

(10)

(11)

式中：Ki为单胞沿坐标轴方向的热导率；∂T/∂xi为单胞不同方向的温度梯度；Qi为单胞不同方向的热流；qi为单胞不同方向的平均热流；Si为单胞模型热流输出面的面积；ai为单胞边长。利用(9)式～(11)式可以求出热传导系数：

(12)

同理，对单胞模型进行稳态热分析时，在初始温度应变的作用下，应力的更新为

σ=C(χ+I)=C(χ-κΔT)，

(13)

式中：σ为单胞应力矩阵；χ为细观尺度的位移；C为弹性张量；κ为温度应力矩阵；I为温度变化引起的温度应变矩阵，计算式为

I=ΔT[αx,αy,αz,0,0,0]T，

(14)

αx,αy,αz为复合材料沿3个坐标轴方向的热膨胀系数。因此，在施加载荷ΔT取1的条件下，同时施加位移的周期性边界条件，计算得出3个方向的热膨胀系数的值等于单胞相应的等效应变值。

在建立组分材料的RVE模型上，分别施加位移和温度周期性边界条件可以得到等效刚度值、等效热膨胀系数和等效热导率。在本文微细观有限元分析中，周期性边界条件的施加，通过在单胞模型的平行相对面、边和角点的相应网格节点实现。因此，对于上述过程的实现，需要Python语言编写程序实现等效热结构参数的计算，进而在Abaqus软件中调用运行计算。

为验证本文提出的计算等效热结构参数方法的正确性，现以表1中基体材料的参数为基础，材料参数来自于文献[33-35]，建立具有各项同性属性性质的计算模型进行分析计算。计算结果如图8所示。

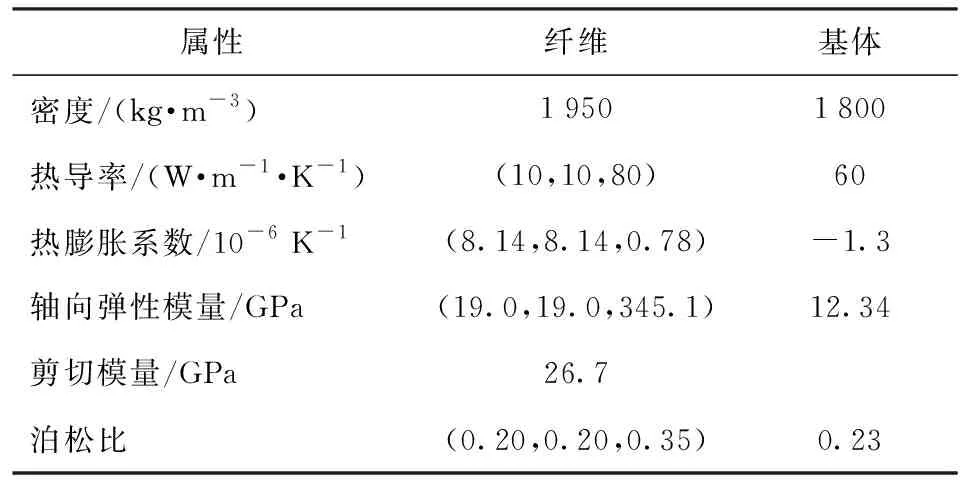
表1 纤维和基体材料参数[33-35]

图8 均匀体RVE模型分析结果Fig.8 Predicted result of homogeneous RVE

如图8(a)为预测计算得到的等效热结构参数值，其中弹性模量为E1=E2=E3(E1为轴向弹性模量，E2、E3为径向弹性模量)，泊松比ν12=ν13=ν23(ν12、ν13为径向泊松比，ν23为轴向泊松比)，热膨胀系数α1=α2=α3(α1为轴向热膨胀系数，α2、α3为径向热膨胀系数)。由此可知，预测结果等于表1中基体材料属性值，验证了材料属性各向同性性质的结论。如图8(b)中的预测应变值等于材料的热膨胀系数，这是由于在施加位移周期性边界条件后，温度载荷施加为1的条件下，应变值等于输入的膨胀系数值，从(14)式也可以计算得出，因此进一步验证了本文提出的计算等效热结构参数方法的正确性。

3 微细观热结构特性分析

喉衬用轴编C/C复合材料在热载荷作用下的热应变是组分材料综合作用的结果。组分材料纤维束的微观尺度热结构特性分析以均匀化理论为基础，在RVE模型的基础上施加周期性边界条件，利用预测等效热结构参数的方法完成组分材料纤维束等效热性能参数的确定。在纤维束微细观形貌表征实验基础上，可以建立的RVE模型包括常规RVE和任意分布RVE.

3.1 纤维束常规RVE模型分析

按照纤维单丝在纤维束内的分布情况如图9所示，可以建立两种常见类型的RVE模型，分别为图10(a)和图10(b)所示。这两种RVE模型具有相对简单的几何形状，现分析不同纤维体积含量下RVE模型的等效热结构参数。

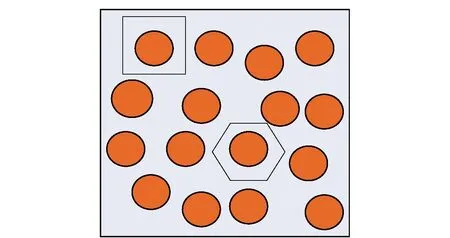
图9 纤维单丝分布示意图Fig.9 Fiber monofilament distribution in fiber bundle

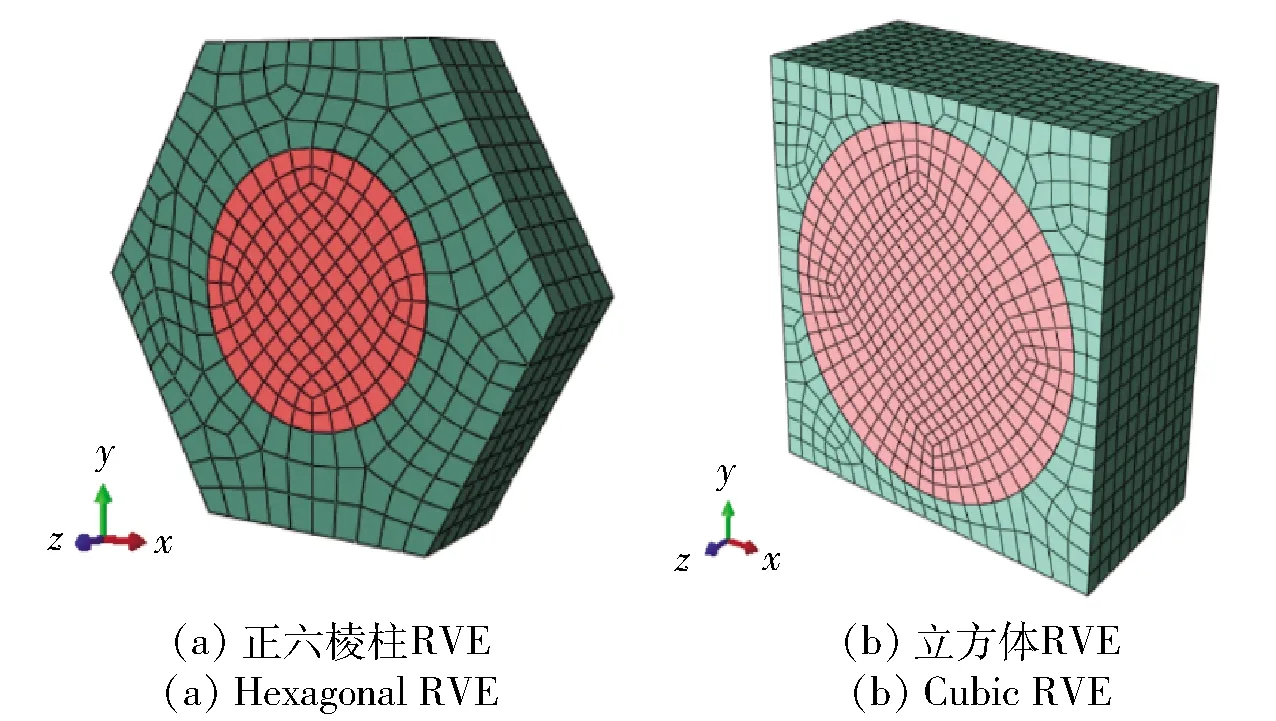
图10 常规纤维束RVE示意图Fig.10 Schematic diagram of normal fiber bundle RVE

根据复合材料的混合法则，复合材料等效刚度和等效热结构参数都可以根据(15)式计算。按照混合法则计算出的值是轴向刚度上限值以及横向刚度的下限值、轴向和径向热膨胀系数的最大值、热导率的最大值以及最小值，在这里可以作为一种参考值。(15)式为

(15)

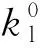
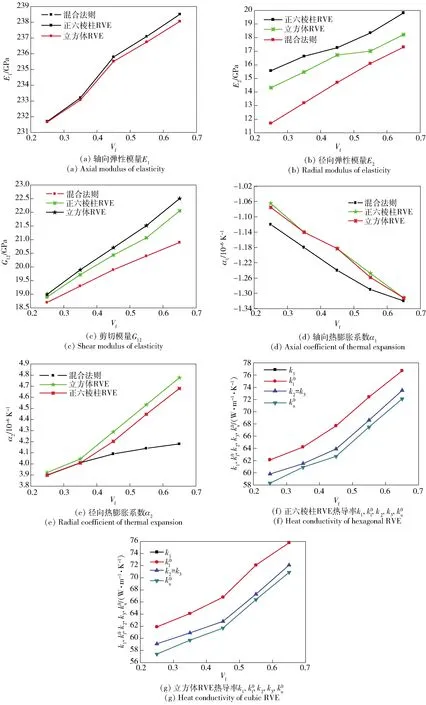
图11 等效热结构参数与混合法则计算结果对比情况Fig.11 Comparison of predicted and calculated effective thermo-structural parameters

由图11的分析结果可知，随着纤维体积含量的增加，采用正六棱柱RVE模型和立方体RVE模型计算的等效刚度系数和等效热结构参数的变化趋势与混合法则计算结果变化趋势一致。如图11(f)和图11(g)中纤维单丝方向的k1等效热导率近似线性增加，与采用混合法则计算的热导率的上限值相同，径向的k2=k3等效热导率变化趋势与混合法则计算的热导率下限值变化趋势一致。由于混合法则只是对参数的上限或者下限的一个估计值，RVE预测结果和混合法则的分析结果之间存在一些差异是合理的。

3.2 任意分布纤维束RVE模型

为建立纤维束的随机RVE模型,对单根纤维分布应用随机移动函数，使每根纤维沿任意方向移动到任意距离，满足任意两个纤维相互不发生干涉，直到设定区域的纤维体积分数等于纤维束纤维单丝体积分数的设定值。应用Python语言编程实现上述过程，如图12为生成的满足纤维单丝随机分布的随机RVE示意图。

图12 移动纤维法生成随机RVEFig.12 Random RVE of fiber bundle created by mobile fiber method

为了分析对比采用正六棱柱RVE、立方体RVE和随机RVE的预测精度，设定这里所有RVE的纤维体积含量选择为60%，炭纤维和基体的材料性能如表1所示。结果列于表2，其中实验数据来自于文献[22,36]。如图13(a)和图13(b)为生成的两个随机RVE计算模型，厚度设定为单位厚度值。

从表2的预测结果可知，等效刚度值以及等效热膨胀数值在x轴和y轴两个坐标轴方向近似相同，证明了RVE模型在Oxy平面满足横向各向同性的性质。其中正六棱柱RVE模型在横向各向同性预测值误差最小。3类RVE模型预测值大于实验值的原因是由于轴编C/C复合材料是一种易脆性材料，在实验过程中对纤维束的取样容易造成破坏，同时在材料加工过程中，温度会影响纤维单丝和炭基体的性能参数[11]，因此预测值大于实验值。

表2 纤维束不同RVE模型计算结果

图13 随机RVE模型Fig.13 Random RVEs of fiber bundle

如图14所示为立方体RVE模型施加纤维棒方向载荷下的热流密度(HFL)分布图，从中可知最大HFL值为11.71 W/m2，出现在纤维处，表明纤维的热导率大于基体。RVE模型的温度场(NT11)分布与基体NT11分布相同，验证了RVE模型温度场实现了周期性分布，验证了预测等效热结构参数方法的正确性。

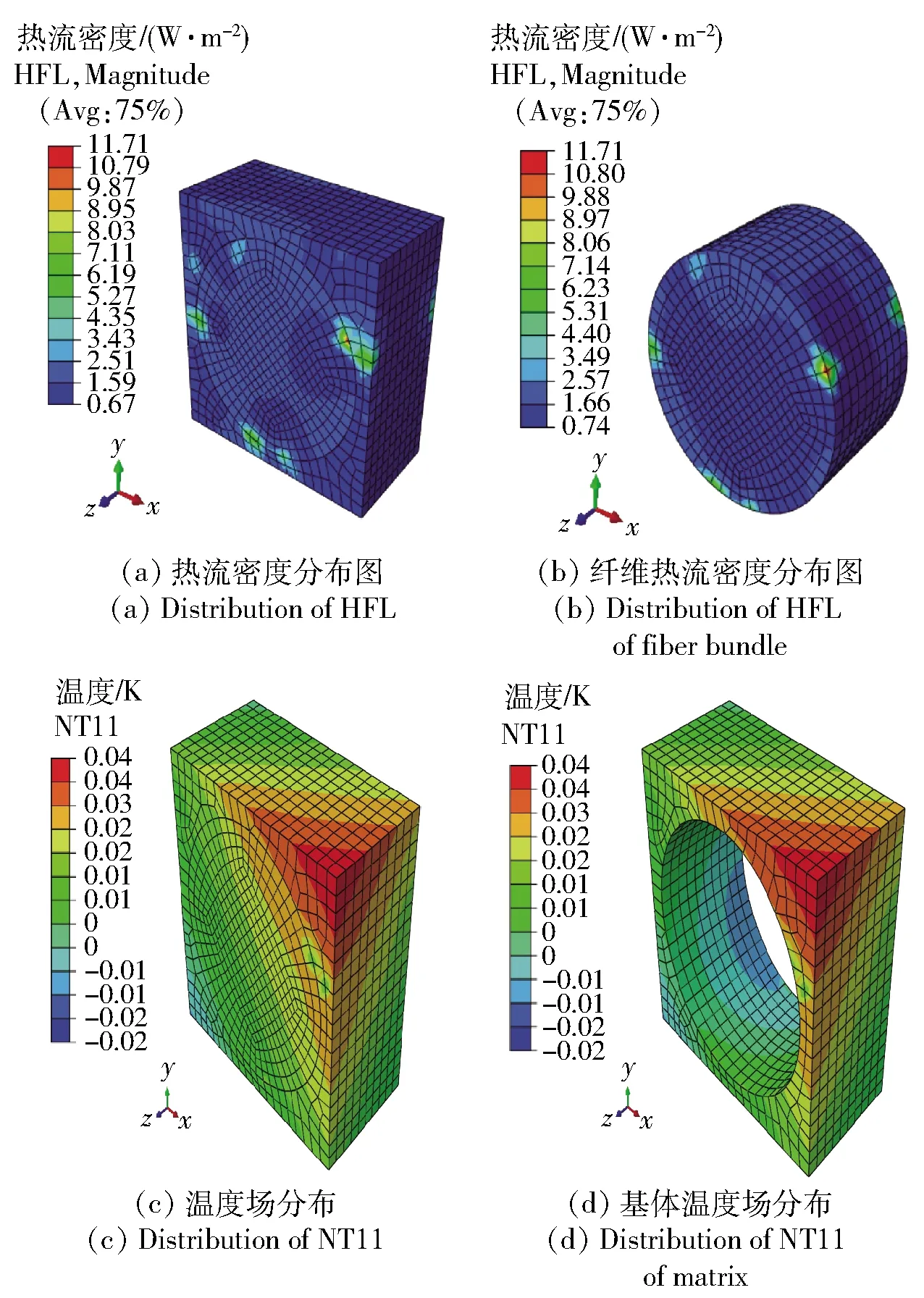
图14 立方体RVE的HFL和NT11分布云图Fig.14 Distribution of HFL and NT11 of RVE

4 结论

本文完成了轴编C/C复合材料和组分材料的微细观形貌表征实验，在微细观形貌特征的基础上完成了组分材料纤维束的微细观尺度热结构特性研究。得出主要结论如下：

1) 通过实验表征得出轴编C/C复合材料具有重复性分布特征，组分材料纤维束中的纤维单丝是随机任意分布的，截面可以等效为圆形，其余部分是基体。

2) 推导出立方体单胞和正六棱柱单胞的温度周期性边界条件计算公式，实现了纤维束不同RVE模型温度和位移周期性边界条件的施加；同时在各向同性材料上验证了本文提出的预测复合材料等效热结构参数方法的正确性；本文提出的预测复合材料等效热结构参数方法也同样适用于其他复合材料热结构性能的分析。

3) 建立的纤维束3种类型的RVE模型中，通过与实验数据对比，得出正六棱柱RVE模型在横向各向同性预测值误差最小。在受热载荷过程中，炭纤维是主要的受载荷部分。实现了RVE模型的温度周期性分布，不同材料的NT11分布相同，验证了该方法的正确性。本文提出了一种轴编C/C复合材料微细观等效热结构性能的研究方法。