基于交战进程的潜艇声感知行为机理方程

张东俊， 黎潇， 米杨

(92337部队， 辽宁 大连 116023)

0 引言

潜艇作战试验建模仿真是在贴近实战化要求和复杂环境条件下，考核潜艇遂行使命任务的能力和效能。潜艇作战的特点是隐蔽接敌并发起攻击，因此探测能力是潜艇发挥作战优势的重要度量。受水下环境因素制约，声纳探测是潜艇搜索对手的主要手段，针对声纳性能提升和改进的研究从未停止。然而，在作战使用过程中，作战人员对声纳的不同应用方式会造成声纳探测能力和效能的差异，这种差异可以影响甚至改变作战进程。因此，传统从静态性能参数角度建立的探测能力模型不能满足动态仿真推演评估系统的需求，应该研究实战应用环境中的潜艇声纳动态探测能力。

目前国内外针对潜艇探测能力的研究大致可分为两个侧重点：一是基于声纳自身装备性能的研究，目前在这方面的研究成果多为软件改进，如声纳目标跟踪算法研究[1-2]、声纳图像识别技术[3-4]等，这类研究缺乏实战条件下潜艇和声纳结合运用的考虑，仅适用于装备预先研究与更新，对现有声纳装备的运用指导意义弱；二是基于作战运用整体的研究，即在对潜艇整体作战能力的研究中涉及探测能力分析，这类研究多结合鱼雷武器使用[5-6]与防御[7]进行，从武器系统运用角度弥补探测信息短板，而非对声纳探测能力进行提升。

综上所述，现有研究甚少将作战行为和探测能力动态结合，从作战运用角度进行感知探测能力的寻优改进。因此本文提出用声感知交战行为机理方程的形式表达潜艇运动与声纳性能的关系，以得到更贴近实战运用的声纳感知能力。

交战行为机理方程即运动方程与装备机理方程的复合函数，用于揭示交战过程中基于敌我行为博弈特性的装备作战能力与效能，按照作战进程可分为感知、传递、转化3类。其中，感知交战行为机理方程指用于反映基于进程感知能力变化规律的函数集，包含声感知、压感知、磁感知、雷达感知等众多分支。本文所研究的声感知交战行为机理方程即为潜艇运动方程与声纳探测机理函数的复合函数，用于描述潜艇不同运动状态下的声纳感知能力随动特性，记作fd.

图1给出了交战行为机理方程构建的基本流程，机理方程及关键因素在第1节给出，行为与机理关联、最终机理方程表达式及其偏导应用在第2节给出。

1 潜艇运动与声感知机理函数

潜艇声感知是在运动过程中利用声纳进行的探测活动，受海洋环境、潜艇姿态、潜艇空间位置、作战行为等因素影响，本文从潜艇6自由度运动机理、声纳探测范围和声传播影响因素三方面进行分析，对原有机理模型进行推导，并结合试验数据得到统计元模型和经验模型确定机理函数的相关参数。

1.1 运动方程

运动方程指潜艇水下6自由度运动涉及的参数变量关系，用于描述潜艇行为，表征潜艇的空间坐标、姿态、分向速度和时间的关系，记作fm.

潜艇在水下的运动是一种6自由度运动，其沿各轴的运动分别称为横摇、纵摇、艏摇、纵荡、横荡和升沉，反映潜艇运动状态的水动力方程在文献[8]中给出。

影响潜艇感知探测的运动状态有潜艇的空间位置和姿态。潜艇艏摇角、艏摇角速度和横荡速度可以决定水平面运动；纵摇角、纵摇角速度和垂荡速度可以决定垂直面运动；横摇角、横摇角速度只改变潜艇姿态，对潜艇运动状态和位置变化影响可忽略不计，因此可通过6自由度方程拆分得潜艇水平面控制对象状态方程和垂直面控制对象状态方程：

水平面控制对象状态方程

(1)

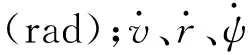
垂直面控制对象状态方程

(2)

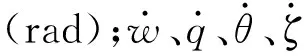
根据海上实际试验数据，对潜艇水动力方程及水平面运动对垂直面的运动耦合系数、垂直面运动对水平面运动的耦合系数进行修正，优化得出潜艇机动方程：

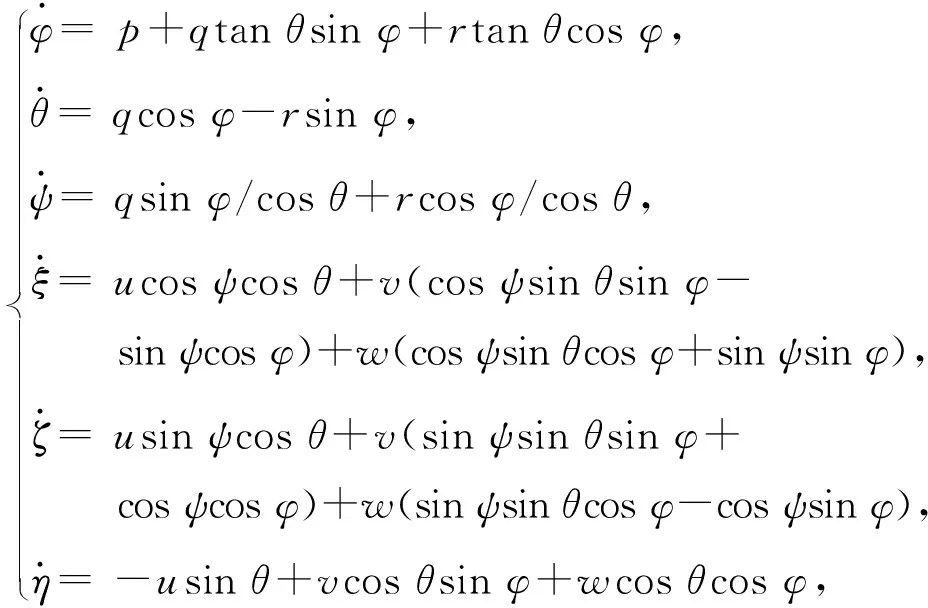
(3)

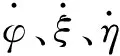
潜艇随时间变化的运动方程可以简单表述为如下形式：

(4)

式中：(x,y,z)为潜艇空间坐标；(x0,y0,z0)为初始时刻空间坐标；(φ0,θ0,ψ0)为初始姿态；t为时间。即运动方程是空间坐标(x,y,z)、姿态(φ0,θ0,ψ0)、速度(u,v,w)和时间t的函数，其中潜艇的水平面位置是随艏摇角、潜艇航速和时间变化的函数，深度由纵摇角、垂荡速度和时间决定，f1～f6由(1)式～(3)式确定。

1.2 声纳探测函数

声纳探测区域受探测距离和盲区的影响，探测距离由声传播函数确定，探测盲区和声纳的探测角度、换能器倾角、声线弯曲度等因素有关[9]，其中由于探测角度造成的物理盲区是影响探测区域的最关键因素，因此定义声纳探测函数f(R,β,γ)，表示受物理盲区影响后声纳的探测区域，其中：R为探测距离；β为水平面角度，以艇艏方向为0°逆时针旋转；γ为垂直面角度，以垂直向上为0°.

某型潜艇装有舷侧声纳和艇艏声纳，根据实测数据和声纳机理原模型，可得到其探测角度及距离，拟合成相应参数方程。艇艏声纳为类似球面阵，探测区域用参数方程可表示为

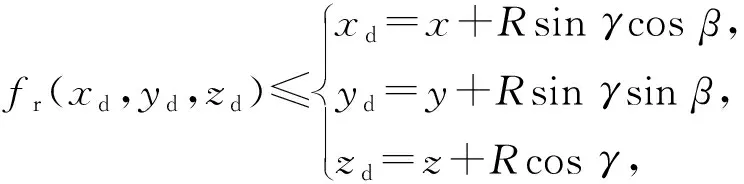
(5)

式中：(xd,yd,zd)表示探测区域坐标；[βmin,b,βmax,b]为艇艏声纳水平面角度取值范围；[γmin,γmax]为垂直面角度取值范围。

舷侧声纳分别向艇两侧辐射，形成近似双纽线状的探测范围，探测区域的参数方程为

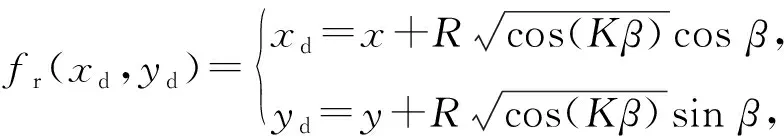
(6)

式中：K为系数；(βmin,f,βmax,f)为舷侧声纳水平面角度取值范围。在潜艇进行搜潜探测时，可单独使用其中一种声纳，也可综合使用。

1.3 声传播函数

潜艇声感知主要由被动声纳进行，定义声传播函数为fp，可通过被动声纳传播方程[9]得到：

fp=SL-TL-NL+DI-DT，

(7)

式中：fp≥0 dB表示潜艇探测到目标，fp<0 dB表示未探测到目标；DT为声纳的检测阈，即声纳测量的信噪比，与接收机带宽W、时间积分长度T有关；SL为目标的辐射噪声声源级，与信号功率谱密度有关；NL为声纳自噪声级；DI为声纳设备接收机的接收指向性指数，与阵列形状有关；TL为声波在海水介质中的传播损失。

在实际潜艇探测过程中，声纳检测阈DT不受潜艇运动影响，可看作定值，不作为函数变量，因此声传播函数的影响变量为fp(SL,NL,DI,TL)。

2 基于有限次函数复合的声感知行为方程构建

在实际作战中，潜艇运动与声纳探索并非独立的变量，声纳探测距离与潜艇所处的空间位置、航行姿态以及自噪声变化等因素密切相关，本节将潜艇运动方程中的相关变量与声纳探测机理函数通过有限次运算进行函数复合，得到随时间和作战实际情况变化的声纳探测函数。

有限次函数复合即通过一定次数的复合运算与函数叠置得到的复合函数，生成的函数能够综合表达各变量间的作用关系。本文先将实际产生关联的行为变量和声传播变量分别复合，再通过(7)式所示的规律进行复合，以此表征不同潜艇行为、不同作战态势下的声纳感知探测能力，并分析一段作战进程内的综合探测能力和变化趋势。

2.1 目标航速与辐射噪声

辐射噪声SL与潜艇的隐蔽性密切相关，敌我博弈过程中辐射噪声越大越容易被对方感知。潜艇辐射噪声主要和航速u有关，设uT为潜艇临界速度，当潜艇达到临界速度时，由于空化现象会使辐射噪声突然增大，因此航速与辐射噪声的关系可通过大量试验数据[10]拟合为

(8)

式中：s=1,2,3,4代表潜艇类型，分别为极安静潜艇、安静潜艇、噪声潜艇和高噪声潜艇；l为潜艇达到临界航速后辐射噪声随航速变化的斜率，一般取值为1.5～2.0.

2.2 作战行为与潜艇自噪声

声纳自噪声级NL是影响声传播的重要因素之一，包括声纳自噪声和海洋环境噪声，在工程上，认为一定带宽内的噪声为白噪声，因而如果声纳接收机的带宽为W(Hz)，则噪声级可表示为

NL=NLo+NLs+10lgW,

(9)

式中：NLo、NLs分别为海洋噪声和自噪声在声纳工作中心频率处的谱级[9]。

当潜艇所在海域范围和执行任务时间确定时，认为在一定时间内海洋环境噪声的变化量可以忽略不计，因此重点讨论由操舵产生的机械噪声、不同航速的桨噪声、流噪声对潜艇自噪声的影响[11-12]，即

NLs=f(u,ε(δr,δs,δb),t),

(10)

式中：ε表示在某一时刻方向舵、艏舵、升降舵变化的函数。

在航速较低时，潜艇自噪声主要来自机械噪声，舵角变化会使自噪声产生瞬时的强冲击，研究表明：舵角的大小、变化频率、转舵次数均会对机械噪声产生影响[13]；当航速大于10～12 kn时，自噪声主要来自螺旋桨噪声和流噪声，随航速增大而增大[14]。因此(10)式可简单拟合成如下形式：

(11)

式中：ns为NLs的指数形式；c、n为常数；εm为打舵次数；εw为舵角大小。当航速大于10～12 kn时，自噪声主要受航速影响，若此时潜艇为水面航行状态，其噪声功率与航速的5～7次方呈正比；当航速较低时，自噪声与舵角激励呈指数关系。

2.3 潜艇姿态与探测指向性

潜艇探测指向性fDI是指随潜艇动作而变化的可探测范围，在指向性或指向性轨迹范围内则可能被探测到。当声纳装置固定在潜艇上时，其探测能力随着潜艇运动而改变，因此其探测范围是声纳自身探测角度与潜艇横摇、纵摇、艏摇角的复合，将运动方程与声纳探测函数相结合，即将(4)式代入(5)式和(6)式，可记作：

(12)

此外，声波在海水中传播受海洋环境影响，需综合考虑潜艇所在位置的海洋声传播信道，一般情况下使用的射线模型是基于入射角变化的模型，其传播距离受声波角度影响，即潜艇探测过程中声纳平台的指向性、噪声源的指向性变化均会对传播距离造成影响，因此在研究探测指向性时，考虑环境模型因素。射线模型形式如下：

p=f(x,y,z)eig(x,y,z),

(13)

式中：f()为幅度函数；g()为相位函数。则潜艇的探测指向性函数fDI在考虑行为的影响下可表示为

fDI=fDI(p(x,y,z),fr(ψ,θ,β,γ,R),t).

(14)

2.4 潜艇深度与传播损失

传播损失TL由几何扩展损失和介质吸收损失二者构成，潜艇位于水下不同深度，其传播损失随之改变。在浅海，根据深度的变化要考虑均匀层和负梯度声场的衰减；在深海，要考虑混合层声道、SOFAR声道、会聚带及海底反射导致的衰减，详细的函数关系描述可见文献[15]。在进行有限次函数复合时，本文取潜艇一般潜航深度下的经验公式，此时的传播损失为

TL=20lgd+αd,

(15)

式中：d为距离；参数α=0.036f3/2，f为声纳工作频率[9]。

2.5 声感知交战行为机理方程的综合表达

对(7)式进行指数变换，非变化的常量用c表示，得到声传播函数的指数形式为

(16)

2.1节～2.4节分别将fp(SL,NL,DI,TL)中的各个变量与潜艇运动行为进行关联，得到对应复合函数表达式，将 (8) 式、(11) 式、(14) 式和(15)式代入 (16) 式，可得到考虑潜艇运动后的声传播函数表达式为

(17)

式中：uw表示我艇航速；ud表示对手航速；fh(εm,εw,t)为舵角函数。从(17)式可以看出，在水下声探测能力受敌我速度、敌我距离的影响最大，随敌我距离的增大和敌方速度的降低而呈指数倍的衰减，同时与自噪声呈反比，与指向性函数呈正比：敌方运动速度越大、我方运动速度越小、敌我距离越小、自噪声越小、指向性越大，越容易感知。

通过(17)式可以得到当声传播函数为0时的敌我距离，即可探测到的临界距离，将该距离代入声纳探测函数，就可以得到一定运动行为下的潜艇探测范围，即所求的声感知交战行为机理方程。该方程包含运动行为和声纳感知各要素，反映随行为变化的声纳感知能力，其综合表达式为

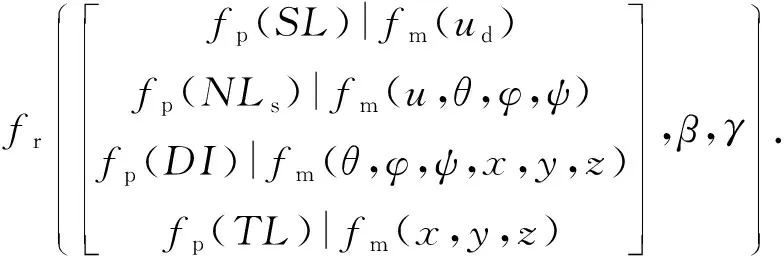
(18)

(18)式表示在某一时刻下，不同潜艇运动状态的声纳传播距离和探测范围随之发生变化的函数关系，即潜艇交战过程中的实时探测能力。

2.6 声感知能力及变化趋势分析

对声感知行为机理方程在一段时间内进行积分，可得到该时段内声纳综合感知能力，再分别对各变量求偏导，即可得到声感知能力在不同变量作用下的变化趋势：

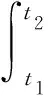
(19)

(19)式表示[t1,t2]时间段内总的声纳感知能力，以时间为横轴、声纳探测能力为纵轴绘制曲线，可以得到随时间进程改变的声纳探测能力变化图，由于潜艇行为也随时间发生改变，因此该曲线可体现声纳的时变及随动特性。

根据(18)式中所涉及的变量，可以分别从5个方面的变量入手对(19)式求偏导，得到不同条件下的声纳感知能力变化趋势。为简化表达式形式，更直观地反映所关注变量的影响，下文中将无关变量用系数A、B、C表示。

2.6.1 对时间偏导

2.6.2 对潜艇姿态变量偏导

潜艇姿态指潜艇横倾、纵倾等变化，主要改变潜艇的探测指向性，通过1.1节相关公式可知，潜艇的横摇角、纵摇角、艏摇角和声纳探测能力之间为线性关系，对其求偏导可直接得到该姿态下的变化率，如：

(20)

2.6.3 对潜艇行为变量偏导

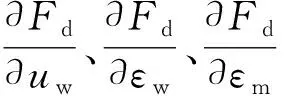
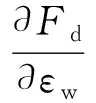
(21)

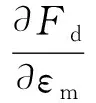
(22)

由于A为非负，则其变化率为负值，即探测能力会随着舵角的频繁变化以及舵角的增大而呈下降趋势。

(23)

对我潜艇航速求导可得到一个负变化率的曲线，但物理意义不大。

2.6.4 对敌我距离偏导

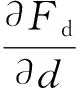
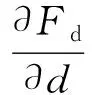
(24)

2.6.5 对敌航速偏导

一般情况下，敌航速对我方是未知目标，很难得到其数值，因此通过综合感知能力对ud偏导，可用于研究敌方行为，但由于二者之间非线性，需要对航速进行多阶偏导，1阶偏导结果为

(25)

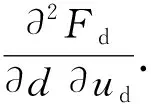
3 仿真及实例验证

3.1 仿真验证

在声感知行为机理方程中，涉及敌方行为和我方行为两方面要素，由于敌行为不可知性，本节采取仿真的方法进行敌方变量验证，通过试验数据进行我方变量验证。

仿真条件如下：我航速小于12 kn，初始敌我距离d=40 Cab，敌潜艇以航速10 kn不断靠近，发现我潜艇目标后打方向舵加速驶离，仿真结果如图2～图4所示。

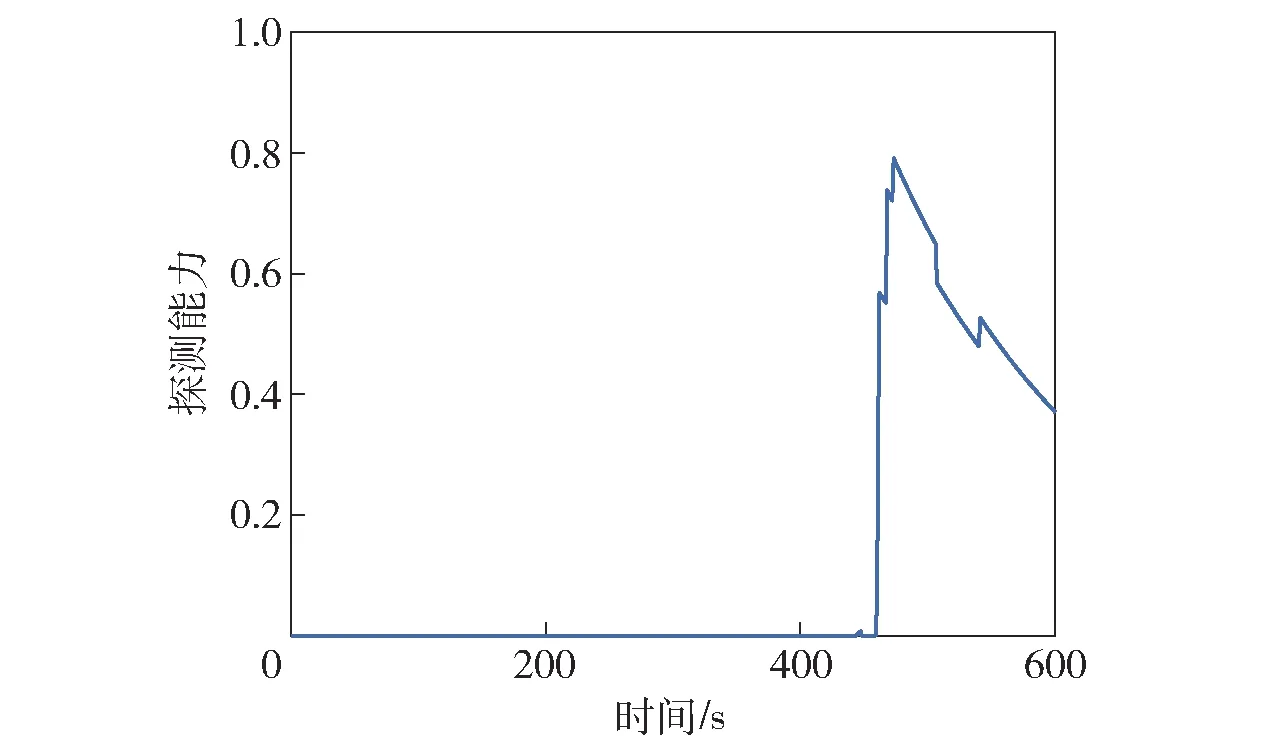
图2 探测能力随时间变化曲线Fig.2 Detection ability versus time

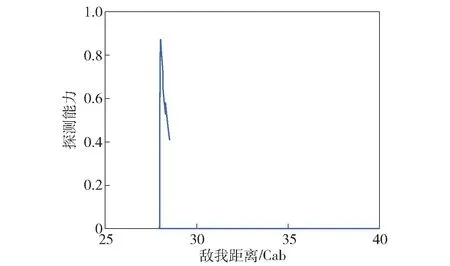
图3 探测能力与敌我距离关系曲线Fig.3 Relationship between detection ability and distance

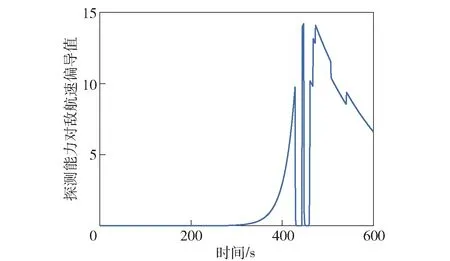
图4 探测能力与敌航速变化曲线Fig.4 Relationship between detection ability and enemy motion speed

图2给出探测能力随时间变化的曲线，曲线反映了450 s之前，敌潜艇不在我探测范围内，460 s左右进入探测临界范围内，探测到目标，但敌采取规避行为后探测能力逐渐减弱。

图3反映了探测能力与敌我距离的关系，从中可以看出我潜艇在相距28.5 Cab左右的时候可发现目标，随着距离的减小探测能力不断增大，大于29.0 Cab时无法探测到目标。

图4是对敌航速求高阶偏导后的曲线，曲线反映了在426 s、451 s、476 s附近敌航速发生明显变化，对应敌发现目标后回转并加速驶离过程。

3.2 实例验证

以潜艇声纳性能试验和潜艇机动性能试验数据为基础，建立潜艇声感知行为机理方程，分别选取变深、变向和变速时的数据，分析声纳探测范围的影响因素。

3.2.1 潜浮行为对声纳探测能力影响

潜艇初始航速6 kn，深度8 m，初始航向0°，探测目标为18 kn高噪声水面目标。潜艇艏倾3°从水下8 m下潜至水下30 m.

按照声感知机理方程构建方法，建立潜艇下潜过程的声感知能力随深度变化的函数关系：

f(z)=107.6sin(0.076 42z+0.684 3)+
89.74sin(0.086 83z+3.634)+
0.653 4sin(0.638 5z-5.328)，

(26)

式中：z为深度。探测能力数据如图5所示。

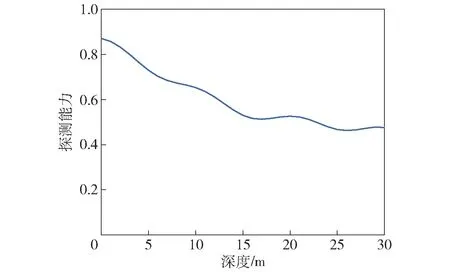
图5 潜艇下潜过程声感知能力变化图Fig.5 Changing curve of acoustic detection ability during diving

由图5可以看出：潜艇下潜过程中声纳探测能力与声速梯度密切相关；深度为0～30 m内声速梯度为弱负梯度，声纳探测能力随深度变化总体呈下降趋势。同时，从图5中数据看，曲线并不是平滑的下降，这是由于潜艇下潜过程中姿态发生了一系列变化，导致了声纳探测能力的改变。从水下8 m时纵倾开始变化，由无纵倾变为艏倾3°，整个下潜过程保持艏倾不变的状态范围，潜艇在接近25 m时，由艏倾3°变为无纵倾，声纳探测能力在总体呈现下降的基础上有轻微波动的现象。

3.2.2 变向对声纳探测能力影响

潜艇搜索目标潜艇时，通常采用不定时变向的行为，以提高潜艇发现概率。以潜反潜过程中的之字形搜索为例说明变向对声纳探测能力的影响。潜艇航速6 kn、航向300°，方向舵舵角变化5°，转向60°；目标潜艇航速8 kn，航向0°，曲折机动。

建立潜艇转向过程的声感知能力随方位变化的函数关系：

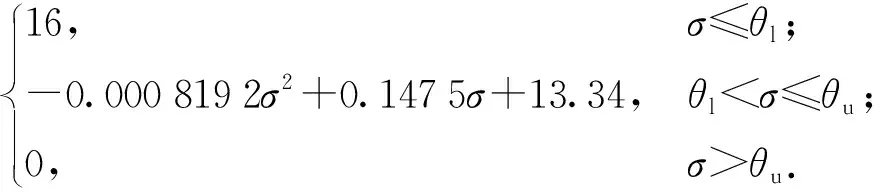
(27)

式中：σ为目标舷角；θu、θl分别为盲区界限的上限、下限。潜艇转向过程探测能力数据如图6所示。

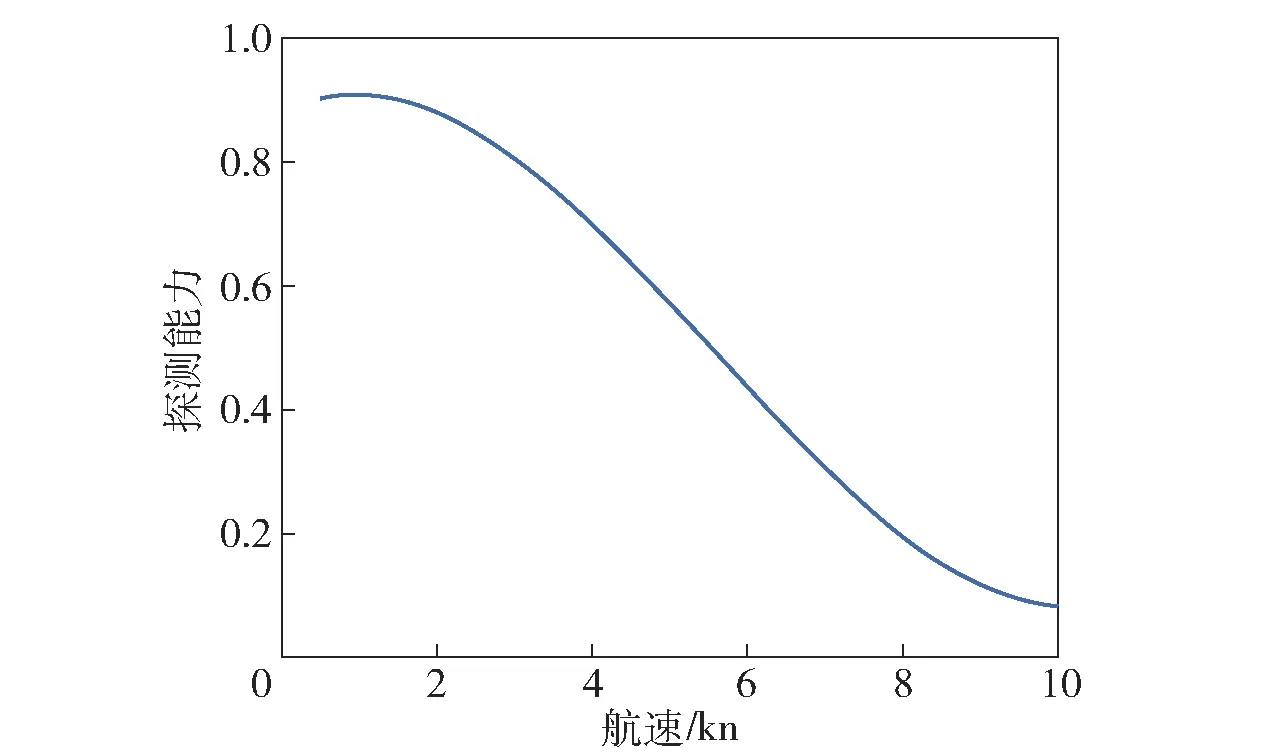
图6 潜艇转向过程探测能力变化图Fig.6 Change of detection ability during steering

由图6可以看出，潜艇水平变向机动时方向舵带来的自噪声变化会微弱降低声纳探测距离，对声纳探测能力影响较小。当航速较高时，变向几乎不改变声纳探测距离。潜艇转向带来声纳探测圈方向的改变，在实际作战中，潜艇转向使敌我相对角度变化，将导致声纳探测能力发生重要改变。当潜艇直线航行时，敌潜艇位于我艇声纳的探测盲区，当潜艇转向时，敌潜艇进入我声纳探测范围，转向行为对于提高探测概率有重要意义。

3.2.3 变速对声纳探测能力影响

潜艇工况转换，深度25 m，航速由u1加速至u2. 建立潜艇转向过程的声感知能力随速度变化的函数关系如下：

f(u)=0.054 24u3-0.905 1u2+1.636u+21.94.

(28)

声纳探测能力数据变化如图7所示。

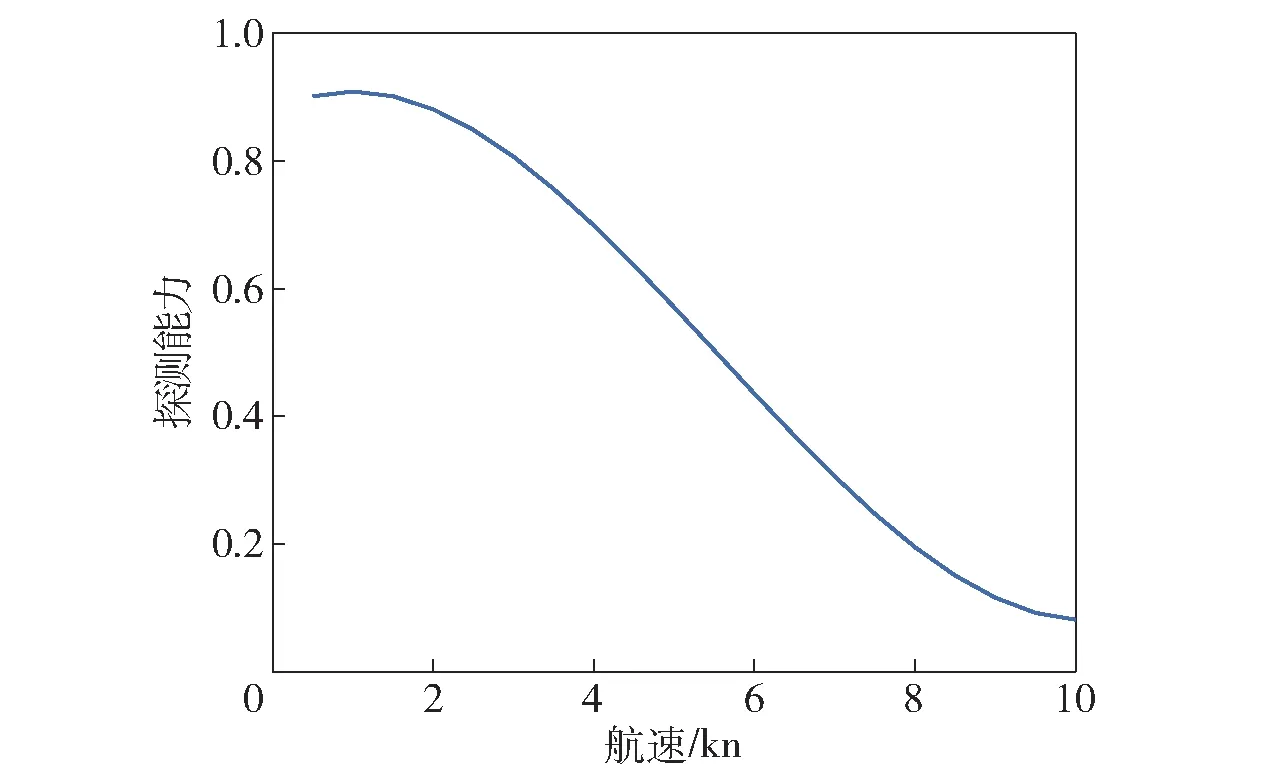
图7 潜艇加速过程探测能力变化图Fig.7 Change of detection ability during accelerating

由图7可以看出，随着潜艇航速的提升，噪声不断增大，潜艇探测距离急剧下降，印证了声纳探测能力与操艇行为呈负指数关系。从图7中数据可推算出声纳探测能力与航速的n次幂呈反比，但受试验数据精度所限，具体参数还不够精确，要想得到精确的函数关系，需进一步进行试验获取数据。

上述分析与交战行为机理方程所反映的声纳探测能力变化规律吻合：航速的变化对噪声和声纳探测距离造成较大直接影响，操舵等机械噪声在高航速下几乎不造成影响、在低航速下略有影响，在同一声速梯度下的深度变化对探测距离影响不大。此外，变深过程中艏倾的改变会造成指向性变化，探测能力相应改变，在相关战法中已得到验证，其他影响因素有待进一步试验验证。

4 结论

针对静态声探测能力指标不能满足动态仿真推演评估需求的问题，本文提出了声感知交战行为机理方程构建方法，将操艇行为、潜艇运动状态和声纳探测性能在时统下进行关联，求得不同战场态势下行为对应的实时声感知能力。案例研究验证了交战行为机理方程计算得到的声纳探测能力变化值与航行试验数据结果的一致性。该方程能够定量刻画声纳探测能力随潜艇姿态、空间位置、航速等运动变量变化的行为随动规律，并且通过对方程的影响因素进行微积分运算支持声感知能力变化趋势分析，为构建潜艇作战试验动态仿真推演评估系统提供了基础模型支持。

下一步工作包括以下三个方面：一是在更广的作战试验内采集更多的数据样本对机理方程进行拟合和验证，提高方程的精确性和扩大适用范围，对复合方程进行具体化；二是根据探测、隐蔽、打击、防护等作战行为之间的关联关系，在总体作战能力约束条件下研究探测能力的决策优化；三是拓展机理方程的应用领域，支持潜艇搜索策略、作战方案生成及战法训法创新等研究。