基于联合估计迭代算法的三轴磁力仪标定补偿方法

孙欢， 杨宾峰， 管桦， 王润

(空军工程大学 信息与导航学院， 陕西 西安 710077)

0 引言

近年来，地磁导航发展迅猛，其隐蔽性强、自主性高、抗干扰能力强的特点，使得地磁导航在水下、电磁环境恶劣的空域，有着明显优势和广阔的发展前景[1-3]。

地磁传感器的观测精度将直接影响导航精度，但在实际测量过程中，地磁信号和各类误差信号相互耦合，组成了地磁传感器输出，严重影响了地磁场测量精度，抑制了磁力仪潜在性能的发挥。因此对于地磁传感器进行标定和补偿，对提高地磁匹配导航的精度有着重要意义[4-7]。

针对地磁传感器的误差补偿问题，国内外学者进行了诸多研究。Renaudin等[8]在磁场域对各向异性磁阻传感器的校正问题进行了研究，其详细分析了传感器自身仪表误差、软磁以及硬磁误差的来源和产生机理，建模时将这些误差都予以充分考虑；文献[9-10]对地磁传感器测量误差和软、硬磁误差进行一体化建模，前者采用椭球拟合校准法进行补偿，后者考虑到观测向量和数据矩阵均存在误差，因此用总体最小二乘进行了补偿。对于以上矢量建模方式，仍然不能精确地表示载体内磁场的真实状况。涡流磁场及相关的低频磁场是由于载体的姿态变换所产生的，涡流磁场不依赖于载体的铁磁性，而只依赖于其导电性能[11]；文献[12] 采用多物理仿真软件Comsol Multiphysics建立了载体涡流干扰场的仿真模型，并进行定性分析；文献[13]提出了一体化建模的思想，并对旋转速度等特性做了研究。

对于磁场补偿算法，目前主流的算法有航磁补偿法、两步估计法、椭圆拟合法及无迹卡尔曼滤波(UKF)算法。航磁补偿法[11,14]是基于Tolles-Lawson方程，将地磁场测量值的三分量均投影在地磁场方向，但忽略了地磁场真实值和测量值方向之间的误差，因此只适用于干扰场较小的情况；在两步估计算法[5,10]中，由于中间变量的存在，各个参量的相关性可能出现系数矩阵奇异，从而无法正确解算；椭圆拟合法[15-17]要求测量值要拟合出一个椭圆，从而建模方式比较简单，难以适应复杂的测量环境；UKF算法[18-19]能够实现高精度的实时补偿，但对初值敏感度高，选取不当可能造成滤波发散，得不到正确结果。

通过分析，以往研究对载体内涡流磁场及双噪声研究不足，缺少一体化模型和高效的补偿算法。本文针对此问题进行一体化建模，提出了基于联合估计的迭代算法，并与扩展卡尔曼滤波(EKF)算法和非线性最小二乘算法进行性能比较。该方法具有良好的仿真和实验性能，可用于提高三轴磁力仪的测量精度。

1 误差补偿模型

根据以往研究[20]，地磁传感器误差模型可以表示为

B=CH+b+ε，

(1)

式中：B为地磁传感器测量值；H为地磁场真实值；C=CMCNOCSFCSI，CM为地磁传感器安装于载体过程中传感器和载体3个轴完全不重合所产生的误差矩阵，CNO为传感器内部三轴不完全正交所引起的误差矩阵，CSF为制作工艺所产生的刻度因子误差，CSI为载体内软磁误差系数矩阵；b=CMCNOCSFCSIBh+w+bs，Bh为载体内硬磁材料所产生的干扰，w为传感器内部零刻度漂移误差，bs为传感器的剩磁误差；ε为测量过程中的观测噪声，以往研究表明，ε呈高斯分布。

对于高速、频繁作姿态变换的载体，其内部会产生涡流，进而产生涡流磁场，影响传感器的精确测量。研究表明，涡流磁场强度与在体内部涡流呈线性比例关系，而涡流强度又与单位时间磁通量的变化呈线型比例关系，将比例系数矩阵整合，考虑涡流磁场在内，可得模型[21]：

(2)

式中：k代表第k次求解，k=1,2,…，n，n为数据总量；P为整合后的涡流磁场与单位时间内磁通量变化的比例系数矩阵。

变换得地磁场真实值的表达式为

(3)

式中：Q=C-1，在(3)式中，参数空间维数Θ为

dimΘ=elements(Q)+elements(b)+
elements(P)=21.

(4)

由上文分析可知，Q在本文所设环境下为非奇异矩阵，即仪表误差和载体干扰磁场误差必然存在(即使很小)，因此对参数矩阵Q进行QR分解如下：

Q=QARA.

(5)

经过QR[22]分解，将Q参数矩阵分解为正交矩阵QA和上三角矩阵RA，将(5)式代入(3)式并取模，得

(6)

由于QA、RA是唯一的，因此在保证参数矩阵的唯一性基础上，将参数空间由21维降到了18维，得模型如下：

各参数矩阵表达式为

当各个系统参量明确时，即能对地磁场测量值实现补偿，因此设参数向量Xk为待求量：

Xk=[vecs(RA)T,bT,vecs(P)T]T=
[q11,q12,q13,q22,q23,q33,b1,b2,b3,p11,
p12,p13,p21,p22,p23,p31,p32,p33]T.

(7)

2 补偿算法

2.1 EKF算法

(8)

式中：RAk为RA在第k次的值；νk为观测噪声。

则该问题的状态方程和观测方程可以表示为

Xk=fk(Xk-1)+ηk,

(9)

(10)

fk(Xk)=Xk,

(11)

(12)

(13)

式中：设系统噪声ηk为均值为0，协方差矩阵为Q的高斯噪声。

由(13)式，观测噪声的均值μk和方差R可表示为

μk=E[vk]=-tr(Σ),

(14)

(15)

Σ={εεT}.

(16)

k|k-1=fk(k-1),


k=k|k-1+Gk(Zk-hk(k|k-1)),
Pk=(I-GkJk)Pk|k-1,

(17)

在EKF初值设置中，X0取经验值，P0可以取较大，由于数据量充足，经过k次求解最后得到Xk即为所需参量值。

2.2 非线性最小二乘算法

在非线性最小二乘算法处理时，由于可以经过多次测量取平均值，因此可以将系统噪声ηk与观测噪声εk忽略掉，根据(6)式，地磁场补偿模型变换为

(18)

则地磁场真实值的标量值即为

(19)

测量值与真实值的差值可以表示为

(20)

经过k次测量，对差值求和可得总差值表达式为

(21)

根据非线性最小二乘算法原理，当E取得最小值时，X取得最优解，即X=argmin(E)，进而得到补偿模型中的各个系统参量。

2.3 联合估计迭代算法

根据上文，地磁场补偿模型为

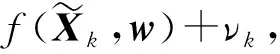
(22)

(23)

这同样是关于X和w的二次优化问题，因此存在闭合解，如(25)式所示。

(24)

(25)

(26)

3 数值仿真

利用仿真数据对上述算法进行验证，根据(2)式所述地磁场观测值模型，设地磁场真实值为50 000 nT， 为了模拟载体姿态变换，设置球坐标系下转动变量θ和γ，当地磁场真实值3轴分量如下产生：

地磁场3个轴的分量值将会随θ和γ的变化而变化，从而模拟载体姿态变化。

设观测过程中系统噪声、观测噪声服从均值为0 nT，标准差分别为10 nT和50 nT的高斯分布，且相互统计独立，为了更好地说明补偿效果，本文采用误差均值E(n)和标准差δ进行分析：

(27)

(28)

式中：Bi为每次的测量总值；Bm为测量值均值；B0为该地磁场的真实值。

在仿真中，设置不同转动频率，从而改变载体内涡流磁场的强弱，得地磁场测量值如图1所示。

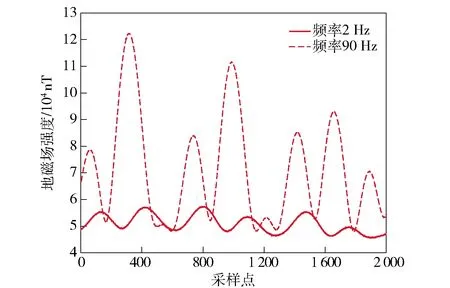
图1 不同转动频率下地磁场测量值Fig.1 Geomagnetic field measurements at different rotational frequencies

由图1可知，当载体瞬时转动频率较大时，其内部的涡流磁场将严重影响地磁传感器的精确测量。提取仿真数据中50 Hz转动下的地磁场观测数据，用本文所提联合估计迭代算法分别对有无涡流磁场项的模型进行补偿，验证含涡流磁场一体化模型的有效性，结果如图2所示。

图2 不同模型补偿结果Fig.2 Compensated results of different algorithms

图2结果表明，含涡流磁场项的一体化模型有效滤除了由涡流磁场引起的波动干扰，使补偿结果更加精确稳定。对以上仿真数据，分别采用EKF算法、非线性最小二乘算法和联合估计迭代算法进行处理，得到各参量解算值，而后用这些值进行误差补偿，比较各个算法实用性。经过解算，各系统参量的预设值和解算值如表1所示。

由表1可知，3种算法均能对系统参量实现补偿，其中，非线性最小二乘算法由于未考虑噪声影响，因此补偿效果次于其他两种算法。3种算法补偿情况如图3～图7、表2所示。

如图3所示，EKF算法补偿时，任取参数中的两个值分析其收敛情况。由图3可看出，在经过大约400组数据的运算，各参数收敛并趋于稳定，因此在补偿初始阶段，整体补偿效果不理想。EKF算法整体补偿效果如图4所示。非线性最小二乘算法由于未进行降噪处理，补偿结果有较大误差(见图5)。联合估计迭代算法无论是地磁场分量还是总量均能够实现较好的补偿(见图6、图7)，各算法补偿结果数据如表2所示。

仿真结果表明：非线性最小二乘算法补偿结果误差较大，另外两种算法均可实现精度较高的补偿，但EKF算法补偿精度对数据量的依赖较大(由图1可知，在本文仿真中，当数据量少于400组时，参数不能收敛，无法做到高精度的补偿)；联合估计迭代算法相比于其他两种算法，补偿精度最高，抑制比可以达到94.08%.

表1 预设参数与不同算法解算值

注：XP为预设参数；XE为EKF算法解算值；XN为非线性最小二乘算法解算值;XJ为联合估计迭代算法解算值。

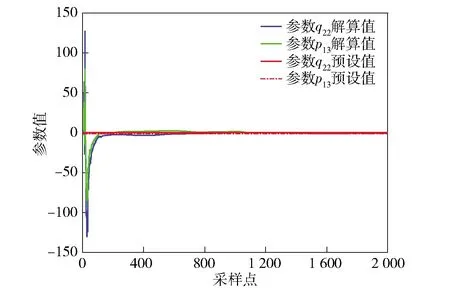
图3 EKF算法部分参数收敛情况Fig.3 Partial parameter convergence of EKF algorithm

图4 EKF算法补偿效果(仿真数据)Fig.4 Compensation effect of EKF algorithm (simulation data)

图5 非线性最小二乘算法补偿效果(仿真数据)Fig.5 Compensation effect of nonlinear least square algorithm (simulation data)

图6 联合估计迭代算法整体补偿效果(仿真数据)Fig.6 Compensation effect of joint estimation iterative algorithm (simulation data)

图7 联合估计迭代算法各分量补偿效果(仿真数据)Fig.7 Compensation effect of joint estimation iterativealgorithm (simulation data)

表2 不同算法补偿结果(仿真数据)

Tab.2 Compensated results of different algorithms(simulation data)

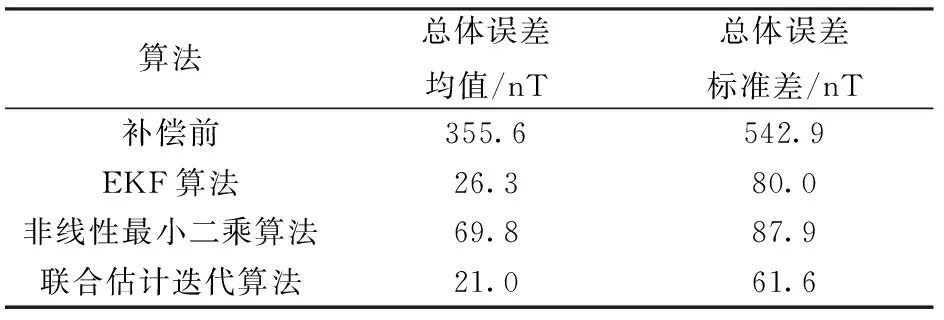
算法总体误差均值/nT总体误差标准差/nT补偿前355.6542.9EKF算法26.380.0非线性最小二乘算法69.887.9联合估计迭代算法21.061.6

4 实验设计

4.1 实验系统

在实验设计中，采用英国Bartington公司的Mag-690-FL100(测量精度0.1 nT)三轴磁力仪进行补偿，将其置于1∶48飞行器缩比模型上方模拟真实情况下处于飞行载体内部的情况。为模拟飞行载体姿态变化，选用3FHT30C无磁转台提供姿态信息，该转台剩磁为7 nT，测量系统采用12 V直流电源进行供电以隔绝市电电压不稳产生的不良影响。数据采集软件用National Instruments，实验系统如图8、图9所示，后期用数值分析Matlab软件进行数据处理。采用DM050质子磁力仪提供地磁场真实值。

图8 地磁场测量系统Fig.8 Geomagnetic field measuring system

图9 地磁场数据采集系统Fig.9 Geomagnetic data acquisition system

4.2 实验步骤

1)实验场所选在远离强磁干扰的空旷地点，利用水平仪对无磁转台进行调整，将3轴磁力仪固定好之后，在下方放置飞行器缩比模型，用以仿真飞行载体内部产生的软硬磁误差及其他干扰。

2)连接好设备，接通直流电源，将数据采集软件采集频率设为50 Hz，进行连续数据采集，沿转轴快速旋转无磁转台进行全方位姿态信息测量。模拟飞行载体的姿态转动，快速转动时，瞬时速度较大，因此所采集数据中含有涡流磁场。采集所得数据用Matlab进行后期处理。

3)转动无磁转台，将地磁传感器3轴分别对准东、北、天，所得数据即为导航坐标系下地磁场值的各轴分量；无磁转台转动过程中，每一个姿态对应一个三维角度值，分别为内框、中框和外框的转动角度(显示于数显箱，记录于采集数据中)，即地磁传感器3轴偏离初始值的角度，分别记为α、β、γ，由此可以解算得到每一个姿态下地磁场3轴分量的真实值[22]：

式中：Bxk,Byk,Bzk为第k个姿态时地磁场各轴分量真实值；Bx0,By0,Bz0为初始状态地磁场各轴分量真实值。

5 实验结果

在实验中，首先采用质子磁力仪测得实验场所的地磁场值为46 157 nT，对于实验数据依次采用EKF算法、非线性最小二乘算法和联合估计算法进行补偿，其中，EKF算法初值设置为

经过3种算法补偿，补偿效果图如图10～图12所示。

图10 EKF算法补偿效果(实验数据)Fig.10 Compensation effect of EKF algorithm (experimental data)

图11 非线性最小二乘算法补偿效果(实验数据)Fig.11 Compensation effect of nonlinear least square algorithm (experimental data)

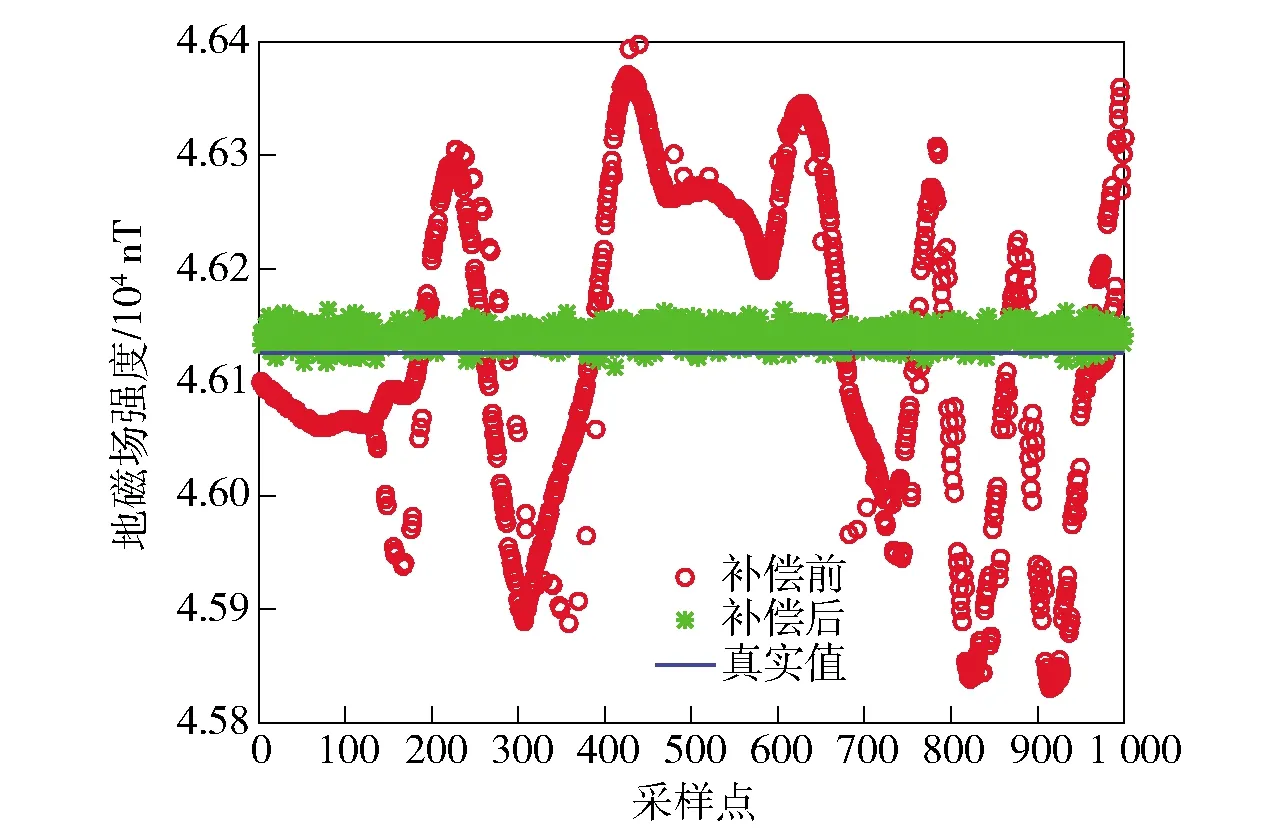
图12 联合估计迭代算法补偿效果(实验数据)Fig.12 Compensation effect with joint estimation iterative algorithm (experimental data)

由图10～图12可以看出：实验结果与仿真结果基本一致；实验采用的1 000组数据，因为初值设为0向量，EKF算法经过约300组数据后趋于收敛，在前期补偿效果次于其他两种算法；非线性最小二乘算法补偿结果依然有较大噪声干扰；联合估计迭代算法法收敛速度快，且补偿效果良好。

各算法补偿结果均值和方差如表3所示。

由表3可知，联合估计迭代算法相较于其他两种算法优势比较明显，可以将补偿误差均值由142.4 nT缩小至12.5 nT，标准差由170.0 nT缩小至37.2 nT，抑制比达到84.51%. 考虑到无磁转台剩磁误差达到7.0 nT，且实验环境周边其他干扰，因此本次实验结果对本文所提理论进行了验证，具有实际意义。

表3 不同算法补偿结果(实验数据)

6 结果分析

1)EKF算法原理简单，能够在较短的时间内实现较高精度的补偿。在模拟仿真中，EKF算法经过约500组数据达到收敛，所解算参数可用于补偿，而其他两种算法皆用2 000组数据进行参数解算，体现出EKF算法在时效性方面的优越性，但卡尔曼滤波算法对初值的依赖度很高。在本文实验中，由于对系统参量的先验知识不足，因此将初值取0向量，协方差矩阵取得比较大，由于数据量大，以此后期也能达到较好的补偿效果。对于1阶EKF算法补偿精度不够的问题，因为在本文所研究模型为弱非线性，因此其补偿精度在可接受范围之内。

2)在实验过程中，快速转动无磁转台使得飞行器缩比模型内部产生涡流磁场，对3轴磁力仪的测量产生影响，体现在测量值有较大的波动，含涡流磁场的一体化模型在建模过程中考虑到涡流磁场信息，因此相比于不含涡流磁场的模型，能够较好地滤除波动，使补偿结果更加稳定。

3)对于观测系统系统不稳定的问题，在数学上体现为各系统参量的变化，在该实验中，选取新的实验场所、调平无磁转台及进行全姿态测量过程中都会使得系统参量发生微小改变，势必将产生系统误差。对于该误差，本文将其简化为零均值高斯噪声，取得了较好的补偿效果，为了更进一步提高补偿精度，应该对该误差进行更深入的研究。

4)在采用非线性最小二乘算法处理时，对于噪声采取多组数据求均值的方法进行处理，但求均值的本质依然是含噪的。仿真和实验结果表明，该算法机理对于本问题的局限性导致补偿结果相比于其他两种算法误差偏大。

5)质子磁力仪测量误差很小，因此将所测地磁场值作为实验场所真实值。本文提出含涡流磁场和双噪声的一体化模型，含有信息种类更全，模型更完整，补偿中更有优势；在联合估计迭代算法中将观测系统噪声和测量噪声进行联合估计处理，补偿效果表明该方法比非线性最小二乘算法有着更高的补偿精度，比EKF算法补偿结果收敛更快，证明了该补偿模型和补偿方法的开发潜力。

7 结论

地磁场测量值误差补偿向来是地磁导航中一个关键问题。本文针对载体中所含涡流磁场和双噪声的问题，提出了双噪声联合估计迭代算法对Mag-690-FL100地磁传感器进行标定，并与EKF算法、非线性最小二乘算法进行比较。仿真和实验结果表明，联合估计迭代算法补偿效果更好，该方法原理简单，对数据量依赖小，实用性强，有利于提高地磁导航系统的精度。