基于纹理特征的层次化图像配准方法*

赵夫群李艳华

（1.咸阳师范学院教育科学学院 咸阳 712000）（2.黄河科技学院信息工程学院 郑州 450000）

1 引言

图像配准就是通过定义相似性度量函数和优化策略来寻找两幅图像间的空间变换的过程，从而使得两幅图像上的对应点达到空间上的一致。配准的结果应使两幅图像上所有的信息点，或者至少是所有对分析识别具有重要意义的点都达到匹配。目前，图像配准已经在多模图像融合、航空影像处理以及医学手术导航等领域［1～5］得到了广泛的应用。

常用的图像配准方法有三类，即基于灰度信息的配准方法、基于变换域的配准方法和基于特征的配准方法。基于灰度和变换域的配准方法受光照影响大，对灰度变换敏感，配准精度较低。而基于特征的图像配准方法则可以较好地避免这些缺点，而且图像中的特征数目比较少，特征间的匹配度量随着位置的变动比较大，可以利用图像之间特征的几何约束关系，对于干扰变形有很强的适应能力，因而得到了广泛的应用。

通常所说的图像特征大多是指图像中的点、线、轮廓、区域或边缘等特征。GE等［6］提出一种基于关键点特征的图像配准方法，大大提高了配准的精度；XU等［7］提出一种基于特征区域的图像配准方法，通过对特征区域的相似性匹配实现了图像的稳定、精确配准；WANG等［8］采用一种鲁棒的改进Sobel特征描述子来实现图像配准，大大提高了配准精度和速度；HOU等［9］提出一种基于Gabor尺度不变特征变换的配准方法，并将其应用到光学卫星图像配准中，提高了配准的鲁棒性和精度；屠睿博等［10］提出一种基于随机森林算法的特征点提取方法，并将其用于小鼠micro-CT影像中骨骼关节的特征点定位。

虽然以上基于特征的图像配准方法在配准精度和速度等方面有了一定程度的提高，但是对于存在明显形变的纹理图像的配准效果并不好。为了提高图像配准的精度，本文提出一种基于纹理特征的层次化图像配准方法。该方法分为粗配准和细配准两个阶段来实现，首先采用基于互信息的优化蚁群算法对图像进行粗配准；然后在ICP算法的基础上，通过对纹理特征点赋予递减权重实现基于纹理特征的图像细配准，可以使得匹配的点对在图像的纹理细节上相似，大大提高算法的配准精度。

2 基于改进蚁群算法的粗配准

2.1 蚁群算法模型

蚁群算法是受自然界中蚁群的集体行为的启发而提出的一种群体模拟进化算法，属于随机搜索算法［11～12］。蚁群算法可表述为在算法的初始时刻，将m只蚂蚁随机地放到n座城市，此时任意两座城市路径上的信息素量相等。设路径上的初始信息素τij(0)=c（c为一较小常数），每只蚂蚁根据路径上残留的信息素量和启发式信息（两城市间的距离）独立地选择下一座城市，在时刻t，蚂蚁k从城市i转移到城市j的概率pikj(t)为

式中，Jk(i)={1，2，…，n}-tabuk表示蚂蚁k下一步允许选择的城市集合。列表tabuk记录了蚂蚁k当前走过的城市，当所有n座城市都加入到tabuk中时，蚂蚁k便完成了一次周游，此时蚂蚁k所走过的路径便是旅行商（TSP）问题的一个可行解。ηij是一个启发式因子，表示蚂蚁从城市i转移到城市j的期望程度，通常ηij取城市i与城市j之间距离的倒数。α和β分别表示信息素和启发式因子的相对重要程度。

当m只蚂蚁均完成一次周游后，各路径上信息素的值为

式中，ρ(0＜ρ＜1)表示路径上信息素的蒸发系数，1-ρ表示信息素的持久性系数；表示本次迭代边ij上信息素的增量；Δτkij表示第k只蚂蚁在本次迭代中留在边ij上的信息素量，如果蚂蚁k没有经过边ij，则表示为

其中，Q为正常数，LK表示第k只蚂蚁在本次周游中所走路径的长度。

2.2 基于互信息的优化蚁群算法

互信息法是基于灰度相似性图像配准方法中非常重要的一类，它无需提取图像的特征，一旦两幅图像已经配准，它们的互信息即可达到最大值，这是互信息可用于图像配准的理论依据［13～14］。

在粗配准算法中，采用一种基于互信息的优化蚁群算法，具体实现步骤如下：

1）令迭代次数count1=0，设置算法参数及解空间分区数的初值，对搜索空间分区，将m只蚂蚁随机放置于初始区域上。

2）每只蚂蚁以式（4）和（5）给出的概率规则转移或作局部搜索。

3）存储各区域当前已搜索的目标函数最大值。

4）记录当前最好解max x及最优值max f。

5）更新各区域的吸引强度j，count1=count1+1。

6）若count1小于最大迭代次数count1max，则转到步骤2），否则算法结束，输出最佳结果。

根据经验，算法中主要参数的常规设置为1≤α≤5，1≤β≤5，0.5≤ρ≤1；1≤Q≤10000，Q的取值对算法影响不大；蚂蚁数目m和解空间的分区数有关，分区数越大则蚂蚁数目越多，若问题的局部最优点较为密集，则可适当设置较小的区域宽度；最大迭代次数count1max也与分区数有关，分区数越多，最大迭代次数的值也越大。

3 基于纹理特征的细配准

3.1 线性递减权重

设待配准的参考图像和浮动图像分别为Iref和Iflo，对应的参考点集和浮动点集分别为X={x1，x2，…，xn}和Y={y1，y2，…，ym}。当两个点集经过粗配准后，点集X和Y间存在邻近对应关系。假设点集Y的特征点yi在点集X中对应的最近点为xj，那么C(xj)即为yi的邻近点集合。在邻近点集合C(xj)中搜索yi的匹配点，可以大大减少计算耗时，降低配准误差。

把纹理特征加入到距离度量函数中，得到相应的距离度量目标函数为

式中，d1是点对的欧式距离；d2是点对的纹理特征相似性距离，简称纹理距离；N(·)是归一化函数；w是权重参数，0≤w≤1，w取值不同，得到的匹配点集也不同。w越大，ICP算法在搜索点对时越倾向几何距离近的点，w越小，ICP算法越会率先匹配纹理特征相近的点。当w=1时，算法即为传统的ICP算法。

在细配准阶段，初始时权重参数w的值较大，此时几何距离较近的点对率先配准。后面随着迭代次数的增加，w值逐渐减小，降低了几何距离对搜索点的限制，使得纹理特征相近的点对最到匹配，由此实现图像的精确配准。

这里采用线性变化的方式让权重从最大值wmax减小到最小值wmin，权重参数w随迭代次数的变化式为

式中，count2表示当前迭代次数，count2max表示最大迭代次数。

3.2 基于纹理特征的ICP算法

本文利用Gabor小波提取图像的纹理特征，并采用活动表现模型（Active Appearance Model，AAM）算法统计分析样本集中各特征点的纹理显著性［15］。纹理信息tex(x，y)的计算式为

式中，GTf，θ(x，y)表示Gabor核函数与图像的卷积。

基于纹理特征的配准方法是在ICP算法的基础上，通过对纹理特征点赋予权重实现的。对纹理特征显著的特征点赋予较大的权重，反之，赋予较小的权重。通过对图像加入纹理特征，不仅在几何外形上可以实现点对匹配，也可以使得匹配的点对在图像的纹理细节上相似，因此算法的优化目标可表示为

由于图像的旋转和平移变换并不会对特征点的纹理信息产生明显的影响，因此优化目标函数式（9）可简化为

由于目标函数式（10）与传统ICP算法求解优化目标类似，因此采用奇异值分解法求解旋转矩阵和平移矢量。

基于以上目标函数，基于纹理特征的配准算法的步骤如下：

1）对参考图像Iref和浮动图像Iflo，首先采用Snake算法［16］获取图像的边缘轮廓，并将廓边缘离散化。

2）对离散边缘点均匀采样，得到参考点集和浮动点集分别为X={xj，j=1，2，…，n}和Y={yi，i=1，2，…，m}。

3）采用第二部分的改进蚁群算法实现参考图像和浮动图像的粗配准。

4）计算参考点集与浮动点集的纹理信息以及参考图像与浮动图像特征点处的纹理显著性，实现显著纹理特征建模。

5）取浮动点集Y中的一个特征点yi，计算其邻近集合C(xj)中距离最小的点，求解旋转矩阵Rk和平移矢量tk，其中k为迭代次数。

6）计算Yk=RkY+tk，即浮动点集Y经过一次坐标变换后得到数据点集Yk。

7）重复步骤5）到6），直到达到最大迭代次数或者满足下列条件：

8）根据旋转平移变换矩阵对参考图像和浮动图像进行空间变换，得到最终配准结果，算法结束。

4 实验结果与分析

实验选取两幅人脑的CT图像进行配准，如图1所示。其中，图1（a）为参考图像，图1（b）为浮动图像。显然，两幅图像在大小和质量上均存在一定程度的差异。采用基于纹理特征的层次化图像配准方法，首先采用基于互信息的改进蚁群算法实现图像粗配准，然后采用基于纹理特征的ICP算法实现图像细配准，最终配准结果如图2所示。

图1 待配准图像

图2 图像配准结果

实验中，粗配准阶段的参数设置为：蚂蚁数目m=15，信息素的重要程度α=3，启发式因子的重要程度β=3，路径上信息素的蒸发系数ρ=0.8，正常数Q=6000，最大迭代次数count1max=400；细配准阶段的参数设置为：最大迭代次数count2max=300。

为了验证该基于纹理特征的层次化图像配准方法的有效性，实验再分别单独采用本文的粗配准算法（基于互信息的蚁群配准算法）和细配准算法（基于纹理特征的ICP算法）以及文献［17］方法和文献［18］方法等方法对图1（a）和图1（b）的两幅图像进行配准，配准结果如表1所示。

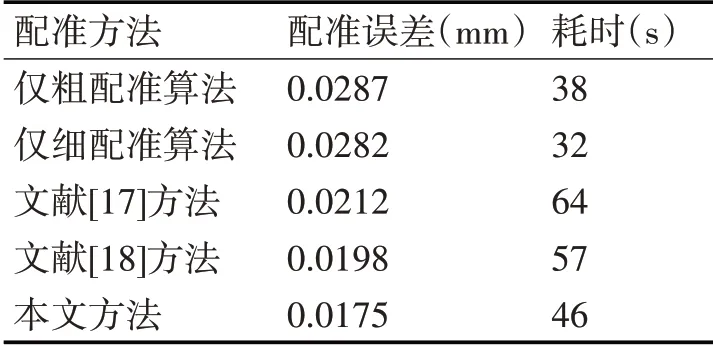
表1 五种方法的配准结果

从表1的配准结果可见，本文提出的配准方法具有最高的配准精度和最快的配准速度，而单独使用本文的粗配准算法或者细配准算法，均会造成较大的配准误差，不能实现图像的精确配准。与文献［17］的配准方法相比，本文算法的配准精度和速度分别提高了约18%和28%；与文献［18］的配准方法相比，本文方法的配准精度和速度分别提高了约11%和19%。因此说，本文配准方法是一种精度高、速度快的图像配准方法，可以实现不同大小和质量图像的精确配准。

5 结语

图像配准技术研究已久，其配准的高精度、快速以及强鲁棒性一直都是该领域所追求的目标。为了实现不同大小和质量的纹理图像的快速精确配准，本文提出一种基于纹理特征的层次化图像配准方法。配准过程分为粗配准和细配准两个阶段，粗配准采用基于互信息的优化蚁群算法实现图像的初始配准，细配准采用基于纹理特征的改进ICP算法实现图像的最终精确配准。该方法可以防止算法陷入局部最优解，加快迭代速度，适用于存在局部形变的纹理图像的配准。当然该方法也具有一定的局限性，如对整体变形较大的图像的配准效果不佳，未考虑大量噪声对配准结果的影响等。在今后的研究中，要综合考虑大形变、噪声等多种因素的影响，提出更加快速、精确、鲁棒的图像配准方法。