网收敛在刻画拓扑空间中重要概念的作用分析

田俊英

(长治学院 沁县师范分院，山西 长治 046400)

0 引言

众所周知，拓扑学中点列的收敛在描述度量空间许多重要的概念有不可或缺的作用。反映这些作用的方法在第一可数空间中得到了推广和实现，例如聚点、闭包、开集、连续等都可以以序列收敛为出发点来刻画。但是在非第一可数空间的背景下，一般的拓扑空间中，不能像上述一样通过序列收敛的性质来刻画聚点，也就没法用序列收敛来刻画闭包、连续等重要概念。在这里，序列收敛的作用就不充分了，就需要将序列收敛进行推广。网是序列概念的一般化，自然地想到尝试用网收敛来实现各种刻画。本文旨在挖掘网收敛对于刻画拓扑空间基本概念的作用，进而为实现网收敛和拓扑的等价地位打好基础。

1 预备知识

定义1[1]设X是一个集合,F是X的一列子集，若F满足如下条件：

(1)X,Ø∈F；

(2)若A,B∈F,则A∩B∈F;

(3)若F1⊂F,则∪A∈F1A∈F,

则称偶对(X,F)是一个拓扑空间，F是集合X的一个拓扑。

定义2[1]有序集(D,≤)称为定向集(directed set),当且仅当对于任意α,β∈D,有γ∈D使α≤γ,β≤γ。

定义3[1]定向集(D,≤)的子集A是共尾的(cofinal),当且仅当对于任意的α∈D,有α1∈A使α≤α1。

定义4[1]定向集(D,≤)的子集A是等终的(eventially),当且仅当有α0∈D,若α≥α0，α∈D时,α∈A。

引理1[2]定向集的等终子集是共尾子集。

引理2[2]A是定向集(D,≤)的共尾子集,即A是D的子有序集，则A也是定向集。

引理3[2]设定向集D=A1∪A2,若A1不是等终的,则A2是共尾的。若A1不是共尾的,则A2是等终的。特别地,A1,A2中至少有一个是共尾的。

由于序列收敛只有在拓扑空间中满足第一可数性公理时才有完整作用,条件比较苛刻。网收敛是序列收敛的推广形式,故在一般拓扑中引进了如下网的概念。

定义5[2]设Y为集合,(D,≤)为定向集,以α∈D为下标的Y的点Sα的全体{Sα:α∈D}，称为(Y的)网(net),简记作{Sα:α∈D,≤}或S。

设X是拓扑空间,X的网{Sα:α∈D,≤}收敛于X中的点x0,等价于对于任意U⊂A(x0),存在α0∈D，当α≥α0,有Sα∈U，即S(D(α0))⊂U。

网的概念是序列概念的一般化。特别地,当D=N(N为自然数集)时,网就是通常的序列。

网{Sα:α∈D,≤}终于A,当且仅当有α0∈D，当α≥α0,α∈D时,有Sα∈A。

网{Sα:α∈D,≤}经常在A中,当且仅当对于D中的每个α,有β∈D,使β≥α,Sβ∈A。

若拓扑空间X中有网{Sα:α∈D,≤},对于任意的α∈D,有Sα=x,称Sα为X中的常值网。

定义6[1]设X是一个拓扑空间,A⊂X,U是点x的任意一个邻域，存在x0∈U,且x0≠x,即U∩(A-{x}≠∅),则称点x是集合A的聚点(也称为极限点)。将A的全部聚点组成的集合称为A的导集,记作d(A)或limA。

定义7[1]设X是一个拓扑空间,A⊂X,若x∈d(A)，有x∈A,即d(A)⊂A,则称A是拓扑空间X中的闭集。

定义9[1]设X是一个拓扑空间,A⊂X，如果A是点x∈A的一邻域,即存在开集V使得x∈V⊂A,则称点x是A的内点。集合A的全部内点组成的集合称为集合A的内部，记作Ao。

定义10[1]设X是一个拓扑空间,A⊂X,U⊂X,如果A⊂Uo,则称集合U是集合A的一个邻域。集合A的全部邻域组成的集合称为A的邻域系,记作A(A)。

定义11[1]设X,Y是两个拓扑空间,f:X→Y，任取U⊂Y,且U为开集，其原像f-1(U)⊂X，且为开集,则称映射f:X→Y连续。

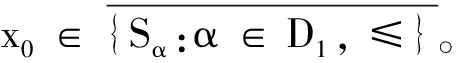
2 主要结果

定理1(刻画聚点)设X是一个拓扑空间,A⊂X,x0∈X,x0是A的聚点,当且仅当在A(x0}上有网S收敛于x0。

证明设x0是A的聚点,则对于x0的任一邻域U,必有点xu∈U∩A,xu≠x0,由于x0的邻域系A(x0)按关系“⊂”是定向集,于是作成网{xU,U⊂A(x0),⊂}收敛于x0。

中国积极顺应全球产业分工不断深化的大趋势,充分发挥比较优势,承接国际产业转移,实施出口拉动外向型经济,大力发展对外贸易和积极促进双向投资,开放型经济实现迅猛发展,综合国力不断增强。汽车产业等资本和技术密集型产业在居民消费结构升级的促进作用下实现快速发展,成为中国重要的支柱产业,并带动了相关产业的发展。

若在A/{x0}上有网S收敛于x0,则由网收敛的定义,知S终于x0的每一个F邻域,故x0的每个邻域中必有异于x0的S的点,即x0的每一个邻域U,必有U∩S≠∅。而U∩S⊂U∩A(x0},故x0是A的聚点。

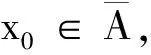
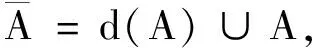
定理3(刻画闭集)设X是一个拓扑空间,A⊂X,且A是闭集,当且仅当对A中任一网S,均有limS∈A。

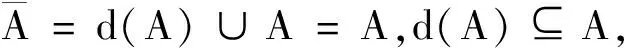
定理4[4](刻画开集)设X是一个拓扑空间,A⊂X,且A是开集，当且仅当对于任意收敛于A内点的网终于A(或者说A中的任意点x0和收敛于x0的任意网{Sα:α∈D,≤},必有{Sα:α∈D,≤}∩A≠∅。

证明设A为开集,由网收敛于一点的定义,若一个网收敛于A内的点, 故其终于A。

假设A不是X的开集,则XA不是闭集,由定理3知,XA中存在网Sα,limSαXA,即limSα∈A。显然,{Sα}是收敛于A内点的网,但是该网不终于A,与条件矛盾。

定理5(刻画连续)设X、Y为拓扑空间,映射f:X→Y连续,当且仅当在X中,若{Sα:α∈D,≤}收敛于x0,则在Y中{f(Sα):α∈D,≤}收敛于f(x0)。

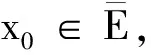
3 结语

对一般的拓扑空间，当序列收敛不充分时，用其推广形式——网收敛，对拓扑空间中的一些相关概念(聚点、闭包、闭集、开集以及连续)进行了完整刻画。在上面的论述中,可以看到,用网收敛可以刻画拓扑学的许多结果，在拓扑空间中，网收敛和拓扑的地位是等价的。事实上，Kelley在他的专著中介绍了任意论域上的拓扑都可以用基于网的收敛类来导出的重要结果。只是习惯了平时所说的拓扑,而且用不同的方法，其描述问题的复杂程度不同而已。其实，尝试用不同的视角来刻画拓扑空间，会发现拓扑空间中看似不相关的内容，实则联系紧密。因此，网收敛还可以进一步刻画分离公理。网收敛如何对分离公理以及正规、正则空间进行刻画，值得进一步分析研究。