Lévy稳定过程均值变点监测在GEWMA和GLR控制图中的对比

胡松瀛,李 泰

(亳州学院 电子与信息工程系，安徽 亳州 236800)

变点问题是统计学中非常热门的一个课题，研究变点问题的一个重要工具是控制图，比较常见的控制图有累计和控制图CUSUM[1]、累积分控制图Cusore[2]、广义似然比控制图GLR[3]、广义指数加权移动平均控制图GEWMA[4]等。常用平均运行长度ARL来对比不同控制图的监测结果。现实中,很多随机变量是服从稳定分布的,有无限方差,被称为Lévy稳定过程。首先给出了GEWMA和GLR控制图监测Lévy稳定过程均值变点ARL的区间估计，然后对监测的效果进行了数值模拟比较。

1 预备知识

引理1[5]相互独立的随机变量Wi,Wi～Sλ(ai,bi,μi),i=1,2,则

W1+W2～Sλ(a,b,μ)

(1)

引理2[5]随机变量W～Sλ(a,b,μ),d是实常数，则

S+d～Sλ(a,b,μ+d)

(2)

引理3[5]随机变量W～Sλ(a,b,μ),实常数d≠0,则

dW～

{Sλ(|d|a,sign(d)b,dμ)λ≠1，

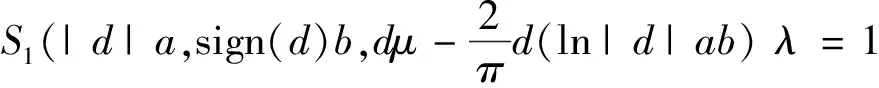
(3)

引理4[5]随机变量W～Sλ(a,b,μ),0<λ<2,则

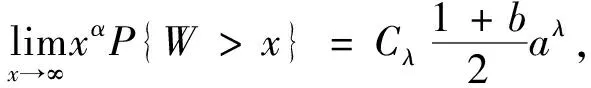
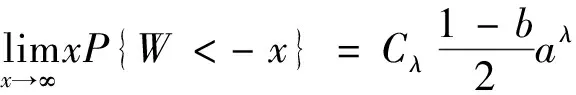
(4)

其中

2 平均运行长度ARL的估计

随机变量W1,W2,…,Wn是独立稳定的,检验问题:

H0:Xi～Sλ(a,b,μ0),i=1,2,…,m

H1:Xi～Sλ(a,b,μ0),i=1,2,…,δ-1

Xi～Sλ(a,b,μ),i=δ,δ+1,…,m

(5)

其中,变点δ未知,μ0≠μ，λ∈(0,2]，b∈[-1,1]，a≥0。

假设检验(5)是对过程均值是否有变点进行检验，没有变点接受H0,有变点接受H1。从时刻δ开始，均值发生μ-μ0的变化。μ>μ0时为向上漂移，μ<μ0时为向下漂移。不论是向下漂移,还是向上漂移,监测的方法上没有实质区别，故只讨论向上漂移的监测并且假设μ0=0，a=1，b=0，δ=1。另外设ARL0是受控平均运行长度,ARLμ是失控平均运行长度,

ARL0(T)=E(T)ARLμ(T)=Eμ(T)

其中T是过程失控预警的时间。考虑到实际情况,求出控制极限c充分大时控制图的平均运行长度ARL的估计。

定理1稳定过程的第i个观测值Wi～Sλ(1,0,μi),i=1,2,…，且相互独立，设μ0=inf[μi],μ0=sup[μi]，其中1<λ≤2，μi≥0，那么对于GEWMA控制图

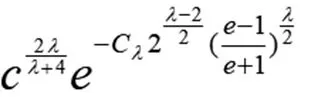
(6)

证明由于

得

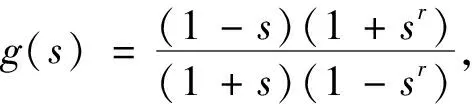
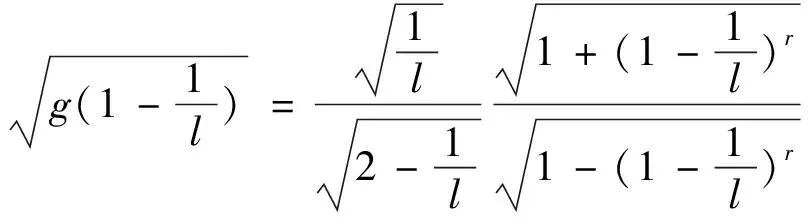
所以当0≤s<1时，有g′(s)≤0，因此当l≤n0时，有

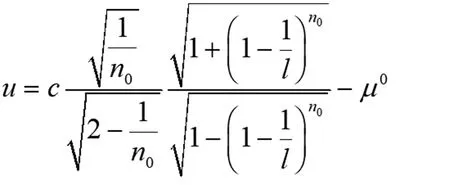
那么

因而

定理2稳定过程的第i个观测值Wi～Sλ(1,0,μi),i=1,2,…,且相互独立，设μ0=inf[μi],μ0=sup[μi]，其中1<λ≤2，μi≥0，对于GLR控制图,有

(1+o(1))c2λ/(6-λ)e-Cλ/4≤ARLμi(TGL)

≤(c2/μ02+cb/μ0)(1+o(1))

(7)

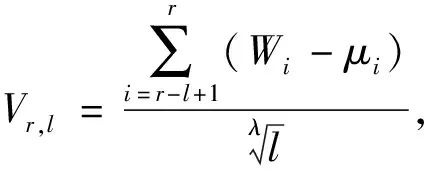
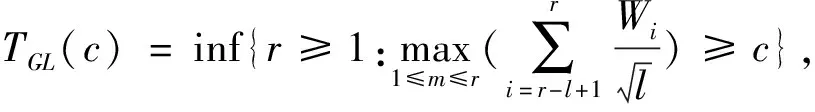
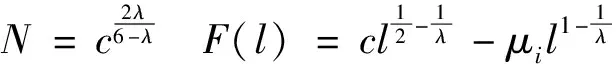
故当1≤l≤N，F(l)在N处取得最小值，那么

(7)式的向下不等式得证。

设M(c)=c2/μ02+cb/μ0，Mi=M(c)i，i≥0

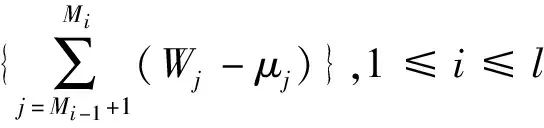
因为

(7)式的向上不等式得证。

3 数值模拟

在ARL0相等的条件下取定μ，然后比较ARLμ，ARLμ越小说明这种控制图的效果就越好。表1、表2是GEWMA和GLR这两种控制图监测向上漂移的模拟结果。首先设时间序列服从Sλi(1,0,μ)，其中αi∈(1,2]，然后运用rstalbe程序生成随机变量序列Wi～Sλi(1,0,μ)，τ=1，模拟结果是由10000次重复实验得出。

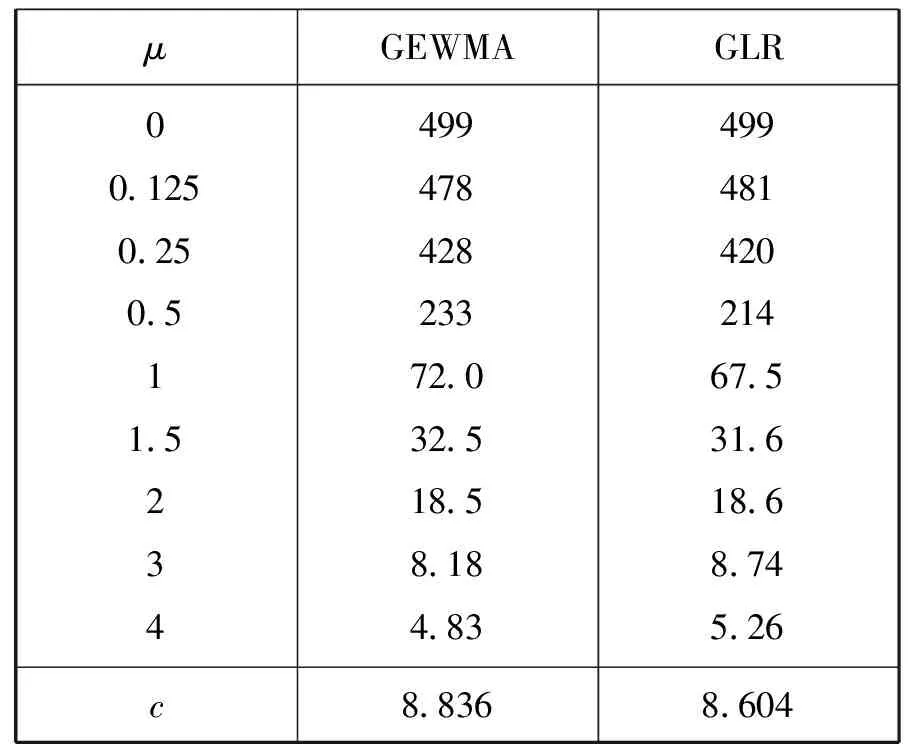
表1 Wi～S1.8(1,0,μ)

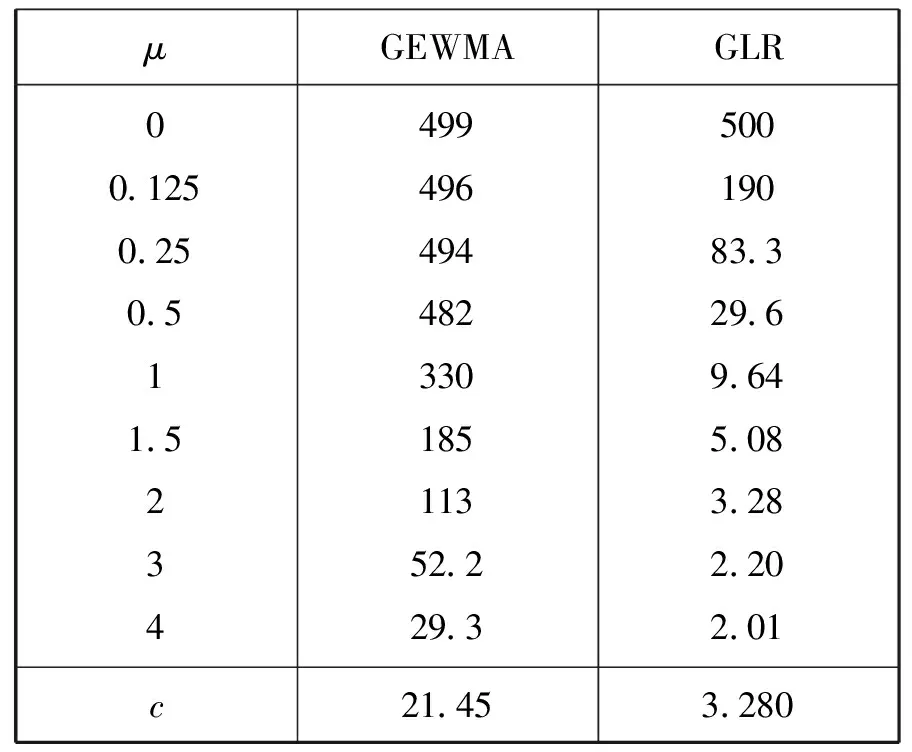
表2 Wi～S1.5(1,0,μ)

4 数据分析

通过对比，可以得到，如果λ=1.5，这时控制图GLR的效果优于GEWMA，如果λ=1.8，两种控制图效果不相上下。